Богосорт

Богосорт

Сорт	Сортировка
Структура данных	Множество
Худшая производительность	Неограниченный (рандомизированная версия), $O(n\times n!)$ (детерминированная версия)
Лучшая производительность	$\Omega (n)$
Средняя производительность	$\Theta (n\times n!)$
Наихудшая пространственная сложность	$\mathrm {O} (1)$

В информатике , богосорт (также известная как сортировка перестановками и глупая сортировка) ) — это алгоритм сортировки, основанный на парадигме генерации и тестирования . Функция последовательно генерирует перестановки своих входных данных, пока не найдет ту, которая отсортирована. Он не считается полезным для сортировки, но может использоваться в образовательных целях, чтобы противопоставить его более эффективным алгоритмам.

Существуют две версии этого алгоритма: детерминированная версия, которая перечисляет все перестановки, пока не достигнет отсортированной, и рандомизированная версия, которая случайным образом меняет входные данные. Аналогией работы последней версии является сортировка колоды карт, подбрасывая колоду в воздух, собирая карты в случайном порядке и повторяя процесс, пока колода не будет отсортирована. В худшем случае с этой версией случайный источник имеет низкое качество и делает отсортированную перестановку неограниченно маловероятной. Название алгоритма представляет собой сочетание слов bogus и sort .

Описание алгоритма

Псевдокод

Ниже приводится описание рандомизированного алгоритма в псевдокоде :

while not sorted(deck):
    shuffle(deck)

С

Вот реализация на C:

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

// executes in-place bogo sort on a given array
static void bogo_sort(int* a, int size);
// returns 1 if given array is sorted and 0 otherwise
static int is_sorted(int* a, int size);
// shuffles the given array into a random order
static void shuffle(int* a, int size);

void bogo_sort(int* a, int size) {
    while (!is_sorted(a, size)) {
        shuffle(a, size);
    }
}

int is_sorted(int* a, int size) {
    for (int i = 0; i < size-1; i++) {
        if (a[i] > a[i+1]) {
            return 0;
        }
    }
    return 1;
}

void shuffle(int* a, int size) {
    int temp, random;
    for (int i = 0; i < size; i++) {
        random = (int) ((double) rand() / ((double) RAND_MAX + 1) * size);
        temp = a[random];
        a[random] = a[i];
        a[i] = temp;
    }
}

int main() {
    // example usage
    int input[] = { 68, 14, 78, 98, 67, 89, 45, 90, 87, 78, 65, 74 };
    int size = sizeof(input) / sizeof(*input);

    // initialize pseudo-random number generator
    srand(time(NULL));

    bogo_sort(input, size);

    // sorted result: 14 45 65 67 68 74 78 78 87 89 90 98
    printf("sorted result:");
    for (int i = 0; i < size; i++) {
        printf(" %d", input[i]);
    }
    printf("\n");

    return 0;
}

Питон

Вот приведенный выше псевдокод, переписанный на Python 3 :

import random

# bogosort
# what happens is there is a random array that is generated by the last function
# the first function checks whether the array is sorted or not
# the second function repeatedly shuffles the array for as long as it remains unsorted
# and that's it
# happy coding =>

# this function checks whether or not the array is sorted
def is_sorted(random_array):
  for i in range(1, len(random_array)):
    if random_array[i] < random_array[i - 1]:
      return False
  return True

# this function repeatedly shuffles the elements of the array until they are sorted
def bogo_sort(random_array):
  while not is_sorted(random_array):
    random.shuffle(random_array)
  return random_array

# this function generates an array with randomly chosen integer values
def generate_random_array(size, min_val, max_val):
  return [random.randint(min_val, max_val) for _ in range(size)]

# the size, minimum value and maximum value of the randomly generated array
size = 10
min_val = 1
max_val = 100
random_array = generate_random_array(size, min_val, max_val)
print("Unsorted array:", random_array)
sorted_arr = bogo_sort(random_array)
print("Sorted array:", sorted_arr)

Этот код предполагает, что data — это простая, изменяемая, подобная массиву структура данных, подобная встроенной в Python list— элементы которого можно без проблем сравнивать.

Время работы и прекращение действия

Экспериментальная среда выполнения bogosort

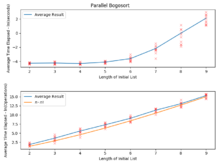
Если все элементы, подлежащие сортировке, различны, ожидаемое количество сравнений, выполняемых в среднем случае с помощью рандомизированной богосортии, асимптотически эквивалентно ( e − 1) n ! , а ожидаемое количество свопов в среднем случае равно ( n − 1) n ! . Ожидаемое количество свопов растет быстрее, чем ожидаемое количество сравнений, поскольку, если элементы не в порядке, это обычно обнаруживается всего лишь после нескольких сравнений, независимо от того, сколько элементов имеется; но работа по перетасовке коллекции пропорциональна ее размеру. В худшем случае количество сравнений и перестановок не ограничено по той же причине, по которой на брошенной монете может выпасть решка любое количество раз подряд.

В лучшем случае это произойдет, если указанный список уже отсортирован; в этом случае ожидаемое количество сравнений равно n − 1 , и никакие замены вообще не выполняются.

Для любой коллекции фиксированного размера ожидаемое время работы алгоритма конечно по той же причине, по которой справедлива теорема о бесконечных обезьянах : существует некоторая вероятность получения правильной перестановки, поэтому, учитывая неограниченное количество попыток, она почти наверняка в конечном итоге произойдет. быть выбранным.

Связанные алгоритмы

Горосорт

Алгоритм сортировки, представленный на Google Code Jam 2011 года . Пока список не в порядке, подмножество всех элементов переставляется случайным образом. Если это подмножество выбирается оптимально каждый раз, когда это выполняется, ожидаемое значение общего количества раз, которое необходимо выполнить эту операцию, равно количеству неуместных элементов.

Богобогосорт

Алгоритм, который рекурсивно вызывает себя с все меньшими и меньшими копиями начала списка, чтобы проверить, отсортированы ли они. Базовый случай — это один элемент, который всегда отсортирован. В других случаях он сравнивает последний элемент с максимальным элементом из предыдущих элементов в списке. Если последний элемент больше или равен, он проверяет, соответствует ли порядок копии предыдущей версии, и если да, то возвращает результат. В противном случае он перетасовывает текущую копию списка и перезапускает рекурсивную проверку.

Бозосорт

Еще один алгоритм сортировки, основанный на случайных числах. Если список не в порядке, он выбирает два элемента случайным образом и меняет их местами, а затем проверяет, отсортирован ли список. Анализ времени выполнения бозосорта более сложен, но некоторые оценки можно найти в анализе Х. Грубера «извращенно ужасных» алгоритмов рандомизированной сортировки. O( n !) оказывается ожидаемым средним случаем.

Худший сорт

Алгоритм пессимальной сортировки, который гарантированно завершается за конечное время; однако его эффективность может быть сколь угодно низкой, в зависимости от его конфигурации. Алгоритм худшей сортировки основан на алгоритме плохой сортировки badsort . Алгоритм плохой сортировки принимает два параметра: L — список для сортировки и k — глубина рекурсии. На уровне рекурсии k = 0 badsort просто использует общий алгоритм сортировки, такой как пузырьковая сортировка , для сортировки входных данных и возврата отсортированного списка. То есть badsort( L , 0) = bubblesort( L ) . Следовательно, временная сложность бадсортировки равна O( n ² ), если k = 0 . Однако для любого k > 0 badsort ( L , k ) сначала генерирует P , список всех перестановок L . Затем badsort вычисляет badsort( P , k − 1) и возвращает первый элемент отсортированного P . Чтобы сделать наихудшую сортировку действительно пессимальной, k можно присвоить значению вычислимой возрастающей функции, такой как $f\colon \mathbb {N} \to \mathbb {N}$ (например, f ( n ) = A ( n , n ) , где A — функция Аккермана ). Следовательно, чтобы отсортировать список сколь угодно плохо, можно было бы выполнить наихудшую сортировку( L , f ) = badsort( L , f (length( L ))) , где length( L ) — количество элементов в L . Полученный алгоритм имеет сложность ${\textstyle \Omega \left(\left(n!^{(f(n))}\right)^{2}\right)}$, где $n!^{(m)}=(\dotso ((n!)!)!\dotso )!$ = факториал n, повторенный m раз. Этот алгоритм можно сделать сколь угодно неэффективным, выбрав достаточно быстро растущую функцию f .

медленная сортировка

Другой юмористический алгоритм сортировки, который использует ошибочную стратегию «разделяй и властвуй» для достижения огромной сложности.

Квантовая богосортировка

Гипотетический алгоритм сортировки, основанный на богосортировке, созданный в шутку среди ученых-компьютерщиков. Алгоритм генерирует случайную перестановку входных данных, используя квантовый источник энтропии, проверяет, отсортирован ли список, и, если это не так, уничтожает вселенную. Если предположить, что интерпретация многих миров верна, использование этого алгоритма приведет к тому, что по крайней мере одна сохранившаяся вселенная будет успешно отсортирована за время O( n ) .

Чудо сортировка

Алгоритм сортировки, который проверяет, отсортирован ли массив, пока не произойдет чудо . Он постоянно проверяет массив, пока он не будет отсортирован, никогда не меняя порядок массива. Поскольку порядок никогда не изменяется, алгоритм имеет гипотетическую временную сложность O ( ∞ ) , но он все равно может сортировать такие события, как чудеса или единичные сбои . При реализации этого алгоритма необходимо проявлять особую осторожность, поскольку оптимизирующие компиляторы могут просто преобразовать его в цикл while(true) . Однако лучший случай — O ( n ) , который происходит в отсортированном списке. Поскольку он только сравнивает, он строго уместен и стабилен.

См. также

• алгоритм Лас-Вегаса
• марионетка сортировка

Внешние ссылки

• BogoSort на WikiWikiWeb
• Неэффективные алгоритмы сортировки
• Bogosort : реализация, работающая в Unix-подобных системах, аналогичная стандартной программе сортировки .
• Богосорт и jmmcg::bogosort : Простая, но извращенная реализация алгоритма богосорта на C++.
• Пакет Bogosort NPM : реализация bogosort для экосистемы Node.js.
• Макс Шерман «Бого-сорт вроде медленный» , июнь 2013 г.