Лемма о восходящем солнце

Иллюстрация, поясняющая, почему эта лемма называется «Лемма о восходящем солнце».

В математическом анализе лемма о восходящем солнце — лемма Фридьеса Рисса , использованная при доказательстве максимальной теоремы Харди-Литтлвуда . Лемма была предшественником в одном измерении леммы Кальдерона-Зигмунда .

Лемма формулируется следующим образом:

Предположим, что g — непрерывная функция с действительным знаком на интервале [ a , b ], а S — множество x в [ a , b ] такое, что существует y ∈( x , b ] с g ( y ) > g ( x ). (Обратите внимание, что b не может находиться в S , хотя a может быть.) Определим E = S ∩ ( a , b ).

Тогда E — открытое множество, и его можно записать как счетное объединение непересекающихся интервалов.

$E=\bigcup _{k}(a_{k},b_{k})$

такой, что g ( a _k ) = g ( b _k ), если только a _k = a ∈ S для некоторого k , и в этом случае g ( a ) < g ( b _k ) для этого k . того, если x ∈ ( , _g bk ) ₍ , то g ( x ) < ) bk Более _ak .

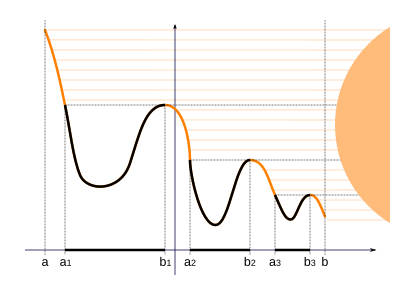
Красочное название леммы связано с представлением графика функции g в виде горного ландшафта. Солнце светит горизонтально справа. Множество E состоит из точек, находящихся в тени.

Доказательство

Нам понадобится лемма: пусть [ c , d ) ⊂ S , но d S. ∉ Тогда g ( c ) < g ( d ).Чтобы доказать это, предположим, что g ( c ) ≥ g ( d ).Тогда g достигает максимума на [ c , d ] в некоторой точке z < d .Поскольку z ∈ S , существует y в ( z , b ] такой, что g ( z ) < g ( y ). Если y ≤ d , то g не достигнет своего максимума на [ c , d ] в точке z .Таким образом, y ∈ ( d , b ] и g ( d ) ≤ g ( z ) < g ( y ).Это означает, что d ∈ S , что противоречит, что и доказывает лемму.

Множество E открыто, поэтому оно состоит из счетного объединения непересекающихся интервалов , ₍ bk ) _ak .

Из леммы сразу следует, что g ( x ) < g ( bk ₎ для x в ( а _к , б _к ).Поскольку g непрерывен, мы также должны иметь g ( a _k ) ⩽ g ( b _k ).

Если ak _a ≠ a или S ∉ S то a _k ∉ , , поэтому g ( a _k ) ≥ g ( b _k ), иначе a _k ∈ S . Таким образом, в этих случаях g ( a _k ) = g ( b _k ).

Наконец, если a _k = a ∈ S , лемма говорит нам, что g ( a ) < g ( b _k ).

Ссылки

• Дюрен, Питер Л. (2000), Теория H ^п Пространства , Нью-Йорк: Dover Publications, ISBN  0-486-41184-2
• Гарлинг, DJH (2007), Неравенства: путешествие в линейный анализ , Cambridge University Press, ISBN  978-0-521-69973-0
• Кореновский А.А.; А.К. Лернер; А. М. Стоколос (ноябрь 2004 г.), «О многомерной форме леммы Ф. Рисса о восходящем солнце», Proceedings of the American Mathematical Society , 133 (5): 1437–1440, doi : 10.1090/S0002-9939-04-07653 -1
• Рис, Фредерик (1932), «Sur un Théorème de Maximum de Mm. Hardy et Littlewood» , Журнал Лондонского математического общества , 7 (1): 10–13, doi : 10.1112/jlms/s1-7.1.10 , в архиве из оригинала от 15 апреля 2013 г. , получено 21 июля 2008 г.
• Стейн, Элиас (1998), «Сингулярные интегралы: роли Кальдерона и Зигмунда» (PDF) , Уведомления Американского математического общества , 45 (9): 1130–1140 .
• Тао, Теренс (2011), Введение в теорию меры , Аспирантура по математике , том. 126, Американское математическое общество, ISBN.  978-0821869192
• Зигмунд, Антони (1977), Тригонометрический ряд. Том. I, II (2-е изд.), Издательство Кембриджского университета, ISBN  0-521-07477-0