Выборка обратного преобразования

Выборка с обратным преобразованием (также известная как инверсионная выборка , обратное интегральное преобразование вероятности , метод обратного преобразования или Смирнова преобразование ) — это базовый метод выборки псевдослучайных чисел генерации чисел выборки , т. е. для случайной из любого распределения вероятностей заданного . его кумулятивная функция распределения .

Выборка обратного преобразования берет однородные выборки числа. $u$ между 0 и 1, интерпретируется как вероятность, а затем возвращает наименьшее число $x\in \mathbb {R}$ такой, что $F(x)\geq u$ для кумулятивной функции распределения $F$ случайной величины. Например, представьте, что $F$ — стандартное нормальное распределение с нулевым средним значением и единицей стандартного отклонения. В таблице ниже показаны выборки, взятые из равномерного распределения, и их представление в стандартном нормальном распределении.

Преобразование однородной выборки в нормальную

$u$	$F^{-1}(u)$
.5	0
.975	1.95996
.995	2.5758
.999999	4.75342
1-2 −52	8.12589

Выборка обратного преобразования для нормального распределения

Мы случайным образом выбираем долю площади под кривой и возвращаем число в области определения так, чтобы именно эта доля площади находилась слева от этого числа. Интуитивно мы вряд ли выберем число в дальнем конце хвостов, потому что в них очень маленькая область, которая потребует выбора числа, очень близкого к нулю или единице.

В вычислительном отношении этот метод включает в себя вычисление функции квантиля распределения — другими словами, вычисление кумулятивной функции распределения (CDF) распределения (которая сопоставляет число в области значений с вероятностью от 0 до 1), а затем инвертирование этой функции. Это источник термина «инверсия» или «инверсия» в большинстве названий этого метода. Обратите внимание, что для дискретного распределения вычисление CDF, как правило, не слишком сложно: мы просто складываем отдельные вероятности для различных точек распределения. Однако для непрерывного распределения нам необходимо интегрировать функцию плотности вероятности (PDF) распределения, что невозможно сделать аналитически для большинства распределений (включая нормальное распределение ). В результате этот метод может оказаться неэффективным в вычислительном отношении для многих распределений, и другие методы являются предпочтительными; тем не менее, это полезный метод для создания более широко применимых пробоотборников, например, основанных на браковочной выборке. .

Для нормального распределения отсутствие аналитического выражения для соответствующей функции квантиля означает, что другие методы (например, преобразование Бокса-Мюллера ) могут быть предпочтительными в вычислительном отношении. Часто даже для простых распределений метод выборки обратного преобразования можно улучшить: см., например, алгоритм зиккурата и отбраковочную выборку . С другой стороны, можно чрезвычайно точно аппроксимировать функцию квантиля нормального распределения, используя полиномы умеренной степени, и на самом деле метод сделать это достаточно быстрый, поэтому инверсионная выборка теперь является методом по умолчанию для выборки из нормального распределения. в статистическом R. пакете

Официальное заявление

Для любой случайной величины $X\in \mathbb {R}$, случайная величина $F_{X}^{-1}(U)$ имеет то же распределение, что и $X$, где $F_{X}^{-1}$ является обобщенной обратной функцией кумулятивного распределения $F_{X}$ из $X$ и $U$ является однородным на $[0,1]$.

Для непрерывных случайных величин обратное преобразование интеграла вероятности действительно является обратным преобразованию интеграла вероятности , которое утверждает, что для непрерывной случайной величины $X$ с кумулятивной функцией распределения $F_{X}$, случайная величина $U=F_{X}(X)$ является однородным на $[0,1]$.

График техники инверсии из $x$ к $F(x)$. Справа внизу мы видим обычную функцию, а слева вверху — ее инверсию.

Интуиция

От $U\sim \mathrm {Unif} [0,1]$, мы хотим сгенерировать $X$ с CDF $F_{X}(x).$ Мы предполагаем $F_{X}(x)$ быть непрерывной, строго возрастающей функцией, что обеспечивает хорошую интуицию.

Мы хотим посмотреть, сможем ли мы найти какое-нибудь строго монотонное преобразование. $T:[0,1]\mapsto \mathbb {R}$, такой, что $T(U){\overset {d}{=}}X$. у нас будет

$F_{X}(x)=\Pr(X\leq x)=\Pr(T(U)\leq x)=\Pr(U\leq T^{-1}(x))=T^{-1}(x),{\text{ for }}x\in \mathbb {R} ,$

где последний шаг использовал это $\Pr(U\leq y)=y$ когда $U$ является однородным на $[0,1]$.

Итак, мы получили $F_{X}$ быть обратной функцией $T$или, что то же самое $T(u)=F_{X}^{-1}(u),u\in [0,1].$

Следовательно, мы можем генерировать $X$ от $F_{X}^{-1}(U).$

Метод

Схема выборки обратного преобразования. Обратная функция $y=F_{X}(x)$ может быть определен $F_{X}^{-1}(y)=\mathrm {inf} \{x|F_{X}(x)\geq y\}$.

Анимация того, как выборка с обратным преобразованием генерирует нормально распределенные случайные значения из равномерно распределенных случайных значений.

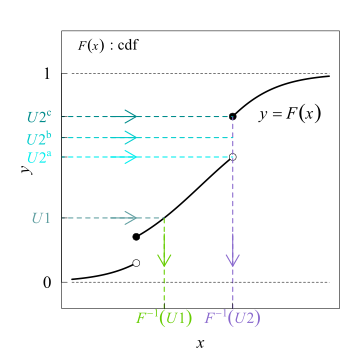
Проблема, которую решает метод выборки обратного преобразования, заключается в следующем:

• Позволять $X$ быть случайной величиной, распределение которой можно описать кумулятивной функцией распределения. $F_{X}$.
• Мы хотим генерировать значения $X$ которые распределяются согласно этому распределению.

Метод выборки обратного преобразования работает следующим образом:

1. Генерировать случайное число $u$ из стандартного равномерного распределения на интервале $[0,1]$, то есть из $U\sim \mathrm {Unif} [0,1].$
2. Найдите обобщенную обратную величину искомого CDF, т.е. $F_{X}^{-1}(u)$.
3. Вычислить $X'(u)=F_{X}^{-1}(u)$. Вычисленная случайная величина $X'(U)$ имеет распространение $F_{X}$ и, следовательно, тот же закон, что и $X$.

Выражается по-другому, учитывая кумулятивную функцию распределения $F_{X}$ и универсальная переменная $U\in [0,1]$, случайная величина $X=F_{X}^{-1}(U)$ имеет распределение $F_{X}$.

В непрерывном случае можно рассматривать такие обратные функции как объекты, удовлетворяющие дифференциальным уравнениям. Некоторые такие дифференциальные уравнения допускают явные решения в виде степенных рядов , несмотря на их нелинейность.

Примеры

• В качестве примера предположим, что у нас есть случайная величина $U\sim \mathrm {Unif} (0,1)$ и кумулятивная функция распределения

${\begin{aligned}F(x)=1-\exp(-{\sqrt {x}})\end{aligned}}$

Чтобы выполнить инверсию, нам нужно найти $F(F^{-1}(u))=u$

${\begin{aligned}F(F^{-1}(u))&=u\\1-\exp \left(-{\sqrt {F^{-1}(u)}}\right)&=u\\F^{-1}(u)&=(-\log(1-u))^{2}\\&=(\log(1-u))^{2}\end{aligned}}$

Отсюда мы выполним шаги первый, второй и третий.

• В качестве другого примера мы используем экспоненциальное распределение с $F_{X}(x)=1-e^{-\lambda x}$ для x ≥ 0 (и 0 в противном случае). Решая y=F(x), мы получаем обратную функцию

$x=F^{-1}(y)=-{\frac {1}{\lambda }}\ln(1-y).$

Это означает, что если мы нарисуем некоторые $y_{0}$из $U\sim \mathrm {Unif} (0,1)$ и вычислить $x_{0}=F_{X}^{-1}(y_{0})=-{\frac {1}{\lambda }}\ln(1-y_{0}),$ Этот $x_{0}$ имеет экспоненциальное распределение.

Идея иллюстрируется следующим графиком:

Случайные числа yi _{генерируются} из равномерного распределения между 0 и 1, т.е. Y ~ U(0, 1). Они изображаются в виде цветных точек на оси Y. Каждая из точек отображается в соответствии с x=F ⁻¹ (y), который показан серыми стрелками для двух примерных точек. В этом примере мы использовали экспоненциальное распределение. Следовательно, при x ≥ 0 плотность вероятности равна $\varrho _{X}(x)=\lambda e^{-\lambda \,x}$ а кумулятивная функция распределения равна $F(x)=1-e^{-\lambda \,x}$. Поэтому, $x=F^{-1}(y)=-{\frac {\ln(1-y)}{\lambda }}$. Мы видим, что при использовании этого метода многие точки оказываются близкими к 0 и только несколько точек имеют высокие значения x — как и ожидается для экспоненциального распределения.

Обратите внимание, что распределение не изменится, если мы начнем с 1-y вместо y. Поэтому для вычислительных целей достаточно сгенерировать случайные числа y в [0, 1], а затем просто вычислить

$x=F^{-1}(y)=-{\frac {1}{\lambda }}\ln(y).$

Доказательство правильности

Позволять $F$ — кумулятивная функция распределения , и пусть $F^{-1}$ быть его обобщенной обратной функцией (с использованием нижней границы , поскольку CDF слабо монотонны и непрерывны справа ):

$F^{-1}(u)=\inf \;\{x\mid F(x)\geq u\}\qquad (0<u<1).$

Претензия: Если $U$ является однородной случайной величиной на $[0,1]$ затем $F^{-1}(U)$ имеет $F$ в качестве CDF.

Доказательство:

${\begin{aligned}&\Pr(F^{-1}(U)\leq x)\\&{}=\Pr(U\leq F(x))\quad &(F{\text{ is right-continuous, so }}\{u:F^{-1}(u)\leq x\}=\{u:u\leq F(x)\})\\&{}=F(x)\quad &({\text{because }}\Pr(U\leq u)=u,{\text{ when }}U{\text{ is uniform on }}[0,1])\\\end{aligned}}$

Усеченное распространение

Выборку обратного преобразования можно просто распространить на случаи усеченных распределений на интервале $(a,b]$ без затрат на отбраковочную выборку: можно следовать тому же алгоритму, но вместо генерации случайного числа $u$ равномерно распределены между 0 и 1, генерируют $u$ равномерно распределены между $F(a)$ и $F(b)$, а затем снова возьмем $F^{-1}(u)$.

Уменьшение количества инверсий

Чтобы получить большое количество выборок, необходимо выполнить такое же количество инверсий распределения. Одним из возможных способов уменьшить количество инверсий при получении большого количества выборок является применение так называемого семплера стохастической коллокации Монте-Карло (семплера SCMC) в рамках структуры полиномиального расширения хаоса . Это позволяет нам генерировать любое количество выборок Монте-Карло лишь с несколькими инверсиями исходного распределения с независимыми выборками переменной, для которой инверсии доступны аналитически, например, стандартной нормальной переменной.

Реализации программного обеспечения

Существуют программные реализации для применения метода обратной выборки с использованием числовых аппроксимаций обратного метода в том случае, если он недоступен в закрытой форме. Например, можно вычислить аппроксимацию обратного результата, если пользователь предоставит некоторую информацию о распределениях, например PDF-файл. или CDF.

• Библиотека C УНУ.РАН
• R библиотека Рунуран
• Выборка подпакета Python в scipy.stats

См. также

• Интегральное преобразование вероятности
• Копула , определяемая посредством преобразования интеграла вероятности.
• Функция квантиля для явного построения обратных CDF.
• Обратная функция распределения для точного математического определения распределений с дискретными компонентами.
• Отбраковочная выборка — еще один распространенный метод генерации случайных переменных, который не основан на инверсии CDF.