Слово без квадратов

В комбинаторике слово без квадратов — это слово (последовательность символов), не содержащее квадратов. Квадрат — это слово формы $XX$ , где $X$ не пусто. Таким образом, слово без квадратов также можно определить как слово, избегающее шаблона $XX$ .

Конечные слова без квадратов

Двоичный алфавит

Над двоичным алфавитом $\{0,1\}$ , единственные слова без квадратов - это пустое слово $\epsilon ,0,1,01,10,010$ , и $101$ .

Троичный алфавит

Над троичным алфавитом $\{0,1,2\}$ , существует бесконечно много слов без квадратов. Можно посчитать количество $c(n)$ троичных слов без квадратов длины $n$ .

Количество троичных слов без квадратов длины n ^[1]
$н$	0	1	2	3	4	5	6	7	8	9	10	11	12
⁠ $c(n)$ ⁠	1	3	6	12	18	30	42	60	78	108	144	204	264

Это число ограничено $c(n)=\Theta (\alpha ^{n})$ , где ${\textstyle 1.3017597<\alpha <1.3017619}$ . ^[2] Верхняя граница на $\alpha$ можно найти с помощью леммы Фекете и аппроксимации автоматами . Нижнюю оценку можно найти, найдя замену, сохраняющую свободу от квадратов. ^[2]

Алфавит с более чем тремя буквами

Поскольку в трехбуквенном алфавите существует бесконечно много слов без квадратов, это означает, что существует также бесконечно много слов без квадратов в алфавите, содержащем более трех букв.

В следующей таблице показана точная скорость роста $k$ -арных слов без квадратов, округленных до 7 цифр после запятой, для $k$ в диапазоне от 4 до 15: ^[2]

Скорость роста $k$ -арных слов без квадратов
размер алфавита ( $к$ )	4	5	6	7	8	9
темп роста	2.6215080	3.7325386	4.7914069	5.8284661	6.8541173	7.8729902
размер алфавита ( $к$ )	10	11	12	13	14	15
темп роста	8.8874856	9.8989813	10.9083279	11.9160804	12.9226167	13.9282035

двумерные слова

Рассмотрим карту ${\textbf {w}}$ от $\mathbb {N} ^{2}$ до $A$ , где $A$ — алфавит и ${\textbf {w}}$ называется двумерным словом. Позволять $w_{m,n}$ быть входом ${\textbf {w}}(m,n)$ . Слово ${\textbf {x}}$ это линия ${\textbf {w}}$ если существует $i_{1},i_{2},j_{1},j_{2}$ такой, что ${\text{gcd}}(j_{1},j_{2})=1$ и для $t\geq 0,x_{t}=w_{{i_{1}}+{j_{1}t},{i_{2}}+{j_{2}t}}$ . ^[3]

Карпи ^[4] доказывает, что существует двумерное слово ${\textbf {w}}$ в 16-буквенном алфавите, в котором каждая строка ${\textbf {w}}$ бесквадратен. Компьютерный поиск показывает, что двумерных слов нет. ${\textbf {w}}$ в семибуквенном алфавите, так что каждая строка ${\textbf {w}}$ бесквадратен.

Генерация конечных слов без квадратов

Шур ^[5] предлагает алгоритм под названием R2F (random-t(w)o-free), который может генерировать слово без квадратов длины $n$ в любом алфавите с тремя или более буквами. Этот алгоритм основан на модификации энтропийного сжатия : он случайным образом выбирает буквы из k-буквенного алфавита для генерации ⁠ $(k+1)$ ⁠ -арное слово без квадратов.

algorithm R2F is
    input: alphabet size  $k\geq 2$ ,
           word length  $n>1$ 
    output: a ⁠ $(k+1)$ ⁠-ary square-free word  $w$ of length  $n$ .

    (Note that  ${\textstyle \color {gray}\Sigma _{k+1}}$  is the alphabet with letters  $\color {gray}\{1,...,k+1\}$ .)
    (For a word  $\color {gray}w\in \Sigma _{k}$ ,  $\color {gray}\chi _{w}$  is the permutation of  $\color {gray}\Sigma _{k}$  such that  $a$  precedes  $b$  in  $\color {gray}\chi _{w}$  if the 
     right most position of  $a$  in  $w$  is to the right of the rightmost position of  $b$  in  $w$ .
     For example,   $\color {gray}w=136263163\in \Sigma _{6}$  has  $\color {gray}\chi _{w}=361245$ .)

    choose  $w[1]$  in  ${\textstyle \Sigma _{k+1}}$  uniformly at random 
    set  $\chi _{w}$  to  $w[1]$  followed by all other letters of  ${\textstyle \Sigma _{k+1}}$  in increasing order
    set the number  $N$  of iterations to 0

    while  $|w|<n$  do
        choose  $j$  in  ${\textstyle \Sigma _{k}}$  uniformly at random
        append  $a=\chi _{w}[j+1]$  to the end of  $w$ 
        update  $\chi _{w}$  shifting the first  $j$  elements to the right and setting  $\chi _{w}[1]=a$ 
        increment  $N$  by  $1$ 
        if  $w$  ends with a square of rank  $r$  then
            delete the last  $r$  letters of  $w$ 

    return  $w$

Каждое (k+1)-арное слово без квадратов может быть результатом алгоритма R2F, поскольку на каждой итерации он может добавлять любую букву, кроме последней буквы слова $w$ .

Ожидаемое количество случайных k-ичных букв, используемых алгоритмом R2F для построения ⁠ $(k+1)$ ⁠ -арное слово без квадратов длины $n$ — это $N=n\left(1+{\frac {2}{k^{2}}}+{\frac {1}{k^{3}}}+{\frac {4}{k^{4}}}+O\left({\frac {1}{k^{5}}}\right)\right)+O(1).$ Обратите внимание, что существует алгоритм, который может проверить отсутствие квадратов слова длины $n$ в $O(n\log n)$ время. Апостольский и подготовленный ^[6] приведите алгоритм с использованием суффиксных деревьев. Крочемор ^[7] использует разделение в своем алгоритме. Майн и Лоренц ^[8] Предложите алгоритм, основанный на методе «разделяй и властвуй». Простая реализация может потребовать $O(n^{2})$ время для проверки отсутствия квадратов слова длины $n$ .

Бесконечные слова без квадратов

с тремя и более буквами существуют бесконечно длинные слова без квадратов В любом алфавите , как доказал Аксель Туэ . ^[9]

Примеры

Первое отличие последовательности Туэ – Морса

Одним из примеров бесконечного слова без квадратов в алфавите размера 3 является слово в алфавите. $\{-1,0,+1\}$ получается путем взятия первой разности последовательности Туэ-Морса . ^[9] То есть из последовательности Туэ–Морса

0,1,1,0,1,0,0,1,1,0,0,1,0,1,1,0...

формируется новая последовательность, в которой каждый член представляет собой разность двух последовательных членов последовательности Туэ – Морса. Полученное слово без квадратов будет

1,0,-1,1,-1,0,1,0,-1,0,1,-1,1,0,-1,...

(последовательность A029883 в OEIS ).

Пиявки Морфизм

Еще один пример, найденный Джоном Личем. ^[10] определяется рекурсивно по алфавиту $\{0,1,2\}$ . Пусть ⁠ $w_{1}$ ⁠ — любое слово без квадратов, начинающееся с буквы 0 . Дайте определение словам $\{w_{i}\mid i\in \mathbb {N} \}$ рекурсивно следующим образом: слово $w_{i+1}$ получается из ⁠ $w_{i}$ ⁠ заменив каждый 0 в ⁠ $w_{i}$ ⁠ с 0121021201210 , каждый 1 с 1202102012021 и каждый 2 с 2010210120102 . Можно доказать, что последовательность сходится к бесконечному бесквадратному слову

0121021201210120210201202120102101201021202102012021...

Генерация бесконечных слов без квадратов

Бесконечные слова без квадратов могут быть сгенерированы с помощью морфизма без квадратов . Морфизм называется бесквадратным, если образ каждого бесквадратного слова является бесквадратным. Морфизм называется k-бесквадратным, если образ каждого бесквадратного слова длины k бесквадратный.

Крочемор ^[11] доказывает, что равномерный морфизм $h$ свободен от квадратов тогда и только тогда, когда он свободен от 3-квадратов. Другими словами, $h$ бесквадратен тогда и только тогда, когда $h(w)$ является бесквадратным для всех бесквадратных $w$ длины 3. Можно найти бесквадратный морфизм методом перебора .

algorithm square-free_morphism is
    output: a square-free morphism with the lowest possible rank  $k$ .

    set  $k=3$ 
    while True do
        set k_sf_words to the list of all square-free words of length  $k$  over a ternary alphabet
        for each  $h(0)$  in k_sf_words do
            for each  $h(1)$  in k_sf_words do
                for each  $h(2)$  in k_sf_words do
                    if  $h(1)=h(2)$  then
                        break from the current loop (advance to next  $h(1)$ )
                    if  $h(0)\neq h(1)$  and  $h(2)\neq h(0)$  then
                        if  $h(w)$  is square-free for all square-free  $w$  of length 3 then
                            return  $h(0),h(1),h(2)$ 
        increment  $k$  by 1

В троичном алфавите существует ровно 144 равномерных бесквадратных морфизма ранга 11 и нет равномерных бесквадратных морфизмов ранга ниже 11.

Чтобы получить бесконечные слова без квадратов, начните с любого слова без квадратов, такого как 0 , и последовательно примените к нему морфизм без квадратов $h$ . Полученные слова сохраняют свойство свободы от квадратов. Например, пусть $h$ — морфизм без квадратов, тогда как $w\to \infty$ , $h^{w}(0)$ — бесконечное слово без квадратов.

Заметим, что если морфизм над троичным алфавитом не является равномерным, то этот морфизм бесквадратен тогда и только тогда, когда он свободен от 5 квадратов. ^[11]

Сочетания букв в словах без квадратов

Расширение слова без квадратов, чтобы избежать $ab$ .

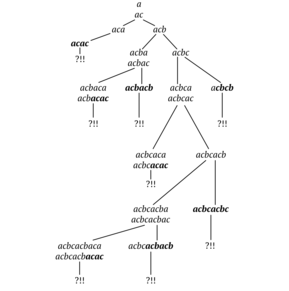
Избегайте двухбуквенных комбинаций

В троичном алфавите слово без квадратов длиной более 13 содержит все двухбуквенные комбинации без квадратов. ^[12]

Это можно доказать, построив слово без квадратов без двухбуквенного сочетания $ab$ . В результате $bcba$ $cbca$ $cbaca$ — самое длинное слово без квадратов без комбинации $ab$ и его длина равна 13.

Обратите внимание, что в алфавите, состоящем более чем из трех букв, существуют слова любой длины без квадратов без произвольной комбинации двух букв.

Избегайте трехбуквенных комбинаций

В троичном алфавите слово без квадратов длиной более 36 содержит все трехбуквенные комбинации без квадратов. ^[12]

Однако существуют слова любой длины без квадратов без трехбуквенного сочетания $аба$ .

Обратите внимание, что в алфавите, состоящем более чем из трех букв, существуют слова любой длины без квадратов без произвольной трехбуквенной комбинации.

Плотность буквы

Плотность буквы $а$ в конечном слове $w$ определяется как ${\frac {|w|_{a}}{|w|}}$ где $|w|_{a}$ количество вхождений $a$ в $w$ и $|w|$ это длина слова. Плотность буквы $а$ в бесконечном слове равна $\liminf _{l\to \infty }{\frac {|w_{l}|_{a}}{|w_{l}|}}$ где $w_{l}$ — префикс слова $w$ длины $l$ . ^[13]

Минимальная плотность буквы $а$ в бесконечном троичном слове без квадратов равна ${\frac {883}{3215}}\approx 0.2747$ . ^[13]

Максимальная плотность буквы $а$ в бесконечном троичном слове без квадратов равна ${\frac {255}{653}}\approx 0.3905$ . ^[14]

Примечания

^ «А006156 - ОЭИС» . oeis.org . Проверено 28 марта 2019 г.
^ Jump up to: ^а ^б ^с Шур, Арсений (2011). «Свойства роста бесстепенных языков». Обзор компьютерных наук . 6 (5–6): 28–43. дои : 10.1016/j.cosrev.2012.09.001 .
^ Берта, Валери; Риго, Мишель, ред. (2016), «Предисловие», Комбинаторика, слова и символическая динамика , Cambridge University Press, стр. xi – xviii, doi : 10.1017/cbo9781139924733.001 , ISBN 9781139924733
^ Карпи, Артуро (1988). «Многомерные неповторяющиеся конфигурации» . Теоретическая информатика . 56 (2): 233–241. дои : 10.1016/0304-3975(88)90080-1 . ISSN 0304-3975 .
^ Шур, Арсений (2015). «Эффективное создание слов без квадратов» . Теоретическая информатика . 601 : 67–72. дои : 10.1016/j.tcs.2015.07.027 . hdl : 10995/92700 .
^ Апостолико, А.; Препарата, ФП (февраль 1983 г.). «Оптимальное автономное обнаружение повторов в строке» . Теоретическая информатика . 22 (3): 297–315. дои : 10.1016/0304-3975(83)90109-3 . ISSN 0304-3975 .
^ Крочемор, Макс (октябрь 1981 г.). «Оптимальный алгоритм вычисления повторений в слове». Письма об обработке информации . 12 (5): 244–250. дои : 10.1016/0020-0190(81)90024-7 . ISSN 0020-0190 .
^ Мэйн, Майкл Дж; Лоренц, Ричард Дж (сентябрь 1984 г.). «Алгоритм O (n log n) для поиска всех повторений в строке». Журнал алгоритмов . 5 (3): 422–432. дои : 10.1016/0196-6774(84)90021-x . ISSN 0196-6774 .
^ Jump up to: ^а ^б Берстель, Жан (1994). Статьи Акселя Туэ о повторах в словах и переводе . Кафедры математики и информатики Квебекского университета в Монреале. ISBN 978-2892761405 . OCLC 494791187 .
^ Пиявка, Дж. (1957). «Задача о нитках бус». Математика. Газ . 41 : 277–278. дои : 10.1017/S0025557200236115 . S2CID 126406225 . Збл 0079.01101 .
^ Jump up to: ^а ^б Берстель, Жан (апрель 1984 г.). «Некоторые недавние результаты по словам без квадратов» . Ежегодный симпозиум по теоретическим аспектам информатики . Конспекты лекций по информатике. 166 : 14–25. дои : 10.1007/3-540-12920-0_2 . ISBN 978-3-540-12920-2 .
^ Jump up to: ^а ^б Золотов, Борис (2015). «Еще одно решение проблемы неповторяющихся слов». arXiv : 1505.00019 [ math.CO ].
^ Jump up to: ^а ^б Халявин, Андрей (2007). «Минимальная плотность буквы в бесконечном троичном слове без квадратов равна 883/3215» (PDF) . Журнал целочисленных последовательностей . 10 (2): 3. Бибкод : 2007JIntS..10...65K .
^ Охем, Паскаль (2007). «Частота букв в бесконечных словах без повторений». Теоретическая информатика . 380 (3): 388–392. дои : 10.1016/j.tcs.2007.03.027 . ISSN 0304-3975 .

Ссылки

Берстель, Жан ; Лауве, Аарон; Ройтенауэр, Кристоф; Салиола, Франко В. (2009). Комбинаторика слов. Слова Кристоффеля и повторы в словах . Серия монографий по CRM. Том. 27. Провиденс, Род-Айленд: Американское математическое общество . ISBN 978-0-8218-4480-9 . Коллекция 1161.68043 .
Лотер, М. (1997). Комбинаторика слов . Кембридж: Издательство Кембриджского университета . ISBN 978-0-521-59924-5 . .
Лотер, М. (2011). Алгебраическая комбинаторика на словах . Энциклопедия математики и ее приложений. Том. 90. С предисловием Жана Берстеля и Доминика Перрена (перепечатка издания 2002 г. в твердом переплете). Издательство Кембриджского университета . ISBN 978-0-521-18071-9 . Артикул 1221.68183 .
Пифей Фогг, Н. (2002). Берта, Валери ; Ференци, Себастьен; Модуит, Кристиан; Сигел, Энн (ред.). Замены в динамике, арифметике и комбинаторике . Конспект лекций по математике. Том. 1794. Берлин: Springer-Verlag . ISBN 978-3-540-44141-0 . Збл 1014.11015 .

[1] «А006156 - ОЭИС» . oeis.org . Проверено 28 марта 2019 г.

[:1-2] Jump up to: ^а ^б ^с Шур, Арсений (2011). «Свойства роста бесстепенных языков». Обзор компьютерных наук . 6 (5–6): 28–43. дои : 10.1016/j.cosrev.2012.09.001 .

[3] Берта, Валери; Риго, Мишель, ред. (2016), «Предисловие», Комбинаторика, слова и символическая динамика , Cambridge University Press, стр. xi – xviii, doi : 10.1017/cbo9781139924733.001 , ISBN 9781139924733

[4] Карпи, Артуро (1988). «Многомерные неповторяющиеся конфигурации» . Теоретическая информатика . 56 (2): 233–241. дои : 10.1016/0304-3975(88)90080-1 . ISSN 0304-3975 .

[5] Шур, Арсений (2015). «Эффективное создание слов без квадратов» . Теоретическая информатика . 601 : 67–72. дои : 10.1016/j.tcs.2015.07.027 . hdl : 10995/92700 .

[6] Апостолико, А.; Препарата, ФП (февраль 1983 г.). «Оптимальное автономное обнаружение повторов в строке» . Теоретическая информатика . 22 (3): 297–315. дои : 10.1016/0304-3975(83)90109-3 . ISSN 0304-3975 .

[7] Крочемор, Макс (октябрь 1981 г.). «Оптимальный алгоритм вычисления повторений в слове». Письма об обработке информации . 12 (5): 244–250. дои : 10.1016/0020-0190(81)90024-7 . ISSN 0020-0190 .

[8] Мэйн, Майкл Дж; Лоренц, Ричард Дж (сентябрь 1984 г.). «Алгоритм O (n log n) для поиска всех повторений в строке». Журнал алгоритмов . 5 (3): 422–432. дои : 10.1016/0196-6774(84)90021-x . ISSN 0196-6774 .

[:4-9] Jump up to: ^а ^б Берстель, Жан (1994). Статьи Акселя Туэ о повторах в словах и переводе . Кафедры математики и информатики Квебекского университета в Монреале. ISBN 978-2892761405 . OCLC 494791187 .

[10] Пиявка, Дж. (1957). «Задача о нитках бус». Математика. Газ . 41 : 277–278. дои : 10.1017/S0025557200236115 . S2CID 126406225 . Збл 0079.01101 .

[:0-11] Jump up to: ^а ^б Берстель, Жан (апрель 1984 г.). «Некоторые недавние результаты по словам без квадратов» . Ежегодный симпозиум по теоретическим аспектам информатики . Конспекты лекций по информатике. 166 : 14–25. дои : 10.1007/3-540-12920-0_2 . ISBN 978-3-540-12920-2 .

[:2-12] Jump up to: ^а ^б Золотов, Борис (2015). «Еще одно решение проблемы неповторяющихся слов». arXiv : 1505.00019 [ math.CO ].

[:3-13] Jump up to: ^а ^б Халявин, Андрей (2007). «Минимальная плотность буквы в бесконечном троичном слове без квадратов равна 883/3215» (PDF) . Журнал целочисленных последовательностей . 10 (2): 3. Бибкод : 2007JIntS..10...65K .

[14] Охем, Паскаль (2007). «Частота букв в бесконечных словах без повторений». Теоретическая информатика . 380 (3): 388–392. дои : 10.1016/j.tcs.2007.03.027 . ISSN 0304-3975 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]