Видообразование ионов

Видообразование ионов изменению концентрации различных форм иона при изменении pH раствора относится к .

Соотношение кислоты AH и сопряженного основания A ⁻ концентрации варьируются по мере изменения разницы между pH и p K _a в соответствии с уравнением Хендерсона-Хассельбаха .

pH раствора монопротонной слабой кислоты можно выразить через степень диссоциации. После перестановки выражения, определяющего константу диссоциации кислоты , и помещения pH = -log ₁₀ [H ⁺ ], получаем

pH = p K _a – log ( [AH]/[A ⁻ ] )

Это разновидность уравнения Хендерсона-Хассельбаха . Из этого выражения можно сделать вывод, что

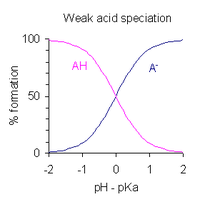
• когда кислота диссоциирована на 1 %, то есть когда [AH]/[A ⁻ ] = 100, pH = p K _a − 2
• когда кислота диссоциирована на 50 %, т. е. когда [AH]/[A ⁻ ] = 1, pH = p K _а
• когда кислота диссоциирована на 99 %, то есть когда [AH]/[A ⁻ ] = 0,01, pH = p K _a + 2

Отсюда следует, что диапазон pH, в котором происходит частичная диссоциация кислоты, составляет около p K _a ± 2. Это показано графически справа.

Практическое применение этих результатов состоит в том, что диапазон перехода pH индикатора pH составляет примерно p K _a ± 1; цвет индикатора в кислотной форме отличается от цвета сопряженной основной формы. В переходном диапазоне обе формы находятся в равновесии, поэтому цвет является промежуточным. За пределами переходного диапазона концентрация кислоты или сопряженного основания составляет менее 10 %, а цвет основных частиц доминирует.

Концентрации видов рассчитаны с помощью программы HySS для 10 мМ раствора лимонной кислоты . р К _а1 = 3,13, р К _а2 = 4,76, р К _а3 = 6,40.

может Слабая кислота быть определена как кислота с p K _a больше примерно -2. Кислота с p K _a = −2 будет диссоциировать на 99 % при pH 0, то есть в 1 М растворе HCl. Любая кислота с ap K _a меньше примерно -2 называется сильной кислотой . Говорят, что сильные кислоты полностью диссоциированы. Не существует точного pKa, _{значения} позволяющего различать сильные и слабые кислоты, поскольку сильные кислоты, такие как серная кислота , связаны в очень концентрированном растворе.

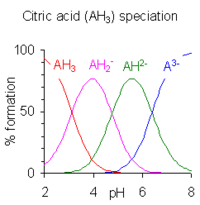
Расчет концентраций видов полипротонной кислоты более сложен, если значения p K не разделены на четыре или более, поскольку три или более видов могут сосуществовать при данном pH. Пример лимонной кислоты показан справа. Области pH, в которых существуют виды, сильно перекрываются, поскольку разница между последовательными значениями p K _a невелика. Опубликовано большое количество компьютерных программ для расчета равновесных концентраций веществ. Большинство из них могут поддерживать гораздо более сложные равновесия, чем кислотно-основные равновесия в растворе. Подробную информацию о программах общего назначения см. в компьютерных программах для расчета концентрации веществ в химическом равновесии .

См. также

• Бьеррумский сюжет
• Уравнение Шарло
• Уравнение Хендерсона – Хассельбаха