Проблема с решеткой

В информатике называемыми задачи решетки представляют собой класс задач оптимизации , связанных с математическими объектами, решетками . Предполагаемая неразрешимость таких проблем занимает центральное место в построении безопасных криптосистем на основе решетки : проблемы решетки являются примером NP-сложных задач, которые, как было показано, являются сложными в среднем случае , обеспечивая тестовый пример безопасности криптографических алгоритмов. Кроме того, некоторые решеточные задачи, которые являются трудными в наихудшем случае, могут быть использованы в качестве основы для чрезвычайно безопасных криптографических схем. Использование в таких схемах жесткости наихудшего случая делает их одними из очень немногих схем, которые с большой вероятностью защищены даже от квантовых компьютеров . Для приложений в таких криптосистемах решётки над векторными пространствами (часто $\mathbb {Q} ^{n}$) или бесплатные модули (часто $\mathbb {Z} ^{n}$) обычно считаются.

Для всех задач, приведенных ниже, предположим, что нам даны (в дополнение к другим более конкретным входным данным) базис векторного пространства V и норма N . Нормой обычно считается евклидова норма L ² . Однако другие нормы (например, L ^п ) также учитываются и отображаются в различных результатах.

На протяжении всей этой статьи пусть $\lambda (L)$ обозначаем длину кратчайшего ненулевого вектора в решетке L : то есть,

$\lambda (L)=\min _{v\in L\smallsetminus \{\mathbf {0} \}}\|v\|_{N}.$

Задача кратчайшего вектора (SVP)

Это иллюстрация задачи о кратчайшем векторе (базисные векторы показаны синим цветом, кратчайший вектор - красным).

В СВП базис векторного пространства V и норма N (часто L ² ) даны для решетки L , и необходимо найти кратчайший ненулевой вектор в V , измеренный N , в L . Другими словами, алгоритм должен вывести ненулевой вектор v такой, что ⁠ $\|v\|_{N}=\lambda (L)$⁠ .

В версии γ-аппроксимации SVP _γ необходимо найти ненулевой вектор решетки длины не более $\gamma \cdot \lambda (L)$ для данного ⁠ $\gamma \geq 1$⁠ .

Результаты твердости

Точная версия проблемы известна только как NP-трудная для рандомизированных сокращений. Напротив, соответствующая задача относительно равномерной нормы известна как NP-трудная .

Алгоритмы евклидовой нормы

Для решения точного варианта СВП по евклидовой норме известно несколько различных подходов, которые можно разделить на два класса: алгоритмы, требующие суперэкспоненциального времени ( $2^{\omega (n)}$) и $\operatorname {poly} (n)$ память и алгоритмы, требующие как экспоненциального времени, так и пространства ( $2^{\Theta (n)}$) в размерности решетки. Первый класс алгоритмов в первую очередь включает в себя решеточное перечисление. и сокращение случайной выборки, в то время как последний включает решетчатое сито, вычисление ячейки Вороного решетки, и дискретная гауссовая выборка. Открытой является проблема: существуют ли алгоритмы решения точных СВП, работающие за одно экспоненциальное время ( $2^{O(n)}$) и требующие полиномиального масштабирования памяти по размерности решетки.

Чтобы решить версию γ-аппроксимации SVP _γ для $\gamma >1$ для евклидовой нормы наиболее известные подходы основаны на использовании редукции решеточного базиса . Для больших ⁠ $\gamma =2^{\Omega (n)}$⁠ алгоритм Ленстры-Ленстры-Ловаса (LLL) может найти решение за полиномиальное время от размерности решетки. Для меньших значений $\gamma$, блочный алгоритм Коркина-Золотарева (БКЗ) обычно используется, когда входные данные для алгоритма (размер блока $\beta$) определяет временную сложность и качество вывода: для больших коэффициентов аппроксимации $\gamma$, небольшой размер блока $\beta$ достаточно, и алгоритм быстро завершает работу. Для маленьких $\gamma$, больше $\beta$ необходимы для нахождения достаточно коротких векторов решетки, и алгоритму требуется больше времени для поиска решения. Алгоритм BKZ внутренне использует точный алгоритм SVP в качестве подпрограммы (работающей в решетках размерностью не более $\beta$), и его общая сложность тесно связана со стоимостью вызовов SVP в измерении ⁠ $\beta$⁠ .

ГапСВП

Задача GapSVP _β состоит в различении экземпляров SVP, в которых длина кратчайшего вектора не превосходит $1$ или больше ⁠ $\beta$⁠ , где $\beta$ может быть фиксированной функцией размера решетки ⁠ $n$⁠ . Учитывая основу решетки, алгоритм должен решить, будет ли $\lambda (L)\leq 1$ или ⁠ $\lambda (L)>\beta$⁠ . Как и в других задачах с обещаниями , алгоритму разрешена ошибка во всех остальных случаях.

Еще один вариант проблемы — GapSVP _ζ,γ для некоторых функций ζ и γ. Входные данные для алгоритма являются основой $B$ и номер $d$. Гарантируется, что все векторы в ортогонализации Грама–Шмидта имеют длину не менее 1 и что $\lambda (L(B))\leq \zeta (n)$ и это ⁠ $1\leq d\leq \zeta (n)/\gamma (n)$⁠ , где $n$ это размерность. Алгоритм должен принять, если ⁠ $\lambda (L(B))\leq d$⁠ и отклонить, если ⁠ $\lambda (L(B))\geq \gamma (n)\cdot d$⁠ . Для больших $\zeta$ (т.е. ⁠ $\zeta (n)>2^{n/2}$⁠ ), проблема эквивалентна GapSVP _γ, поскольку предварительная обработка, выполненная с использованием алгоритма LLL, создает второе условие (и, следовательно, ⁠ $\zeta$⁠ ) ​​избыточно.

Задача ближайшего вектора (CVP)

Это иллюстрация задачи о ближайшем векторе (базисные векторы показаны синим, внешний вектор - зеленым, ближайший вектор - красным).

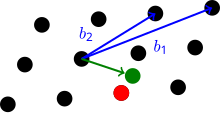
В CVP базис векторного пространства V и метрика M (часто L ² ) даны для решетки L , а также вектора v в V но не обязательно в L. , Требуется найти вектор в L, ближайший к v (измеренный M ). В $\gamma$-версия аппроксимации CVP _γ , необходимо найти вектор решетки на расстоянии не более $\gamma$.

Отношения со старшим вице-президентом

Задача о ближайшей векторной задаче является обобщением задачи о кратчайшей векторной задаче. Легко показать, что, имея оракул для CVP _γ (определенный ниже), можно решить SVP _γ, сделав несколько запросов к оракулу. Наивный метод поиска кратчайшего вектора путем вызова оракула CVP _γ для поиска вектора, ближайшего к 0, не работает, поскольку 0 сам по себе является вектором решетки, и алгоритм потенциально может вывести 0.

Сведение от SVP _γ к CVP _γ заключается в следующем: предположим, что входные данные для SVP _γ являются базой для решетки $B=[b_{1},b_{2},\ldots ,b_{n}]$. Рассмотрим основу $B^{i}=[b_{1},\ldots ,2b_{i},\ldots ,b_{n}]$ и пусть $x_{i}$ быть вектором, возвращаемым CVP _γ ( B ^я , б _я ) . Утверждается, что кратчайший вектор в множестве $\{x_{i}-b_{i}\}$ – кратчайший вектор в данной решетке.

Результаты твердости

Голдрейх и др. показали, что любая твердость СВП предполагает такую ​​же твердость и ЦВП. Используя инструменты PCP , Arora et al. показали, что CVP трудно аппроксимировать с точностью до коэффициента $2^{\log ^{1-\epsilon }(n)}$ пока не $\operatorname {NP} \subseteq \operatorname {DTIME} (2^{\operatorname {poly} (\log n)})$. Динур и др. усилил это, дав результат NP-твердости с $\epsilon =(\log \log n)^{c}$ для $c<1/2$.

Сферное декодирование

Алгоритмы CVP, особенно вариант Финке и Поста, использовались для обнаружения данных в системах беспроводной связи с несколькими входами и множеством выходов ( MIMO ) (для кодированных и некодированных сигналов). В этом контексте это называется сферным декодированием из-за внутреннего радиуса, используемого во многих решениях CVP.

Он был применен в области разрешения целочисленной неоднозначности GNSS с фазой несущей (GPS). это называется методом LAMBDA В этой области . В той же области общая задача CVP называется целочисленными наименьшими квадратами .

ГэпЦВП

Эта проблема аналогична проблеме GapSVP. Для GapSVP _β входные данные состоят из базиса решетки и вектора $v$, и алгоритм должен ответить, выполняется ли одно из следующих условий:

• существует вектор решетки такой, что расстояние между ним и $v$ не более 1, и
• каждый вектор решетки находится на расстоянии большем, чем $\beta$ вдали от $v$.

Противоположное условие состоит в том, что ближайший вектор решетки находится на расстоянии $1<\lambda (L)\leq \beta$отсюда и название Gap CVP.

Известные результаты

Задача тривиально содержится в NP для любого коэффициента аппроксимации.

Шнорр в 1987 году показал, что детерминированные алгоритмы с полиномиальным временем могут решить проблему для $\beta =2^{O(n(\log \log n)^{2}/\log n)}$. Айтай и др. показали, что вероятностные алгоритмы могут достичь немного лучшего коэффициента аппроксимации $\beta =2^{O(n\log \log n/\log n)}$.

В 1993 году Банащик показал, что GapCVP _n находится в ${\mathsf {NP\cap coNP}}$. В 2000 году Гольдрайх и Гольдвассер показали, что $\beta ={\sqrt {n/\log n}}$ ставит проблему как в NP, так и в coAM . В 2005 году Ааронов и Регев показали, что для некоторой постоянной $c$, проблема с $\beta =c{\sqrt {n}}$ находится в ${\mathsf {NP\cap coNP}}$.

Что касается нижних границ, Динур и др. показали в 1998 году, что задача NP-трудна для $\beta =n^{o(1/\log {\log {n}})}$.

Задача кратчайших независимых векторов (SIVP)

Учитывая решетку L размерности n , алгоритм должен вывести n линейно независимых $v_{1},v_{2},\ldots ,v_{n}$ так что $\max \|v_{i}\|\leq \max _{B}\|b_{i}\|$, где правая часть учитывает все базы $B=\{b_{1},\ldots ,b_{n}\}$ решетки.

В $\gamma$-приближенный вариант, учитывая решетку L размерности n , нужно найти n линейно независимых векторов $v_{1},v_{2},\ldots ,v_{n}$ длины ⁠ $\max \|v_{i}\|\leq \gamma \lambda _{n}(L)$⁠ , где $\lambda _{n}(L)$ это ⁠ $n$⁠ ^й последовательный минимум ⁠ $L$⁠ .

Декодирование ограниченного расстояния

Эта проблема аналогична CVP. Дан вектор такой, что его расстояние от решетки не более $\lambda (L)/2$, алгоритм должен вывести ближайший к нему вектор решетки.

Проблема с радиусом покрытия

Учитывая основу решетки, алгоритм должен найти наибольшее расстояние (или, в некоторых версиях, его аппроксимацию) от любого вектора до решетки.

Задача о кратчайшем базисе

Многие задачи становятся проще, если входной базис состоит из коротких векторов. Алгоритм, решающий задачу кратчайшего базиса (SBP), должен, учитывая решетчатый базис ⁠ $B$⁠ , выведите эквивалентный базис $B'$ такая, что длина самого длинного вектора в $B'$ является максимально коротким.

Задача аппроксимации SBP _γ состоит в поиске базиса, самый длинный вектор которого не превышает $\gamma$ раз длиннее, чем самый длинный вектор в самом коротком базисе.

Использование в криптографии

Основная статья: Решеточная криптография

Средняя сложность задач составляет основу доказательства безопасности большинства криптографических схем. Однако экспериментальные данные показывают, что большинство NP-сложных задач лишены этого свойства: они, вероятно, сложны только в худшем случае. Было высказано предположение или доказано, что многие задачи о решетках сложны в среднем случае, что делает их привлекательным классом задач для построения криптографических схем. Более того, сложность некоторых решеточных задач в наихудшем случае использовалась для создания безопасных криптографических схем. Использование в таких схемах жесткости наихудшего случая делает их одними из очень немногих схем, которые с большой вероятностью защищены даже от квантовых компьютеров .

Вышеупомянутые проблемы с решеткой легко решить, если алгоритм имеет «хорошую» основу. Алгоритмы сокращения решетки стремятся, учитывая основу решетки, вывести новый базис, состоящий из относительно коротких, почти ортогональных векторов. Алгоритм приведения решеточного базиса Ленстры-Ленстры-Ловаса (LLL) был первым эффективным алгоритмом для решения этой проблемы, который мог выводить почти уменьшенный решеточный базис за полиномиальное время. Этот алгоритм и его дальнейшие усовершенствования были использованы для взлома нескольких криптографических схем, что установило его статус очень важного инструмента криптоанализа. Успех LLL на экспериментальных данных привел к убеждению, что уменьшение решетки может оказаться легкой проблемой на практике; однако это убеждение было поставлено под сомнение в конце 1990-х годов, когда было получено несколько новых результатов о сложности решеточных задач, начиная с результата Айтая .

В своих основополагающих статьях Айтай показал, что проблема SVP является NP-трудной, и обнаружил некоторые связи между сложностью наихудшего случая и сложностью среднего случая некоторых решеточных задач. Опираясь на эти результаты, Айтай и Дворк создали криптосистему с открытым ключом , безопасность которой можно было доказать, используя только наихудшую сложность определенной версии SVP. таким образом, это первый результат, в котором для создания безопасных систем использовалась жесткость наихудшего случая.

См. также

• Обучение с ошибками
• Задача о коротком целочисленном решении

Дальнейшее чтение

• Агрелл, Э.; Эрикссон, Т.; Варди, А.; Зегер, К. (2002). «Поиск ближайшей точки в решетках» (PDF) . IEEE Транс. Инф. Теория . 48 (8): 2201–2214. дои : 10.1109/TIT.2002.800499 .
• Мичиансио, Даниэле (2001). «Задачу о кратчайшем векторе {NP} трудно аппроксимировать с точностью до некоторой константы» . SIAM Journal по вычислительной технике . 30 (6): 2008–2035. CiteSeerX   10.1.1.93.6646 . дои : 10.1137/S0097539700373039 . S2CID   42794945 .
• Нгуен, Фонг К.; Стерн, Жак (2000). «Сокращение решеток в криптологии: обновление» . Труды 4-го Международного симпозиума по алгоритмической теории чисел . Спрингер-Верлаг. стр. 85–112. ISBN  978-3-540-67695-9 .