Равнобедренный набор

Уникальный 6-точечный равнобедренный набор на плоскости. Заштрихованные области показывают четыре из 20 равнобедренных треугольников, образованных тройками этих точек.

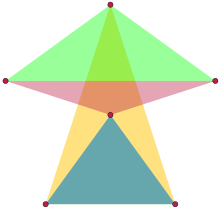
В дискретной геометрии называется равнобедренным множеством множество точек, каждая из которых образует равнобедренный треугольник . Точнее, каждые три точки должны определять не более двух расстояний; это также позволяет создавать вырожденные равнобедренные треугольники, образованные тремя точками, расположенными на равном расстоянии друг от друга на линии.

История

Проблема нахождения наибольшего равнобедренного множества в евклидовом пространстве заданной размерности была поставлена ​​в 1946 году Полом Эрдешем . В своей постановке задачи Эрдеш заметил, что самый большой такой набор в евклидовой плоскости имеет шесть точек. В своем решении 1947 года Лерой Милтон Келли еще убедительнее показал, что уникальное плоское равнобедренное множество из шести точек состоит из вершин и центра правильного пятиугольника . В трех измерениях Келли нашел равнобедренный набор из восьми точек, шесть точек из которых одинаковы; остальные две точки лежат на линии, перпендикулярной пятиугольнику, проходящей через его центр, на том же расстоянии, что и вершины пятиугольника от центра. Позже было доказано, что этот трехмерный пример является оптимальным и единственным оптимальным решением.

Разложение на множества двух расстояний

Трехмерное равнобедренное множество Келли из восьми точек можно разложить на два множества. $X$ (три точки на линии, перпендикулярной пятиугольнику) и $Y$ (пять вершин пятиугольника), со свойством, что каждая точка в $X$ равноудалена от всех точек $Y$. Когда такое разложение возможно в евклидовых пространствах любой размерности, $X$ и $Y$ должен лежать в перпендикулярных подпространствах, $X$ должно быть равнобедренным множеством внутри своего подпространства, а множество $Y'$ сформированный из $Y$ добавление точки на пересечении двух его подпространств также должно быть равнобедренным множеством внутри своего подпространства. Таким образом, равнобедренный набор в больших измерениях иногда можно разложить на равнобедренные наборы в меньших измерениях. С другой стороны, когда равнобедренное множество не имеет такого разложения, тогда оно должно обладать более сильным свойством, чем быть равнобедренным: оно имеет только два расстояния среди всех пар точек.

Несмотря на эту теорему о разложении, самый большой набор двух расстояний и самый большой равнобедренный набор в одном измерении могут иметь разные размеры. Это происходит, например, на плоскости, где наибольшее множество двух расстояний имеет пять точек (вершины правильного пятиугольника), а наибольшее равнобедренное множество имеет шесть точек. В этом случае шеститочечное равнобедренное множество имеет разложение, где $X$ - одноэлементное множество центральной точки (в пространстве нулевых измерений) и $Y$ состоит из всех остальных точек.

Верхние границы

В $d$-мерном пространстве равнобедренное множество может иметь не более $${\binom {d+2}{2}}$$точки. Это тесно для $d=6$ и для $d=8$ но не обязательно для других измерений.Максимальное количество баллов в $d$-мерное равнобедренное множество, для $d=1,2,\dots ,8$, как известно,

3, 6, 8, 11, 17, 28, 30, 45 (последовательность A175769 в OEIS )

но эти числа неизвестны для более высоких размерностей.

Строительство

Лисонек предлагает следующую конструкцию множеств двух расстояний с $${\binom {d+1}{2}}$$точек, что также создает равнобедренные множества с $${\binom {d+1}{2}}+1$$точки. В $d+1$-мерное евклидово пространство, пусть $e_{i}$ (для $i=1,\dots ,d+1$) обозначают вектор на единичном расстоянии от начала координат вдоль $i$ось координат и построим множество $S$ состоящий из всех точек $e_{i}+e_{j}$ для $i\neq j$. Затем $S$ лежит в $d$-мерное подпространство точек с суммой координат $2$; его выпуклая оболочка является гиперсимплексом $\Delta _{d+1,2}$. У него всего два расстояния: две точки, образованные из сумм перекрывающихся пар единичных векторов, имеют расстояние ${\sqrt {2}}$, а две точки, образованные из непересекающихся пар единичных векторов, имеют расстояние $2$. Добавляю еще один пункт $S$ в его центроиде образует $d$-мерное равнобедренное множество. Например, для $d=3$, эта конструкция создает субоптимальный равнобедренный набор с семью точками, вершинами и центром правильного октаэдра , а не оптимальный набор из восьми точек.

Обобщение

Эту же проблему можно рассмотреть и для других метрических пространств . Например, для пространств Хэмминга известны несколько меньшие верхние оценки, чем для евклидовых пространств той же размерности. В ультраметрическом пространстве все пространство (и любое его подмножество) представляет собой равнобедренное множество. Поэтому ультраметрические пространства иногда называют равнобедренными. Однако не каждое равнобедренное множество является ультраметрическим; например, тупоугольные равнобедренные евклидовы треугольники не являются ультраметрическими.