Дискретное преобразование Хартли

Дискретное преобразование Хартли (DHT) — это преобразование Фурье дискретных периодических данных, подобное дискретному преобразованию Фурье (DFT), с аналогичными приложениями в обработке сигналов и смежных областях. Его главное отличие от ДПФ состоит в том, что он преобразует реальные входные данные в реальные выходные данные без внутреннего участия комплексных чисел . Так же, как ДПФ является дискретным аналогом непрерывного преобразования Фурье (ПФ), ДНТ является дискретным аналогом непрерывного преобразования Хартли (НТ), введенного Ральфом В.Л. Хартли в 1942 году. ^[1]

Поскольку существуют быстрые алгоритмы для DHT, аналогичные быстрому преобразованию Фурье (FFT), DHT был первоначально предложен Рональдом Н. Брейсвеллом в 1983 году. ^[2] как более эффективный вычислительный инструмент в общем случае, когда данные являются чисто реальными. Однако впоследствии утверждалось, что специализированные алгоритмы БПФ для реальных входных или выходных данных обычно можно найти с помощью немного меньшего количества операций, чем любой соответствующий алгоритм для DHT.

Определение

Формально дискретное преобразование Хартли представляет собой линейную обратимую функцию H : R ^н → Р ^н (где R обозначает множество действительных чисел ). N , действительных чисел x ₀ , ..., x _{N −1} преобразуются в N действительных чисел H ₀ ..., H _{N −1} по формуле

H_{k}=\sum _{n=0}^{N-1}x_{n}\operatorname {cas} \left({\frac {2\pi }{N}}nk\right)=\sum _{n=0}^{N-1}x_{n}\left[\cos \left({\frac {2\pi }{N}}nk\right)+\sin \left({\frac {2\pi }{N}}nk\right)\right]\quad \quad k=0,\dots ,N-1.

Комбинация $\cos(z)+\sin(z)$ $={\sqrt {2}}\cos \left(z-{\frac {\pi }{4}}\right)$ иногда обозначается $cas(z)$ , и его не следует путать с $cis(z) = e iz = cos(z) + я sin(z)$ или $e - iz = cis(- z)$ , который появляется в определении ДПФ (где i — мнимая единица ).

Как и в случае с ДПФ, общий масштабный коэффициент перед преобразованием и знак синусоидального члена являются предметом соглашения. Хотя эти соглашения иногда различаются у разных авторов, они не влияют на основные свойства преобразования.

Характеристики

Преобразование можно интерпретировать как умножение вектора ( x ₀ , ...., x _{N -1} ) на N размера на N матрицу ; следовательно, дискретное преобразование Хартли является линейным оператором . Матрица обратима; обратное преобразование, которое позволяет восстановить x _n из H _k , представляет собой просто DHT H _{k ,} умноженное на 1/ N . То есть DHT является собственным обратным ( инволютивным ) с точностью до общего масштабного коэффициента.

DHT можно использовать для вычисления DFT и наоборот. Для реальных входных данных x _n выходной сигнал ДПФ X _k имеет действительную часть ( H _k + H _N−k )/2 и мнимую часть ( H _N−k − H _k )/2. И наоборот, DHT эквивалентно вычислению ДПФ x _n, умноженного на 1 + i , с последующим взятием действительной части результата.

Как и в случае с ДПФ, циклическая свертка z = x ∗ y двух векторов x = ( x _n ) и y = ( y _n ) для создания вектора z = ( z _n ), вся длина N , становится простой операцией после ДХТ. В частности, предположим, что векторы X , Y и Z обозначают DHT x , y и z соответственно. Тогда элементы Z задаются формулой:

{\begin{matrix}Z_{k}&=&\left[X_{k}\left(Y_{k}+Y_{N-k}\right)+X_{N-k}\left(Y_{k}-Y_{N-k}\right)\right]/2\\Z_{N-k}&=&\left[X_{N-k}\left(Y_{k}+Y_{N-k}\right)-X_{k}\left(Y_{k}-Y_{N-k}\right)\right]/2\end{matrix}}

где мы считаем все векторы периодическими по N ( X _N = X ₀ и так далее). Таким образом, так же, как ДПФ преобразует свертку в поточечное умножение комплексных чисел ( пар действительных и мнимых частей), ДГТ преобразует свертку в простую комбинацию пар вещественных частотных составляющих. Обратный DHT затем дает желаемый вектор z . Таким образом, быстрый алгоритм DHT (см. ниже) дает быстрый алгоритм свертки. (Это немного дороже, чем соответствующая процедура для ДПФ, не считая затрат на приведенные ниже преобразования, поскольку для парной операции, описанной выше, требуется 8 операций вещественной арифметики по сравнению с 6 операциями комплексного умножения. В этот подсчет не входит деление на 2, которое может быть включено, например, в нормализацию 1/ N обратного DHT.)

Быстрые алгоритмы

Как и в случае с ДПФ, непосредственная оценка определения ДНТ потребует O( N ²) арифметические операции (см. обозначение Big O ). Однако существуют быстрые алгоритмы, подобные БПФ, которые вычисляют тот же результат всего за O( N log N ) операций. Почти все алгоритмы БПФ, от Кули – Тьюки до простых коэффициентов и Винограда (1985). ^[3] Брууну ( 1993 ), ^[4] имеет прямой аналог дискретного преобразования Хартли. (Однако некоторые из наиболее экзотических алгоритмов БПФ, таких как QFT, еще не исследовались в контексте DHT.)

В частности, DHT-аналог алгоритма Кули-Тьюки широко известен как алгоритм быстрого преобразования Хартли (FHT) и был впервые описан Брейсвеллом в 1984 году. ^[5] Этот алгоритм FHT, по крайней мере, когда он применяется к степени двойки размерам N США , является предметом патента № 4,646,256, выданного в 1987 году Стэнфордскому университету . Стэнфорд разместил этот патент в открытом доступе в 1994 году (Bracewell, 1995). ^[6]

Как упоминалось выше, алгоритмы DHT обычно немного менее эффективны (с точки зрения количества операций с плавающей запятой ), чем соответствующий алгоритм DFT (FFT), специализирующийся на реальных входных (или выходных) данных. Впервые об этом заявили Соренсен и др. (1987) ^[7] и Дюамель и Веттерли (1987). ^[8] Последние авторы получили, по-видимому, наименьшее опубликованное количество операций для DHT размеров степени двойки, используя алгоритм разделения системы счисления (аналогичный БПФ с разделением системы счисления ), который разбивает DHT длины N на DHT длины N. длиной N /2 и два ДПФ реального ввода ( не DHT) длиной N /4. Таким образом, они утверждали, что ДХТ длины степени двойки можно вычислить, в лучшем случае, с помощью еще двух сложений, чем соответствующее количество арифметических операций для ДПФ с реальным входом.

На современных компьютерах производительность определяется больше соображениями кэша и конвейера ЦП , чем строгим подсчетом операций, и небольшая разница в арифметических затратах вряд ли будет существенной. Поскольку алгоритмы БПФ и БПФ с реальным входом имеют схожие вычислительные структуры, ни один из них, похоже, не имеет существенного априорного преимущества в скорости ( Попович [ ср ] и Шевич, 1994). ^[9] На практике высокооптимизированные библиотеки БПФ реального ввода доступны из многих источников (например, от поставщиков процессоров, таких как Intel ), тогда как высокооптимизированные библиотеки DHT встречаются реже.

С другой стороны, избыточные вычисления в БПФ из-за реальных входных данных труднее устранить для больших простых N , несмотря на существование алгоритмов комплексных данных O( N log N ) для таких случаев, поскольку избыточность скрыта за сложными перестановками. и/или чередование фаз в этих алгоритмах. Напротив, стандартный алгоритм БПФ простого размера, алгоритм Рейдера , может быть непосредственно применен к DHT реальных данных, требуя примерно в два раза меньше вычислений, чем эквивалентное комплексное БПФ (Frigo and Johnson, 2005). ^[10] С другой стороны, также возможна адаптация алгоритма Рейдера для ДПФ реального ввода, не основанная на DHT (Chu & Burrus , 1982). ^[11]

Многомерное дискретное преобразование Хартли (MD-DHT)

rD-DHT (MD-DHT с размерами «r») определяется выражением

$X(k_{1},k_{2},...,k_{r})=\sum _{n_{1}=0}^{N_{1}-1}\sum _{n_{2}=0}^{N_{2}-1}\dots \sum _{n_{r}=0}^{N_{r}-1}x(n_{1},n_{2},...,n_{r}){\rm {cas}}({\frac {2\pi n_{1}k_{1}}{N_{1}}}+\dots +{\frac {2\pi n_{r}k_{r}}{N_{r}}}),$

с $k_{i}=0,1,\ldots ,N_{i}-1$ и где ${\rm {cas}}(x)=\cos(x)+\sin(x).$

Как и в случае с 1D, MD-DHT как действительное и симметричное преобразование проще, чем MD-DFT. Во-первых, обратное DHT идентично прямому преобразованию, но с добавлением коэффициента масштабирования;

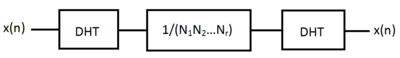
и во-вторых, поскольку ядро реально, оно позволяет избежать вычислительной сложности комплексных чисел . Кроме того, ДПФ можно получить непосредственно из ДГТ с помощью простой аддитивной операции (Брэйсвелл, 1983). ^[2]

MD-DHT широко используется в таких областях, как обработка изображений и оптических сигналов. Конкретные приложения включают компьютерное зрение, телевидение высокой четкости и телеконференции — области обработки или анализа движущихся изображений (Zeng, 2000). ^[12]

Быстрые алгоритмы для MD-DHT

Поскольку скорость вычислений продолжает расти, более крупные многомерные задачи становятся вычислительно осуществимыми, что требует необходимости в быстрых многомерных алгоритмах. Далее следуют три таких алгоритма.

В поисках разделимости для повышения эффективности мы рассмотрим следующее преобразование (Bracewell, 1983): ^[2]

${\hat {X}}(k_{1},k_{2},...,k_{r})=\sum _{n_{1}=0}^{N_{1}-1}\sum _{n_{2}=0}^{N_{2}-1}\dots \sum _{n_{r}=0}^{N_{r}-1}x(n_{1},n_{2},...,n_{r}){\rm {cas}}({\frac {2\pi n_{1}k_{1}}{N_{1}}})\dots {\rm {cas}}({\frac {2\pi n_{r}k_{r}}{N_{r}}}).$

Это было показано в Бортфельде (1995). ^[13] что эти два понятия могут быть связаны несколькими дополнениями. Например, в 3D,

$X(k_{1},k_{2},k_{3})={\frac {1}{2}}[{\hat {X}}(k_{1},k_{2},-k_{3})+{\hat {X}}(k_{1},-k_{2},k_{3})+{\hat {X}}(-k_{1},k_{2},k_{3})-{\hat {X}}(-k_{1},-k_{2},-k_{3})].$

Для ${\hat {X}}$ затем можно реализовать алгоритмы строк и столбцов. Этот метод обычно используется из-за простоты таких алгоритмов RC, но они не оптимизированы для общих пространств MD.

Были разработаны и другие быстрые алгоритмы, такие как основание счисления-2, основание счисления-4 и разделенное основание счисления. Например, Буссакта (2000). ^[14] разработал трехмерную векторную систему счисления,

$X(k_{1},k_{2},...,k_{r})=\sum _{n_{1}=0}^{N-1}\sum _{n_{2}=0}^{N-1}\sum _{n_{r}=0}^{N-1}x(n_{1},n_{2},n_{3}){\rm {cas}}({\frac {2\pi }{N}}(n_{1}k_{1}+n_{2}k_{2}+n_{3}k_{3}))$

$=\sum _{n_{1}:even}\sum _{n_{2}:even}\sum _{n_{3}:even}+\sum _{n_{1}:even}\sum _{n_{2}:even}\sum _{n_{3}:odd}+\sum _{n_{1}:even}\sum _{n_{2}:odd}\sum _{n_{3}:even}$

$+\sum _{n_{1}:even}\sum _{n_{2}:odd}\sum _{n_{3}:odd}+\sum _{n_{1}:odd}\sum _{n_{2}:even}\sum _{n_{3}:even}+\sum _{n_{1}:odd}\sum _{n_{2}:even}\sum _{n_{3}:odd}$

$+\sum _{n_{1}:odd}\sum _{n_{2}:odd}\sum _{n_{3}:even}+\sum _{n_{1}:odd}\sum _{n_{2}:odd}\sum _{n_{3}:odd}.$

Он также был представлен в Буссакте (2000). ^[14] что этот алгоритм счисления трехмерного вектора принимает $({\frac {7}{4}})N^{3}\log _{2}N$ умножения и $({\frac {31}{8}})N^{3}\log _{2}N$ дополнения по сравнению с $3N^{3}\log _{2}N$ умножения и $({\frac {9}{2}})N^{3}\log _{2}N+3N^{2}$ дополнения из подхода «строка-столбец». Недостаток заключается в том, что реализацию этих алгоритмов поразрядного типа трудно обобщить для сигналов произвольных размерностей.

Теоретико-числовые преобразования также использовались для решения MD-DHT, поскольку они выполняют чрезвычайно быстрые свертки. В Буссакте (1988 г.) ^[15] было показано, как разложить преобразование MD-DHT в форму, состоящую из сверток:

Для 2-D случая (3-D случай также описан в указанной ссылке)

$X(k,l)=\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}x(n,m){\rm {cas}}({\frac {2\pi nk}{N}}+{\frac {2\pi ml}{M}}),\;$ $k=0,1,\ldots ,N-1$ , $l=0,1,\ldots ,M-1$

можно разложить на одномерные и двумерные круговые свертки следующим образом:

$X(k,l)={\begin{cases}X_{1}(k,0)\\X_{2}(0,l)\\X_{3}(k,l)\end{cases}}$

где

$X_{1}(k,0)=\sum _{n=0}^{N-1}(\sum _{m=0}^{M-1}x(n,m)){\rm {cas}}({\frac {2\pi nk}{N}}),\;$ $k=0,1,\ldots ,N-1$

$X_{2}(0,l)=\sum _{m=0}^{M-1}(\sum _{n=0}^{N-1}x(n,m)){\rm {cas}}({\frac {2\pi ml}{M}}),\;$ $l=1,2,\dots ,M-1$

$X_{3}(k,l)=\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}x(n,m){\rm {cas}}({\frac {2\pi nk}{N}}+{\frac {2\pi ml}{M}})\;,$

$k=1,2,\ldots ,N-1$

$l=1,2,\ldots ,M-1.$

Разработка $X_{3}$ дальше,

$X_{3}(k,l)=\sum _{n=0}^{N-1}x(n,0){\rm {cas}}({\frac {2\pi nk}{N}})+\sum _{m=1}^{M-1}x(0,m){\rm {cas}}({\frac {2\pi ml}{M}})$

$+\sum _{n=1}^{N-1}\sum _{m=1}^{M-1}x(n,m){\rm {cas}}({\frac {2\pi nk}{N}}+{\frac {2\pi ml}{M}}).$

На этом этапе мы представляем преобразование числа Ферма (FNT). т ^й Число Ферма определяется выражением $F_{t}=2^{b}+1$ , с $b=2^{t}$ . Известные числа Ферма относятся к $t=0,1,2,3,4,5,6$ ( $F_{t}$ является лучшим для $0\leq t\leq 4$ ), (Буссакта, 1988). ^[15] Преобразование числа Ферма определяется выражением

$X(k,l)=\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}x(n,m)\alpha _{1}^{nk}\alpha _{2}^{ml}\mod F_{t}$

с $k=0,\ldots ,N-1,l=0,\ldots ,M-1$ . $\alpha _{1}$ и $\alpha _{2}$ являются корнями единства порядка $N$ и $M$ соответственно $(\alpha _{1}^{N}=\alpha _{2}^{M}=1\mod F_{t})$ .

Возвращаясь к разложению, последний член для $X_{3}(k,l)$ будет обозначаться как $X_{4}(k,l)$ , затем

$X_{4}(k,l)=\sum _{n=1}^{N-1}\sum _{m=1}^{M-1}x(n,m){\rm {cas}}({\frac {2\pi nk}{N}}+{\frac {2\pi ml}{M}}),$

$k=1,2,\ldots ,N-1$

$l=1,2,\ldots ,M-1.$

Если $g_{1}$ и $g_{2}$ являются примитивными корнями $N$ и $M$ (которые гарантированно существуют, если $M$ и $N$ простые ) , то $g_{1}$ и $g_{2}$ карта $(n,m)$ к $(g_{1}^{n}\mod N,g_{2}^{m}\mod M).$ Итак, картографирование $n,m,k$ и $l$ к $g_{1}^{-n},g_{2}^{-m},g_{1}^{k}$ и $g_{2}^{l}$ , получается следующее:

$X_{4}(g_{1}^{k},g_{2}^{l})=\sum _{n=0}^{N-2}\sum _{m=0}^{M-2}x(g_{1}^{-n},g_{2}^{-m}){\rm {cas}}({\frac {2\pi g_{1}^{(-n+k)}}{N}}+{\frac {2\pi g_{2}^{(-m+l)}}{M}}),$

$k=0,1,\ldots ,N-2$

$l=0,1,\ldots ,M-2$ .

Теперь это круговая свертка . С $Y(k,l)=X_{4}(g_{1}^{k},g_{2}^{l})$ , $y(n,m)=x(g_{1}^{-n},g_{2}^{-m})$ , и $h(n,m)={\rm {cas}}({\frac {2\pi g_{1}^{n}}{N}}+{\frac {2\pi g_{2}^{m}}{M}})$ , у одного есть

$Y(k,l)=\sum _{n=0}^{N-2}\sum _{m=0}^{M-2}y(n,m)h(<k-n>_{N},<l-m>_{M})$

$Y(k,l)=FNT^{-1}\{FNT[y(n,m)]\otimes FNT[h(n,m)]$

где $\otimes$ обозначает почленное умножение. Об этом также говорилось в (Boussakta, 1988). ^[15] что этот алгоритм уменьшает количество умножений в 8–20 раз по сравнению с другими алгоритмами DHT за счет небольшого увеличения количества операций сдвига и сложения, которые считаются более простыми, чем умножения. Недостаток этого алгоритма заключается в том, что каждое измерение преобразования имеет примитивный корень .

Ссылки

^ Хартли, Ральф В.Л. (март 1942 г.). «Более симметричный анализ Фурье применительно к задачам передачи». Труды ИРЭ . 30 (3): 144–150. дои : 10.1109/JRPROC.1942.234333 . S2CID 51644127 .
^ Jump up to: ^а ^б ^с Брейсвелл, Рональд Н. (1983). «Дискретное преобразование Хартли». Журнал Оптического общества Америки . 73 (12): 1832–1835. дои : 10.1364/josa.73.001832 . S2CID 120611904 .
^ Соренсен, Хенрик В.; Джонс, Дуглас Л .; Буррус, Чарльз Сидни ; Хайдеман, Майкл Т. (1985). «О вычислении дискретного преобразования Хартли». Транзакции IEEE по акустике, речи и обработке сигналов . АССП-33 (4): 1231–1238.
^ Бини, Дарио Андреа; Боззо, Энрико (1993). «Быстрое дискретное преобразование с помощью собственных многочленов» . Компьютеры и математика с приложениями . 26 (9): 35–52. дои : 10.1016/0898-1221(93)90004-ф .
^ Брейсвелл, Рональд Н. (1984). «Быстрое преобразование Хартли». Труды IEEE . 72 (8): 1010–1018. дои : 10.1109/proc.1984.12968 . S2CID 21988816 .
^ Брейсвелл, Рональд Н. (1995). «Вычисления с преобразованием Хартли» . Компьютеры в физике . 9 (4): 373–379. Бибкод : 1995ComPh...9..373B . дои : 10.1063/1.168534 .
^ Соренсен, Хенрик В.; Джонс, Дуглас Л .; Хайдеман, Майкл Т.; Буррус, Чарльз Сидни (1987). «Алгоритмы быстрого преобразования Фурье с действительными значениями». Транзакции IEEE по акустике, речи и обработке сигналов . ASSP-35 (6): 849–863.
^ Дюамель, Пьер; Веттерли, Мартин (1987). «Улучшенные алгоритмы преобразования Фурье и Хартли: применение к циклической свертке реальных данных». Транзакции IEEE по акустике, речи и обработке сигналов . АССП-35: 818–824.
^ Поповић [Попович], Миодраг [Миодраг] [на сербском] ; Шевич, Драгутин (1994). «Новый взгляд на сравнение быстрых преобразований Хартли и Фурье». Транзакции IEEE по обработке сигналов . 42 (8): 2178–2182. Бибкод : 1994ITSP...42.2178P . дои : 10.1109/78.301854 .
^ Фриго, Маттео; Джонсон, Стивен Г. (2005). «Проектирование и реализация FFTW3» (PDF) . Труды IEEE . 93 (2): 216–231. CiteSeerX 10.1.1.66.3097 . дои : 10.1109/jproc.2004.840301 . S2CID 6644892 . }
^ Чу, Шуни; Буррус, Чарльз Сидни (1982). «Алгоритм FTT с простым коэффициентом [ sic ] с использованием распределенной арифметики». Транзакции IEEE по акустике, речи и обработке сигналов . 30 (2): 217–227. дои : 10.1109/tassp.1982.1163875 .
^ Цзэн, Юнхан; Би, Гоань; Лейман, Абдул Рахим (2000). «Алгоритмы полиномиального преобразования для многомерного дискретного преобразования Хартли». Международный симпозиум IEEE по схемам и системам (V): 517–520.
^ Бортфельд, Томас; Динтер, Вольфганг (1995). «Расчет многомерных преобразований Хартли с использованием одномерных преобразований Фурье». Транзакции IEEE по обработке сигналов . 43 (5): 1306–1310. Бибкод : 1995ITSP...43.1306B . дои : 10.1109/78.382424 .
^ Jump up to: ^а ^б Буссакта, Саид; Альшибами, Усама (2000). «Быстрый алгоритм трехмерного дискретного преобразования Хартли». Международная конференция по акустике, речи и обработке сигналов '00 (4): 2302–2305.
^ Jump up to: ^а ^б ^с Буссакта, Саид; Холт, Алан Дж.Дж. (1988). «Быстрое многомерное дискретное преобразование Хартли с использованием преобразования числа Ферма». Слушания IEE G - Электронные схемы и системы . 135 (6): 235–237. дои : 10.1049/ip-g-1.1988.0036 .

Дальнейшее чтение

Брейсвелл, Рональд Н. (1986). Преобразование Хартли (1-е изд.). Издательство Оксфордского университета . ISBN 978-0-19503969-6 .
Буссакта, Саид; Холт, Алан Дж.Дж. (1988). «Быстрое многомерное дискретное преобразование Хартли с использованием преобразования числа Ферма». Слушания IEE G - Электронные схемы и системы . 135 (6): 235–237. дои : 10.1049/ip-g-1.1988.0036 .
Хонг, Джонатан; Веттерли, Мартин ; Дюамель, Пьер (1994). «Преобразование базового поля со свойством свертки» (PDF) . Труды IEEE . 82 (3): 400–412. дои : 10.1109/5.272145 .
О'Нил, Марк А. (1988). «Быстрее, чем быстрый Фурье». БАЙТ . 13 (4): 293–300.
Олнейничак, Крейг Дж.; Хейдт, Джеральд Т. (март 1994 г.). «Сканирование специального раздела преобразования Хартли». Труды IEEE . 82 : 372–380. (Примечание. Содержит обширную библиографию.)

[Hartley_1942-1] Хартли, Ральф В.Л. (март 1942 г.). «Более симметричный анализ Фурье применительно к задачам передачи». Труды ИРЭ . 30 (3): 144–150. дои : 10.1109/JRPROC.1942.234333 . S2CID 51644127 .

[Bracewell_1983-2] Jump up to: ^а ^б ^с Брейсвелл, Рональд Н. (1983). «Дискретное преобразование Хартли». Журнал Оптического общества Америки . 73 (12): 1832–1835. дои : 10.1364/josa.73.001832 . S2CID 120611904 .

[Sorensen_1985-3] Соренсен, Хенрик В.; Джонс, Дуглас Л .; Буррус, Чарльз Сидни ; Хайдеман, Майкл Т. (1985). «О вычислении дискретного преобразования Хартли». Транзакции IEEE по акустике, речи и обработке сигналов . АССП-33 (4): 1231–1238.

[Bini-Bozzo_1993-4] Бини, Дарио Андреа; Боззо, Энрико (1993). «Быстрое дискретное преобразование с помощью собственных многочленов» . Компьютеры и математика с приложениями . 26 (9): 35–52. дои : 10.1016/0898-1221(93)90004-ф .

[Bracewell_1984-5] Брейсвелл, Рональд Н. (1984). «Быстрое преобразование Хартли». Труды IEEE . 72 (8): 1010–1018. дои : 10.1109/proc.1984.12968 . S2CID 21988816 .

[Bracewell_1995-6] Брейсвелл, Рональд Н. (1995). «Вычисления с преобразованием Хартли» . Компьютеры в физике . 9 (4): 373–379. Бибкод : 1995ComPh...9..373B . дои : 10.1063/1.168534 .

[Sorensen_1987-7] Соренсен, Хенрик В.; Джонс, Дуглас Л .; Хайдеман, Майкл Т.; Буррус, Чарльз Сидни (1987). «Алгоритмы быстрого преобразования Фурье с действительными значениями». Транзакции IEEE по акустике, речи и обработке сигналов . ASSP-35 (6): 849–863.

[Duhamel-Vetterli_1987-8] Дюамель, Пьер; Веттерли, Мартин (1987). «Улучшенные алгоритмы преобразования Фурье и Хартли: применение к циклической свертке реальных данных». Транзакции IEEE по акустике, речи и обработке сигналов . АССП-35: 818–824.

[Popović-Šević_1994-9] Поповић [Попович], Миодраг [Миодраг] [на сербском] ; Шевич, Драгутин (1994). «Новый взгляд на сравнение быстрых преобразований Хартли и Фурье». Транзакции IEEE по обработке сигналов . 42 (8): 2178–2182. Бибкод : 1994ITSP...42.2178P . дои : 10.1109/78.301854 .

[Frigo-Johnson_2005-10] Фриго, Маттео; Джонсон, Стивен Г. (2005). «Проектирование и реализация FFTW3» (PDF) . Труды IEEE . 93 (2): 216–231. CiteSeerX 10.1.1.66.3097 . дои : 10.1109/jproc.2004.840301 . S2CID 6644892 . }

[Chu-Burrus_1982-11] Чу, Шуни; Буррус, Чарльз Сидни (1982). «Алгоритм FTT с простым коэффициентом [ sic ] с использованием распределенной арифметики». Транзакции IEEE по акустике, речи и обработке сигналов . 30 (2): 217–227. дои : 10.1109/tassp.1982.1163875 .

[Zeng-Bi-Leyman_2000-12] Цзэн, Юнхан; Би, Гоань; Лейман, Абдул Рахим (2000). «Алгоритмы полиномиального преобразования для многомерного дискретного преобразования Хартли». Международный симпозиум IEEE по схемам и системам (V): 517–520.

[Bortfeld-Dinter_1995-13] Бортфельд, Томас; Динтер, Вольфганг (1995). «Расчет многомерных преобразований Хартли с использованием одномерных преобразований Фурье». Транзакции IEEE по обработке сигналов . 43 (5): 1306–1310. Бибкод : 1995ITSP...43.1306B . дои : 10.1109/78.382424 .

[Boussakta_2000-14] Jump up to: ^а ^б Буссакта, Саид; Альшибами, Усама (2000). «Быстрый алгоритм трехмерного дискретного преобразования Хартли». Международная конференция по акустике, речи и обработке сигналов '00 (4): 2302–2305.

[Boussakta_1988-15] Jump up to: ^а ^б ^с Буссакта, Саид; Холт, Алан Дж.Дж. (1988). «Быстрое многомерное дискретное преобразование Хартли с использованием преобразования числа Ферма». Слушания IEE G - Электронные схемы и системы . 135 (6): 235–237. дои : 10.1049/ip-g-1.1988.0036 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]