График F26A
| График F26A | |
|---|---|
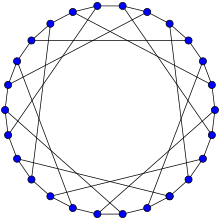 График F26A является гамильтоновым. | |
| Вершины | 26 |
| Края | 39 |
| Радиус | 5 |
| Диаметр | 5 |
| Обхват | 6 |
| Автоморфизмы | 78 (C13⋊C6) |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Характеристики | Граф Кэли Симметричный Кубический гамильтониан [1] |
| Таблица графиков и параметров | |
В математической области теории графов граф F26A представляет собой симметричный двудольный кубический граф с 26 вершинами и 39 ребрами. [1]
Он имеет хроматическое число 2, хроматический индекс 3, диаметр 5, радиус 5 и обхват 6. [2] Это также 3- вершинно-связный и 3- реберно-связный граф.
Граф F26A является гамильтоновым и может быть описан нотацией LCF [−7, 7] 13 .
Алгебраические свойства
[ редактировать ]Группа автоморфизмов графа F26A — это группа порядка 78. [3] Он действует транзитивно на вершинах, ребрах и дугах графа. Следовательно, граф F26A является симметричным графом (хотя и не транзитивным по расстоянию ). Он имеет автоморфизмы, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. Согласно переписи Фостера , граф F26A — единственный кубически-симметричный граф на 26 вершинах. [2] Это также граф Кэли для группы диэдра D 26 , порожденной a , ab и ab 4 , где: [4]
Граф F26A — это наименьший кубический граф, в котором группа автоморфизмов регулярно действует на дугах (то есть на ребрах, которые считаются имеющими направление). [5]
Характеристический полином графа F26A равен
Другие объекты недвижимости
[ редактировать ]Граф F26A можно встроить как киральное регулярное отображение. в торе с 13 шестиугольными гранями. Двойственный граф для этого вложения изоморфен графу Пэли порядка 13.
Галерея
[ редактировать ]- Хроматическое число графа F26A равно 2.
- Хроматический индекс графа F26A равен 3.
- Альтернативный рисунок графика F26A.
- F26Граф, вложенный в тор .
Ссылки
[ редактировать ]- ^ Jump up to: а б Вайсштейн, Эрик В. «Кубический симметричный граф» . Математический мир .
- ^ Jump up to: а б Кондер М. и Добчани П. «Трехвалентные симметричные графы до 768 вершин». Дж. Комбин. Математика. Комбинировать. Вычислить. 40, 41–63, 2002.
- ^ Ройл, данные G. F026A.
- ^ «Янь-Цюань Фэн и Джин Хо Квак, Кубические s-регулярные графы , стр. 67» (PDF) . Архивировано из оригинала (PDF) 26 августа 2006 г. Проверено 12 марта 2010 г.
- ^ Ян-Цюань Фэн и Джин Хо Квак, «Однорегулярные кубические графы порядка небольшого числа, умноженного на простое число или простой квадрат», J. Aust. Математика. Соц. 76 (2004), 345-356 [1] .





