Круги зала

Круги Холла (также известные как M-круги и N-круги ) представляют собой графический инструмент в теории управления, используемый для получения значений передаточной функции с обратной связью из графика Найквиста (или графика Николса ) соответствующей передаточной функции с обратной связью. . Круги Холла были введены в теорию управления Альбертом К. Холлом в его диссертации. ^[1]

Строительство

Рассмотрим замкнутую линейную систему управления с разомкнутой передаточной функцией, заданной передаточной функцией $G(s)$ и с единичным коэффициентом усиления в контуре обратной связи. Передаточная функция с обратной связью определяется выражением ${\textstyle T(s)={\frac {G(s)}{1+G(s)}}}$ .

Чтобы проверить стабильность T ( s ), можно использовать критерий устойчивости Найквиста с графиком Найквиста передаточной функции разомкнутого контура G ( s ). Однако обратите внимание, что только график Найквиста для G ( s ) не дает фактических значений T ( s ). Чтобы получить эту информацию из плоскости G(s), Холл предложил построить геометрическое положение точек в плоскости G ( s ) такое, что T ( s ) имеет постоянную величину, а также геометрическое место точек в G ( s) -плоскости. )-плоскость такая, что T ( s ) имеет постоянный фазовый угол.

Учитывая положительное действительное значение M, представляющее фиксированную величину и обозначающее G(s) через z , точки, удовлетворяющие $M=|T(s)|={\frac {|G(s)|}{|1+G(s)|}}={\frac {|z|}{|1+z|}}$ задаются точками z на плоскости G ( s что отношение расстояния между z и 0 и расстояния между z и -1 равно M. ) такими , Точки z, удовлетворяющие этому условию локуса, являются окружностями Аполлония , и это геометрическое положение известно в контексте систем управления как М-окружности .

Учитывая положительное действительное значение N, представляющее фазовый угол, точки, удовлетворяющие $N=\arg \left[{\frac {G(s)}{1+G(s)}}\right]=\arg[G(s)]-\arg[1+G(s)]=\arg[z]-\arg[1+z]$ задаются точками z на плоскости G ( s ) такими, что угол между -1 и z и угол между 0 и z постоянны. Другими словами, угол, противоположный отрезку линии между -1 и 0, должен быть постоянным. Это означает, что точки z, удовлетворяющие этому условию геометрического положения, являются дугами окружностей, ^[2] и этот локус известен в контексте систем управления как N-круги .

Использование

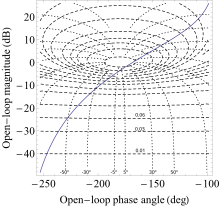
Чтобы использовать круги Холла, график M и N кругов строится поверх графика Найквиста передаточной функции разомкнутого контура. Точки пересечения этих графиков дают соответствующее значение передаточной функции замкнутого контура.

Круги Холла также используются с графиком Николса и в этом случае также известны как диаграмма Николса. Вместо непосредственного наложения кругов Холла на график Николса точки кругов переносятся в новую систему координат, где ордината определяется выражением $20\log _{10}(|G(s)|)$ а абсцисса определяется выражением $\arg(G(s))$ . Преимущество использования диаграммы Николса заключается в том, что регулировка усиления передаточной функции разомкнутого контура напрямую отражается на перемещении вверх и вниз графика Николса на диаграмме.

См. также

Примечания

^ К., Холл, Альберт (1943). Анализ и синтез линейных следящих механизмов . Кембридж: Technology Press, Массачусетский технологический институт. ISBN 9780262080736 . OCLC 857968901 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ «Жевание вписанных углов» . разрезать узел . Проверено 25 мая 2018 г.

Ссылки

Кацухико, Огата (2002). Современная техника управления (4-е изд.). Река Аппер-Седл, Нью-Джерси: Прентис-Холл. ISBN 0130609072 . OCLC 46619221 .
С., Найз, Норман (2008). Инженерия систем управления (5-е изд.). Хобокен, Нью-Джерси: Уайли. ISBN 9780471794752 . OCLC 154798791 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[1] К., Холл, Альберт (1943). Анализ и синтез линейных следящих механизмов . Кембридж: Technology Press, Массачусетский технологический институт. ISBN 9780262080736 . OCLC 857968901 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[2] «Жевание вписанных углов» . разрезать узел . Проверено 25 мая 2018 г.

[1]

[2]