Парадокс Линдли

Парадокс Линдли — это нелогичная ситуация в статистике , в которой байесовский и частотный подходы к проблеме проверки гипотез дают разные результаты для определенных вариантов априорного распределения . Проблема разногласий между двумя подходами обсуждалась в учебнике Гарольда Джеффриса 1939 года; это стало известно как парадокс Линдли после того, как Деннис Линдли назвал это разногласие парадоксом в статье 1957 года.

называются парадоксом Несмотря на то, что различия в результатах байесовского и частотного подходов , их можно объяснить тем, что они используются для ответа на фундаментально разные вопросы, а не фактическим разногласием между двумя методами.

Тем не менее, для большого класса априорных подходов различия между частотным и байесовским подходами вызваны сохранением фиксированного уровня значимости: как признавал даже Линдли, «теория не оправдывает практику сохранения фиксированного уровня значимости» и даже «некоторые вычисления Профессор Пирсон в обсуждении этой статьи подчеркнул, как уровень значимости должен был бы меняться в зависимости от размера выборки, если бы потери и априорные вероятности оставались фиксированными». Фактически, если критическое значение увеличивается с размером выборки достаточно быстро, то расхождение между частотным и байесовским подходами становится незначительным по мере увеличения размера выборки.

Парадокс продолжает оставаться источником активных дискуссий.

Описание парадокса

Результат $x$ некоторого эксперимента имеет два возможных объяснения – гипотезы $H_{0}$ и $H_{1}$ – и некоторое предварительное распределение $\pi$ представление неопределенности относительно того, какая гипотеза является более точной, прежде чем принимать во внимание $x$.

Парадокс Линдли возникает, когда

1. Результат $x$ является «значимым» по частотному критерию $H_{0},$ указывая достаточные доказательства для отклонения $H_{0},$ скажем, на уровне 5%, и
2. Апостериорная вероятность ​ $H_{0}$ данный $x$ высок, что указывает на убедительные доказательства того, что $H_{0}$ лучше согласуется с $x$ чем $H_{1}.$

Эти результаты могут возникнуть одновременно, когда $H_{0}$ очень специфичен, $H_{1}$ более размыты, и предыдущее распределение не сильно отдает предпочтение тому или другому, как показано ниже.

Численный пример

Следующий числовой пример иллюстрирует парадокс Линдли. В определенном городе за определенный период времени родился 49 581 мальчик и 48 870 девочек. Наблюдаемая доля $x$ рождений мужского пола, таким образом, составляет 451 ≈ 49 0,5036 581/98 . Мы предполагаем, что доля рождений мужского пола является биномиальной переменной с параметром $\theta .$ Мы заинтересованы в проверке того, $\theta$ составляет 0,5 или какое-либо другое значение. То есть наша нулевая гипотеза $H_{0}:\theta =0.5,$ и альтернатива $H_{1}:\theta \neq 0.5.$

Частотный подход

Частотный подход к тестированию $H_{0}$ состоит в том, чтобы вычислить p-значение , вероятность наблюдения за долей мальчиков, по крайней мере, такой же большой, как $x$ предполагая $H_{0}$ это правда. Поскольку число рождений очень велико, мы можем использовать нормальное приближение для доли рождений мужского пола. $X\sim N(\mu ,\sigma ^{2}),$ с $\mu =np=n\theta =98\,451\times 0.5=49\,225.5$ и $\sigma ^{2}=n\theta (1-\theta )=98\,451\times 0.5\times 0.5=24\,612.75,$ вычислить

${\begin{aligned}P(X\geq x\mid \mu =49\,225.5)=\int _{x=49\,581}^{98\,451}{\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {1}{2}}\left({\frac {u-\mu }{\sigma }}\right)^{2}}\,du\\=\int _{x=49\,581}^{98\,451}{\frac {1}{\sqrt {2\pi (24\,612.75)}}}e^{-{\frac {(u-49\,225.5)^{2}}{2\times 24\,612.75}}}\,du\approx 0.0117.\end{aligned}}$

Мы были бы столь же удивлены, если бы увидели 49 581 рождение девочек, т.е. $x\approx 0.4964,$ поэтому специалист по частоте обычно выполняет двусторонний тест, для которого значение p будет равно $p\approx 2\times 0.0117=0.0235.$ В обоих случаях значение p ниже уровня значимости α = 5%, поэтому частотный подход отвергает $H_{0},$ поскольку это не согласуется с наблюдаемыми данными.

Байесовский подход

Если предположить, что нет причин отдавать предпочтение одной гипотезе перед другой, байесовский подход будет заключаться в присвоении априорных вероятностей. $\pi (H_{0})=\pi (H_{1})=0.5$ и равномерное распределение по $\theta$ под $H_{1},$ а затем вычислить апостериорную вероятность $H_{0}$ используя теорему Байеса :

$P(H_{0}\mid k)={\frac {P(k\mid H_{0})\pi (H_{0})}{P(k\mid H_{0})\pi (H_{0})+P(k\mid H_{1})\pi (H_{1})}}.$

После наблюдения $k=49\,581$ мальчики из $n=98\,451$ рождений, мы можем вычислить апостериорную вероятность каждой гипотезы, используя функцию массы вероятности для биномиальной переменной:

${\begin{aligned}P(k\mid H_{0})&={n \choose k}(0.5)^{k}(1-0.5)^{n-k}\approx 1.95\times 10^{-4},\\P(k\mid H_{1})&=\int _{0}^{1}{n \choose k}\theta ^{k}(1-\theta )^{n-k}\,d\theta ={n \choose k}\operatorname {\mathrm {B} } (k+1,n-k+1)=1/(n+1)\approx 1.02\times 10^{-5},\end{aligned}}$

где $\operatorname {\mathrm {B} } (a,b)$ это бета-функция .

Из этих значений мы находим апостериорную вероятность $P(H_{0}\mid k)\approx 0.95,$ что решительно благоприятствует $H_{0}$ над $H_{1}$.

Два подхода — байесовский и частотный — кажутся конфликтующими, и в этом «парадокс».

Согласование байесовского и частотного подходов

Почти уверенная проверка гипотезы

Нееман предложил адаптацию уровня значимости к размеру выборки, чтобы контролировать ложноположительные результаты: α _n , так что α _n = n ^{− р} с г > 1/2 . По крайней мере, в числовом примере, если принять r = 1/2 , уровень значимости составит 0,00318, поэтому специалист по частоте не будет отвергать нулевую гипотезу, которая согласуется с байесовским подходом.

Неинформативные априоры

Распределение p при нулевой гипотезе и апостериорное распределение p

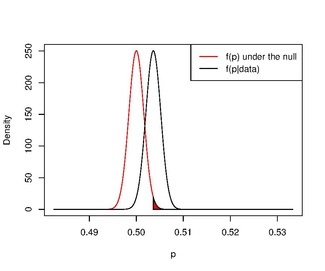
Если мы используем неинформативный априор и проверяем гипотезу, более похожую на гипотезу частотного подхода, парадокс исчезает.

Например, если мы вычислим апостериорное распределение $P(\theta \mid x,n)$, используя равномерное априорное распределение на $\theta$ (т.е. $\pi (\theta \in [0,1])=1$), мы находим

$P(\theta \mid k,n)=\operatorname {\mathrm {B} } (k+1,n-k+1).$

Если мы воспользуемся этим, чтобы проверить вероятность того, что новорожденный с большей вероятностью будет мальчиком, чем девочкой, т.е. $P(\theta >0.5\mid k,n),$ мы находим

$\int _{0.5}^{1}\operatorname {\mathrm {B} } (49\,582,48\,871)\approx 0.983.$

Другими словами, весьма вероятно, что доля рождений мужского пола превышает 0,5.

Ни один из анализов не дает непосредственной оценки размера эффекта , но оба могут быть использованы, например, для определения того, превысит ли доля рождений мальчиков какой-то конкретный порог.

Отсутствие настоящего парадокса

Кажущееся разногласие между двумя подходами вызвано сочетанием факторов. Во-первых, частотный подход выше тестов $H_{0}$ без ссылки на $H_{1}$. Байесовский подход оценивает $H_{0}$ как альтернатива $H_{1}$ и находит, что первое лучше согласуется с наблюдениями. Это связано с тем, что последняя гипотеза гораздо более расплывчата, поскольку $\theta$ может быть где угодно $[0,1]$, что приводит к очень низкой апостериорной вероятности. Чтобы понять почему, полезно рассмотреть две гипотезы как генераторы наблюдений:

• Под $H_{0}$, мы выбираем $\theta \approx 0.500$ и спросите, насколько вероятно появление 49 581 мальчика на 98 451 рождение.
• Под $H_{1}$, мы выбираем $\theta$ случайным образом из любого места в пределах от 0 до 1 и задайте тот же вопрос.

Большинство возможных значений для $\theta$ под $H_{1}$ очень плохо подтверждаются наблюдениями. По сути, кажущееся разногласие между методами — это вовсе не разногласие, а скорее два разных утверждения о том, как гипотезы соотносятся с данными:

• Частый пользователь обнаруживает, что $H_{0}$ является плохим объяснением наблюдения.
• Байесианцы считают, что $H_{0}$ является гораздо лучшим объяснением наблюдения, чем $H_{1}.$

Соотношение полов новорожденных, по данным частотного теста, неправдоподобно 50/50 мужской/женский. Однако соотношение 50/50 является лучшим приближением, чем большинство, но не все другие соотношения. Гипотеза $\theta \approx 0.504$ соответствовало бы наблюдению гораздо лучше, чем почти все другие соотношения, включая $\theta \approx 0.500.$

Например, этот выбор гипотез и априорных вероятностей подразумевает утверждение «если $\theta$ > 0,49 и $\theta$ < 0,51, то априорная вероятность $\theta$ ровно 0,5 составляет 0,50/0,51 ≈ 98%». Учитывая такое сильное предпочтение $\theta =0.5,$ легко понять, почему байесовский подход благоприятствует $H_{0}$ перед лицом $x\approx 0.5036,$ хотя наблюдаемое значение $x$ ложь $2.28\sigma$ от 0,5. Отклонение более 2 σ от $H_{0}$ считается значимым в частотном подходе, но его значение отменяется априорным в байесовском подходе.

Глядя на это с другой стороны, мы видим, что априорное распределение по существу плоское с дельта-функцией при $\theta =0.5.$ Понятно, что это сомнительно. Фактически, представляя действительные числа как непрерывные, было бы более логично предположить, что любое данное число не может быть в точности значением параметра, т. е. мы должны предположить, что $P(\theta =0.5)=0.$

Более реалистичное распределение для $\theta$ в альтернативной гипотезе дает менее неожиданный результат для задней части $H_{0}.$ Например, если мы заменим $H_{1}$ с $H_{2}:\theta =x,$ т.е. оценка максимального правдоподобия для $\theta ,$ апостериорная вероятность $H_{0}$ будет всего 0,07 по сравнению с 0,93 для $H_{2}$ (конечно, на самом деле нельзя использовать MLE как часть предыдущего дистрибутива).

См. также

• Байесовский фактор

Дальнейшее чтение

• Шафер, Гленн (1982). «Парадокс Линдли». Журнал Американской статистической ассоциации . 77 (378): 325–334. дои : 10.2307/2287244 . JSTOR   2287244 . МР   0664677 .