Парадокс вращения монеты


Парадокс вращения монеты — это парадоксальная математическая задача, заключающаяся в том, что, когда одна монета катится по краю другой монеты такого же размера, движущаяся монета совершает не один, а два полных оборота после полного оборота вокруг неподвижной монеты, если смотреть из внешней системы отсчета. [1] Проблему можно распространить на монеты разного радиуса.
Описание
[ редактировать ]Начните с двух одинаковых монет, соприкасающихся друг с другом на столе, причем их «головные» стороны отображаются параллельно. Удерживая монету А неподвижной, вращайте монету В вокруг А, сохраняя точку соприкосновения без проскальзывания. Когда монета B достигнет противоположной стороны, две орлы снова окажутся параллельными; B совершил один оборот. Продолжая движение, B возвращает его в исходное положение и совершает второй оборот. Парадоксально, но монета B, похоже, прокатилась на расстояние, равное удвоенной ее окружности. [2] : 220 В действительности, поскольку окружности обеих монет равны, монета B по определению прокатилась только на расстояние, равное ее собственной окружности. Второе вращение возникает из-за того, что путь, по которому он катился, представляет собой круг. Это аналогично простому вращению монеты B «на месте».
Один из способов визуализировать эффект — представить окружность монеты А «сплющенной» в прямую линию. Таким образом, можно наблюдать, что монета Б повернулась только один раз, когда она двигалась по своей, теперь уже плоской, траектории. Это «первая ротация». Точно так же скольжение монеты B по окружности монеты A вместо ее катания, сохраняя при этом ее текущую конкретную точку контакта, придаст вращение, характерное для «второго вращения» в исходном сценарии.
При вращении монеты B каждая точка ее периметра описывает (перемещается) кардиоидную кривую.
Анализ и решение
[ редактировать ]От начала до конца центр движущейся монеты движется по круговой траектории. Окружность неподвижной монеты и путь центра образуют два концентрических круга. Радиус внешнего круга представляет собой сумму радиусов монет; следовательно, длина окружности траектории движущегося центра в два раза больше окружности любой монеты. [3] Центр движущейся монеты проходит дважды по окружности монеты, не скользя; следовательно, движущаяся монета делает два полных оборота. [4]
Насколько движущаяся монета вращается вокруг своего центра в пути, если таковая имеется, или в каком направлении – по часовой стрелке, против часовой стрелки или в обоих направлениях – не влияет на длину пути. То, что монета вращается дважды, как описано выше, и сосредоточение внимания на краю движущейся монеты, когда он касается неподвижной монеты, отвлекает внимание.
Неравные радиусы и другие формы
[ редактировать ]
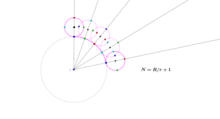
Монета радиуса r, катящаяся вокруг монеты радиуса R, делает R / r + 1 оборот. [5] Это происходит потому, что центр катящейся монеты движется по круговой траектории с радиусом (или окружностью) р + р / р = R / r + 1 раз собственный радиус (или окружность). В предельном случае, когда R = 0, монета радиуса r совершает 0 / r + 1 = 1 простое вращение вокруг своей нижней точки.
Форма, вокруг которой катится монета, не обязательно должна быть кругом: к отношению их периметров добавляется один дополнительный поворот, если это любой простой многоугольник или замкнутая кривая, не пересекающая сама себя. Если форма сложная , добавленное количество вращений (или вычтенное, если монета катится внутри кривой) является абсолютным значением числа ее поворотов .
Приложения
[ редактировать ]Звездное время
[ редактировать ]Парадокс связан со звездным временем : звездные сутки — это время, за которое Земля вращается, чтобы далекая звезда вернулась в то же положение на небе, тогда как солнечные сутки — это время, в течение которого Солнце возвращается в то же положение. В году около 36,5,25 солнечных дней, но . на один оборот вокруг Солнца приходится 36,6,25 сидерических дней [6] Поскольку солнечные сутки состоят из 24 часов, звездные сутки составляют около 365,25 / 366,25 × 24 часа = 23 часа 56 минут и 4,1 секунды.
Теория групп
[ редактировать ]Вариант загадки возникает в теории групп , в частности, при изучении группы Ли, известной как расщепленная вещественная форма G 2 . Одна из конструкций этой группы использует тот факт, что мяч, катящийся вокруг другого шара, радиус которого в три раза превышает его радиус, сделает четыре полных оборота, а не три. [7]
Ошибка оценки SAT 1982 года
[ редактировать ]1 мая 1982 года на одном из вступительных экзаменов в колледжи США, SAT , был задан вопрос с несколькими вариантами ответов, касающийся этой проблемы. Тест пришлось переоценить после того, как трое студентов доказали, что среди предложенных вариантов нет правильного ответа. [8] [9]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Вайсштейн, Эрик В. «Парадокс монеты» . Математический мир .
- ^ Паппас, Теони (1990). Радость математики: открывайте для себя математику повсюду . Сан-Карлос, Калифорния, ISBN 978-0-933174-65-8 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ Банч, Брайан Х. (1982). Математические заблуждения и парадоксы . Ван Ностранд Рейнхольд. стр. 10–11. ISBN 0-442-24905-5 .
- ^ «Динамика вращения - Центр колеса проходит длину окружности за один оборот» .
- ^ Талвалкар, Преш (5 июля 2015 г.). Все неправильно ответили на этот вопрос по математике на SAT . MindYourDecisions – через YouTube.
- ^ Бартлетт, А.К., Солнечное и звездное время , Popular Astronomy, vol. 12, стр.649-651
- ^ Баэз, Джон С .; Уэрта, Джон (2014). «G 2 и катящийся шар». Труды Американского математического общества . 366 (10): 5257–5293. arXiv : 1205.2447 . Бибкод : 2012arXiv1205.2447B . дои : 10.1090/S0002-9947-2014-05977-1 . МР 3240924 .
- ^ «В вопросе SAT обнаружена ошибка» . Нью-Йорк Таймс . Юнайтед Пресс Интернешнл. 25 мая 1982 г. ISSN 0362-4331 . Проверено 9 февраля 2021 г.
- ^ Мюллер, Дерек (30 ноября 2023 г.). Вопрос SAT: все ошибаются . Веритасиум – через YouTube.
Дальнейшее чтение
[ редактировать ]- Гарднер, Мартин (1975). «Пенни-пазлы». Математический карнавал . Альфред А. Кнопф.
Внешние ссылки
[ редактировать ]- Нгуен, Хуен (4 июня 2020 г.). «ответ на вопрос Какой доказанный математический факт вас больше всего удивил... » . Кура .
- Этот ответ, за который проголосовали, включает в себя анимацию и интуитивно понятные объяснения исходного вопроса, где r «внешней монеты» составляло 1/3 радиуса внутренней монеты.
- Мюллер, Дерек (30 ноября 2023 г.). Вопрос SAT: все ошибаются . Veritasium – через YouTube .