Парадокс колеса Аристотеля

Парадокс колеса Аристотеля — это парадокс или проблема, возникающая в псевдоаристотелевском греческом труде «Механика» . В нем говорится следующее: Колесо изображается в двумерном пространстве в виде двух кругов . Его больший внешний круг расположен по касательной к горизонтальной поверхности (например, дороге, по которой он катится), тогда как меньший, внутренний, имеет тот же центр и жестко прикреплен к большему. (Меньший круг может быть бортом шины, ободом, на котором она установлена, или осью.) Если предположить, что больший круг катится без проскальзывания (или заноса) в течение одного полного оборота, расстояния, пройденные окружностями обоих кругов, равны такой же. Расстояние, пройденное большим кругом, равно его длине , а для меньшего оно больше его окружности, тем самым создавая парадокс.

Парадокс не ограничивается колесами: другие предметы, изображенные в двух измерениях, демонстрируют такое же поведение, например, рулон ленты или типичная круглая бутылка или банка, перевернутая на бок (меньший круг будет горлышком или горлышком банки или бутылка).

В альтернативном варианте задачи с горизонтальной поверхностью соприкасается меньший круг, а не больший. Примеры включают обычное колесо поезда с фланцем или штангу, установленную на скамейке. Американский педагог и философ Исраэль Драбкин назвал эти варианты парадокса в случае II: ^{[ 1 ]} и применяется аналогичный, но неидентичный анализ.

История парадокса

В древности

В древности проблема колеса была описана в греческом труде «Механика» , традиционно приписываемом Аристотелю, но широко распространено мнение, что он был написан более поздним членом его школы. ^{[ 2 ]} (Томас Винтер выдвинул альтернативное предположение, что оно было написано Архитом . ^{[ 3 ]}) Он также появляется в Механике Героя Александрийского . ^{[ 1 ]}^{[ 4 ]} В аристотелевской версии это выглядит как «Задача 24», где описание колеса дается следующим образом:

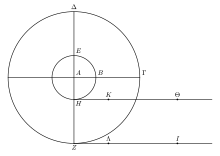
Схема колеса Аристотеля, описанная в *«Механике»* .

Пусть существует больший круг $ΔZΓ$ , меньший $EHB$ и $A$ в центре обоих; пусть $ZI$ — линия, которую больший разворачивает сам по себе, а $HK$ — линия, которую разворачивает сам по себе меньший, равная $ZΛ$ . Когда я перемещаю меньший круг, я перемещаю тот же центр, то есть $А$ ; пусть больший будет прикреплен к нему. Когда $AB$ становится перпендикулярным $HK$ , в то же время $AΓ$ становится перпендикулярным $ZΛ$ , так что он всегда проходит равное расстояние, а именно $HK$ для окружности $HB$ и $ZΛ$ для $ZΓ$ . Если четверть развернётся на равное расстояние, то ясно, что весь круг развернётся на равное расстояние всему кругу, так что, когда линия $BH$ дойдет до $K$ , окружность $ZΓ$ станет $ZΛ$ , и весь круг будет развёрнут. Точно так же, когда я передвигаю большой круг, подгоняя к нему малый, с одинаковым центром, то $AB$ будет перпендикулярно и под прямым углом одновременно с $AΓ$ , последний с $ZI$ , первый с $HΘ$ . Так что, когда тот завершит строку, равную $HΘ$ , а другой к $ZI$ , и $ZA$ становится снова перпендикулярным к $ZΛ$ , а $к$ HK $,$ так что они будут, как вначале, у $Θ$ и $I.$ НА ^{[ 5 ]}

Затем формулируется проблема:

А так как нет остановки большего для меньшего, так что оно [большое] остается в течение некоторого времени в одной и той же точке, и так как меньшее не перескакивает ни через какую точку, то странно, что большее проходит путь равен пути меньшего, и опять же, что меньшее проходит путь, равный пути большего. Примечательно также, что, хотя в каждом случае происходит только одно движение, перемещаемый центр в одном случае катится на большое расстояние, а в другом на меньшее. ^{[ 1 ]}

В научной революции

Математик Джероламо Кардано обсуждает проблему колеса в своем Opus novum deпропорциибус нумерорум 1570 года : ^{[ 6 ]} оспаривая презумпцию его анализа с точки зрения движения. ^{[ 1 ]} Мерсенн далее обсуждал это в своем Quaestiones Celeberrimae in Genesim 1623 года . ^{[ 7 ]} где он предполагает, что проблему можно проанализировать посредством процесса расширения и сжатия двух кругов. Но Мерсенн остался неудовлетворенным его пониманием и написал:

В самом деле, мне никогда не удавалось обнаружить, и я не думаю, что кто-либо еще мог обнаружить, касается ли меньший круг одной и той же точки дважды или движется скачками и скольжением. ^{[ 1 ]}

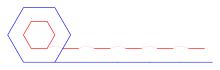
В своих «Двух новых науках » Галилей использует проблему колеса, чтобы привести доводы в пользу определенного вида атомизма . Он начинает свой анализ с рассмотрения пары концентрических шестиугольников , а не кругов. Представляя себе этот шестиугольник «катывающимся» по поверхности, Галилей замечает, что внутренний шестиугольник «перепрыгивает» на небольшое пространство при каждом перекатывании внешнего на новую грань. ^{[ 8 ]} Затем он представляет, что произойдет до предела, когда количество граней в многоугольнике станет очень большим, и обнаружит, что небольшое пространство, которое «перепрыгивает» внутренний многоугольник, становится все меньше и меньше. Он пишет:

Поэтому больший многоугольник, имеющий тысячу сторон, проходит и измеряет прямую, равную его периметру, в то время как меньший проходит примерно равную линию, но прерывисто составленную из тысячи маленьких частиц, равных тысяче его сторон, с между ними расположены тысячи маленьких пустот — ибо мы можем назвать их «пустотой» по отношению к тысячам линий, которых касаются стороны многоугольника. ^{[ 8 ]}

Поскольку круг — это всего лишь предел, в котором число граней многоугольника становится бесконечным, Галилей находит, что колесо Аристотеля содержит материал, заполненный бесконечно малыми пространствами или «пустотами», и что «между пустотами не поддаются количественному измерению, но они бесконечно велики». много". ^{[ 8 ]} Это приводит его к выводу, что веры в атомы – в том смысле, что материя «состоит из бесконечного множества неизмеримых атомов» – достаточно, чтобы объяснить это явление. ^{[ 8 ]} Жиль де Роберваль С этим анализом связан и (1602–1675).

В 19 веке

Бернар Больцано обсуждал колесо Аристотеля в «Парадоксах бесконечного» (1851 г.), книге, которая повлияла на Георга Кантора и последующих мыслителей о математике бесконечности. Больцано отмечает, что между точками любых двух подобных дуг существует биекция , которую можно реализовать, нарисовав радиус, отмечая, что история этого, казалось бы, парадоксального факта восходит к Аристотелю. ^{[ 1 ]}

В 20 веке

Автор книги «Математические заблуждения и парадоксы» использует десятицентовик, приклеенный к полудоллару (представляющий круги меньшего и большего размера соответственно) с выровненными центрами и прикрепленными к оси, в качестве модели парадокса. Он пишет:

Итак, это решение или ключ к нему. Хотя вы стараетесь не позволить полдоллара соскользнуть на стол, «точка», очерчивающая отрезок линии у подножия десятицентовой монеты, все время одновременно вращается и скользит. Он скользит относительно столешницы. Поскольку десятицентовая монета не касается столешницы, вы не заметите ее скольжения. Если вы можете катить полдоллара по столу и в то же время катить десятицентовую монету (или, еще лучше, ось) по деревянному бруску, вы действительно можете наблюдать скольжение. Если вы когда-либо припарковались слишком близко к бордюру, вы заметили визг, издаваемый колпаком вашей ступицы, когда он скользит (и катится) по бордюру, в то время как ваша шина просто катится по тротуару. Чем меньше маленький круг относительно большого, тем больше скользит маленький. Конечно, центр двух кругов вообще не вращается, поэтому скользит до конца. ^{[ 9 ]}

Анализ и решения

Парадокс заключается в том, что меньший внутренний круг перемещается на $2π R$ , окружность большего внешнего круга с радиусом $R$ , а не свою собственную окружность. Если бы внутренний круг катился отдельно, он переместился бы на $2π r$ , свою собственную окружность с радиусом $r$ . Внутренний круг не обособлен, а жестко связан с большим.

Первое решение

Если меньший круг зависит от большего (случай I), движение большего круга заставляет меньший пересекать окружность большего. Если больший круг зависит от меньшего (случай II), то движение меньшего круга заставляет больший круг пересекать окружность меньшего круга. Это самое простое решение.

Второе решение

Данное решение учитывает переход от стартовой позиции к конечной. Пусть $Pb$ — точка на большем круге, а $Ps$ — точка на меньшем круге, причем обе точки имеют одинаковый радиус. Для удобства предположим, что они оба находятся прямо под центром, аналогично обеим стрелкам часов, указывающим на шесть. И $Pb$ , и $Ps$ движутся по циклоиде , совершая один оборот. ^{[ 10 ]}

Хотя каждый из них проходит $2π R$ по горизонтали от начала до конца, $циклоидный путь Ps$ короче и эффективнее, чем $у Pb$ . $Pb$ перемещается выше и ниже пути центра – единственного прямого – чем $Ps$ .

Если бы $Pb$ и $Ps$ находились где-нибудь еще на своих кругах, изогнутые пути были бы одинаковой длины. Подводя итог, можно сказать, что меньший круг движется горизонтально на $2π R,$ потому что любая точка на меньшем круге движется по более короткому и, следовательно, более прямому пути, чем любая точка на большом круге.

См. также

Ссылки

^ Перейти обратно: ^а ^б ^с ^д ^и ^ж Драбкин, Израиль Э. (1950). «Колесо Аристотеля: заметки по истории парадокса». Осирис . 9 : 162–198. дои : 10.1086/368528 . JSTOR 301848 . S2CID 144387607 .
^ Хит, Томас Литтл (2003) [1931]. Руководство по греческой математике . Минеола, Нью-Йорк: Dover Publications. п. 199. ИСБН 978-0486432311 .
^ Томас Нельсон Винтер, « Механические проблемы в корпусе Аристотеля », DigitalCommons@University of Nebraska – Lincoln, 2007.
^ «Цапля Александринская Механическая» . Перевод Миллера, Ютта. 1999. Задача 7 . Проверено 27 июля 2023 г.
^ Леувен, Джойс ван (17 марта 2016 г.). Аристотелевская механика: текст и диаграммы . Спрингер. ISBN 9783319259253 .
^ Кардано, Джеронимо (1570). Новая работа о пропорциях чисел...: Помимо великого искусства или алгебраических правил, одна книга... Еще и о книге правил...
^ Мерсенн, Марин (1623). Самые известные вопросы в Бытии... (на латыни).
^ Перейти обратно: ^а ^б ^с ^д Галилей, Галилей; Дрейк, Стиллман (2000). Две новые науки: включая центры гравитации и силу удара . Уолл и Эмерсон. ISBN 9780921332503 .
^ Банч, Брайан Х. (1982). Математические заблуждения и парадоксы . Ван Ностранд Рейнхольд. стр. 3–9. ISBN 0-442-24905-5 .
^ Здесь изображены два пути: http://mathworld.wolfram.com/Cycloid.html и http://mathworld.wolfram.com/CurtateCycloid.html.

Дальнейшее чтение

Хаттон, Чарльз (1795). « Рота Аристотелика » . Математико-философский словарь . Том. 2. п. 398. Архивировано из оригинала 02 июля 2017 г.
Вайсштейн, Эрик В. «Парадокс колеса Аристотеля» . Математический мир .

[:0-1] Перейти обратно: ^а ^б ^с ^д ^и ^ж Драбкин, Израиль Э. (1950). «Колесо Аристотеля: заметки по истории парадокса». Осирис . 9 : 162–198. дои : 10.1086/368528 . JSTOR 301848 . S2CID 144387607 .

[2] Хит, Томас Литтл (2003) [1931]. Руководство по греческой математике . Минеола, Нью-Йорк: Dover Publications. п. 199. ИСБН 978-0486432311 .

[3] Томас Нельсон Винтер, « Механические проблемы в корпусе Аристотеля », DigitalCommons@University of Nebraska – Lincoln, 2007.

[4] «Цапля Александринская Механическая» . Перевод Миллера, Ютта. 1999. Задача 7 . Проверено 27 июля 2023 г.

[5] Леувен, Джойс ван (17 марта 2016 г.). Аристотелевская механика: текст и диаграммы . Спрингер. ISBN 9783319259253 .

[6] Кардано, Джеронимо (1570). Новая работа о пропорциях чисел...: Помимо великого искусства или алгебраических правил, одна книга... Еще и о книге правил...

[7] Мерсенн, Марин (1623). Самые известные вопросы в Бытии... (на латыни).

[:1-8] Перейти обратно: ^а ^б ^с ^д Галилей, Галилей; Дрейк, Стиллман (2000). Две новые науки: включая центры гравитации и силу удара . Уолл и Эмерсон. ISBN 9780921332503 .

[9] Банч, Брайан Х. (1982). Математические заблуждения и парадоксы . Ван Ностранд Рейнхольд. стр. 3–9. ISBN 0-442-24905-5 .

[10] Здесь изображены два пути: http://mathworld.wolfram.com/Cycloid.html и http://mathworld.wolfram.com/CurtateCycloid.html.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]