Аристотелевская реалистическая философия математики
В философии математики , аристотелевский реализм утверждает, что математика изучает такие свойства, как симметрия , непрерывность и порядок которые могут быть имманентно реализованы в физическом мире (или в любом другом мире, который может существовать). Он контрастирует с платонизмом, утверждая, что объекты математики, такие как числа, не существуют в «абстрактном» мире, но могут быть физически реализованы. [1] Он контрастирует с номинализмом , фикционализмом и логицизмом, утверждая, что математика — это не просто имена или методы вывода или вычислений, а определенные реальные аспекты мира.
Аристотелевские реалисты подчеркивают, что прикладная математика , особенно математическое моделирование , а не чистая математика, является наиболее важной с философской точки зрения. Марк Ланге утверждает, что «аристотелевский реализм позволяет математическим фактам быть объяснениями в чисто математических объяснениях» в науке, поскольку сами математические факты касаются физического мира. [2] Пол Тагард описывает аристотелевский реализм как «современную философию математики, которая лучше всего соответствует тому, что известно о сознании и науке ». [3]
История [ править ]
Хотя Аристотель не писал много о философии математики, его различные замечания по этой теме демонстрируют последовательный взгляд на этот предмет как на абстракции, так и на применимый к реальному миру пространства и счета. [4] До восемнадцатого века наиболее распространенной философией математики была аристотелевская точка зрения, согласно которой это «наука о количестве », в которой количество делится на непрерывное (изучаемое геометрией ) и дискретное (изучаемое арифметикой). [5]
Аристотелевские подходы к философии математики были редкостью в двадцатом веке, но были возрождены Пенелопой Мэдди в «Реализме в математике» (1990), а также рядом авторов с 2000 года, таких как Джеймс Франклин , [6] Энн Ньюстед, [7] Дональд Гиллис и другие.
Числа и множества [ править ]
Аристотелевские взгляды на числа ( кардинальные или счетные) начинаются с наблюдения Аристотеля о том, что число кучи или совокупности зависит от выбранной единицы или меры: «число» означает измеренное множество и множество мер... мера всегда должна быть какой-то идентичной вещью, которую можно предсказать обо всех вещах, которые она измеряет, например, если эти вещи — лошади, то мерой является «лошадь». [8] Гленн Кесслер развивает это мнение, что число — это отношение между кучей и универсалией , которая делит ее на единицы; например, число 4 реализуется в отношении между кучей попугаев и универсальным «быть попугаем», которое делит кучу на такое-то количество попугаев. [9] [10] [5] : 36–8
С точки зрения Аристотеля, отношения не связаны тесно с кардинальными числами. Это отношения между такими величинами, как высоты. Отношение двух высот может быть таким же, как отношение между двумя массами или двумя интервалами времени. [5] : 34–5
Аристотелианцы считают множества, как и числа, воплощенными в физическом мире (а не платонистскими сущностями). Мэдди утверждала, что когда открывается коробка с яйцами, воспринимается набор из трех яиц (то есть математическая сущность, реализованная в физическом мире). [11] Однако не весь математический дискурс необходимо интерпретировать реалистично; например, сторонники Аристотеля могут рассматривать пустое множество и ноль как фикции, [5] : 234–40 и, возможно, более высокие бесконечности.
Структурные свойства [ править ]
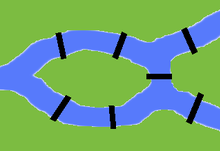
Сторонники Аристотеля считают нечисловые структурные свойства, такие как симметрия, непрерывность и порядок, столь же важными, как и числа. Такие свойства реализуются в физической реальности и являются предметом некоторых разделов математики. Например, теория групп классифицирует различные виды симметрии, а исчисление изучает непрерывные вариации. Доказуемые результаты о таких структурах могут быть применимы непосредственно к физической реальности. Например, Эйлер доказал, что невозможно пройти один и только один раз по семи мостам Кенигсберга . [5] : 48–56
Эпистемология [ править ]
Поскольку математические свойства реализуются в физическом мире, их можно непосредственно воспринимать. Например, люди легко воспринимают симметрию лица .
Аристотелианцы также отводят роль абстракции и идеализации в математическом мышлении. Эта точка зрения восходит к заявлению Аристотеля в его «Физике» о том, что разум «выделяет» в мыслях свойства, которые он изучает в математике, рассматривая вневременные свойства тел отдельно от мира изменений (Физика II.2.193b31-35).
На более высоких уровнях математики сторонники Аристотеля следуют теории апостериорной аналитики Аристотеля , согласно которой доказательство математического утверждения в идеале позволяет читателю понять, почему это предложение должно быть истинным. [5] : 192–6
против аристотелевского Возражения реализма
Проблема аристотелевского реализма заключается в том, как объяснить высшие бесконечности , которые могут быть не реализованы или нереализуемы в физическом мире. Аристотеля Как применить теорию потенциальности и актуальности к теории множеств Цермело – Франкеля . [ объяснить ] Марк Балагер пишет:
- «Теория множеств привержена существованию бесконечных множеств, которые настолько огромны, что они просто затмевают разнообразные бесконечные множества, такие как множество всех натуральных чисел. Просто не существует правдоподобного способа интерпретировать этот разговор о гигантских бесконечных множествах как о физические объекты». [12]
Аристотелианцы отвечают, что науки могут иметь дело с неконкретизированными универсалиями; например, наука о цвете может иметь дело с оттенком синего, который не встречается ни на одном реальном объекте. [13] Однако для этого необходимо отрицать принцип реализации , которого придерживается большинство сторонников Аристотеля, который утверждает, что все подлинные свойства реализуются. Одним из аристотелевских философов математики, который отрицает принцип реализации на основе проведенного Фреге различия между смыслом и референцией, является Дональд Гиллис . Он использовал этот подход для разработки метода работы с очень большими трансфинитными кардиналами с аристотелевской точки зрения. [14]
Другое возражение против аристотелизма состоит в том, что математика имеет дело с идеализацией физического мира, а не с самим физическим миром. Сам Аристотель знал об аргументе, что геометры изучают идеальные круги, но обручи в реальном мире не являются идеальными кругами, поэтому кажется, что математика, должно быть, изучает некий нефизический (платоновский) мир. [15] Сторонники Аристотеля отвечают, что прикладная математика изучает приближения, а не идеализации, и в результате современная математика может изучать сложные формы и другие математические структуры реальных вещей. [5] : 225–9 [16]
Ссылки [ править ]
- ^ Франклин, Джеймс (7 апреля 2014 г.). «Математический мир» . Эон . Проверено 30 июня 2021 г.
- ^ Ланге, Марк (2021). «Чем может быть математика, чтобы она могла функционировать в чисто математических научных объяснениях?» . Исследования по истории и философии науки А. 87 : 44–53. Бибкод : 2021ШПСА..87...44Л . дои : 10.1016/j.shpsa.2021.02.002 . ПМИД 34111822 . S2CID 233545723 . Проверено 30 июня 2021 г.
- ^ Тагард, Пол (2019). Натуральная философия: от социального мозга к знанию, реальности, морали и красоте . Нью-Йорк: Издательство Оксфордского университета. п. 442. ИСБН 9780190686444 .
- ^ Босток, Д. (16 августа 2012 г.). «Философия математики Аристотеля». В Шилдс, CJ (ред.). Оксфордский справочник Аристотеля . Оксфорд: Издательство Оксфордского университета. ISBN 9780195187489 .
- ^ Jump up to: Перейти обратно: а б с д и ж г Франклин, Джеймс (2014). Аристотелевская реалистическая философия математики: математика как наука о количестве и структуре . Бейзингсток: Пэлгрейв Макмиллан. п. 123. ИСБН 9781137400727 .
- ^ Франклин, Джеймс (2022). «Математика как наука о неабстрактной реальности: аристотелевская реалистическая философия математики» . Основы науки . 27 (2): 327–344. дои : 10.1007/s10699-021-09786-1 . S2CID 233658181 . Проверено 30 июня 2021 г.
- ^ AGJ Ньюстед, (2001). «Аристотель и современные математические теории континуума», в Д. Сфендони-Менцу, Дж. Хаттиангади и Д. М. Джонсоне (редакторы), «Аристотель и современная наука» , Питер Ланг, 113–129.
- ^ Аристотель, Метафизика 1088a4-11.
- ^ Кесслер, Гленн (1980). «Фреге, Милль и основы арифметики» . Журнал философии . 77 (2): 65–79. дои : 10.2307/2025431 . JSTOR 2025431 . Проверено 30 июня 2021 г.
- ^ Форрест, Питер ; Армстронг, DM (1987). «Природа числа» . Философские статьи . 16 (3): 165–186. дои : 10.1080/05568648709506275 . Проверено 30 июня 2021 г.
- ^ Мэдди, Пенелопа (1990). Реализм в математике . Оксфорд: Издательство Оксфордского университета. п. 58-67. ISBN 9780198240358 .
- ^ Балагер, Марк (2018). «Фикционализм в философии математики» . Стэнфордская энциклопедия философии . Проверено 30 июня 2021 г.
- ^ Франклин, Джеймс (2015). «Неконкретизированные свойства и полуплатонический аристотелизм» . Обзор метафизики . 69 :25–45 . Проверено 29 июня 2021 г.
- ^ Гиллис, Дональд (2015). «Аристотелевский подход к математической онтологии». В Дэвисе, Эрнест; Дэвис, Филип Дж. (ред.). Математика, вещество и предположение . Чам: Спрингер. стр. 147–176. ISBN 9783319214726 .
- ^ Аристотель, Метафизика 997b35-998a4.
- ^ А.Ньюстед, Дж. Франклин (2009). «Эпистемология геометрии I: проблема точности», ASCS09, Труды 9-й конференции Австралазийского общества когнитивных наук , Сидней, 254–260, статья DOI: 10.5096/ASCS200939.
Библиография [ править ]
- Джон Бигелоу, 1988, Реальность чисел , Кларендон, Оксфорд, ISBN 9780198249573
- Джеймс Франклин, 2014, Аристотелевская реалистическая философия математики: математика как наука о количестве и структуре , Пэлгрейв Макмиллан, Бейзингсток, ISBN 9781137400727 .
- Кейт Хоссак, 2020, « Знание и философия чисел: что такое числа и как они известны» , Блумсбери, Лондон, ISBN 9781350102927
- Эндрю Ирвин , 1990. Физикализм в математике , Дордрехт, Лондон, ISBN 9780792305132
- Боб Кнапп, 2014, «Математика о мире» , Лексингтон, Кентукки, ISBN 9781500551971
- Пенелопа Мэдди, 1990, Реализм в математике , Oxford University Press, Нью-Йорк, ISBN 9780198240358
- Вусук Парк, 2018, Утрата логики философии в математике , Спрингер, Чам, ISBN 9783319951461
- Эндрю Юнан, 2022, Материя и математика: эссенциалистский взгляд на законы природы , Издательство Католического университета Америки, Вашингтон, округ Колумбия, ISBN 9780813236124