Разделитель вершин

В теории графов вершин подмножество ⁠ $S\subset V$ ⁠ — разделитель вершин (или разрез вершин , разделяющее множество ) для несмежных вершин $a$ и $b$ если удаление S $,$ из графа разделяет $a$ и $b$ на отдельные компоненты связности .

Примеры

Рассмотрим сеточный граф с $r$ строками и $c$ столбцами; общее количество $n$ вершин $равно r \times c$ . Например, на иллюстрации $r = 5$ , $c = 8$ и $n = 40$ . Если $r$ нечетно, существует одна центральная строка, в противном случае есть две строки, одинаково близкие к центру; аналогично, если $c$ нечетно, существует один центральный столбец, в противном случае есть два столбца, одинаково близких к центру. Выбор $S$ в качестве любой из этих центральных строк или столбцов и удаление $S$ из графа разбивает граф на два меньших связных подграфа $A$ и $B$ , каждый из которых имеет не более $.mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}n ⁄ 2$ вершины. Если $r \leq c$ (как на рисунке), то выбор центрального столбца даст разделитель $S$ с $r\leq {\sqrt {n}}$ вершин, и аналогично, если $c \leq r$ , то выбор центральной строки даст разделитель с не более чем ${\sqrt {n}}$ вершины. Таким образом, каждый сеточный граф имеет разделитель $S$ размера не более ${\sqrt {n}},$ удаление которого разбивает его на две связные компоненты, каждая размером не более $n ⁄ 2$ . ^[1]

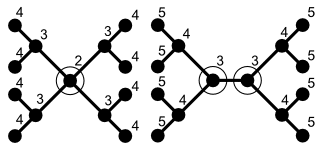
Слева центрированное дерево, справа бицентрическое. Числа показывают эксцентриситет каждого узла.

Приведем еще один класс примеров: каждое свободное дерево $T$ имеет разделитель $S,$ состоящий из одной вершины, удаление которого разбивает $T$ на две или более компоненты связности, каждая из которых имеет размер не более $п ⁄ 2$ . Точнее, всегда существует ровно одна или ровно две вершины, составляющие такой разделитель, в зависимости от того, центрировано или бицентрировано дерево . ^[2]

В отличие от этих примеров, не все вершинные разделители сбалансированы , но это свойство наиболее полезно для приложений в информатике, таких как теорема о плоском сепараторе .

Минимальные разделители

Пусть $S$ — $(a, b)$ -разделитель, то есть подмножество вершин, разделяющее две несмежные вершины $a$ и $b$ . Тогда $S$ является минимальным $(a, b)$ -сепаратором , если никакое собственное подмножество $S$ не разделяет $a$ и $b$ . В более общем смысле $S$ называется минимальным сепаратором , если он является минимальным сепаратором для некоторой пары $(a, b)$ несмежных вершин. Обратите внимание, что это отличается от минимального разделяющего множества , в котором говорится, что ни одно собственное подмножество $S$ не является минимальным $(u, v)$ -разделителем для любой пары вершин $(u, v)$ . Следующий хорошо известный результат, характеризующий минимальные сепараторы: ^[3]

Лемма. Вершинный разделитель $S$ в $G$ является минимальным тогда и только тогда, когда граф $G - S$ , полученный удалением $S$ из $G$ , имеет две компоненты связности $C 1$ и $C 2$ такие, что каждая вершина в $S$ одновременно смежна с некоторой вершиной из $C 1$ и в некоторую вершину в $C 2$ .

Минимальные $(a, b)$ -сепараторы также образуют алгебраическую структуру : для двух фиксированных вершин $a$ и $b$ данного графа $G$ -сепаратор $(a, b)$ -сепаратора $S$ можно рассматривать как предшественник другого $(a, b)$ . -разделитель $T$ , если каждый путь от $a$ до $b$ встречает $S$ как он встретит $T.$ до того , Более строго отношение предшественника определяется следующим образом: Пусть $S$ и $T$ два $(a, b)$ -разделителя в $G.$ — Тогда $S$ является предшественником $T$ в символах $S\sqsubseteq _{a,b}^{G}T$ , если для каждого $x ∈ S \ T$ каждый путь, соединяющий $x$ с $b,$ пересекает $T$ . Из определения следует, что отношение предшественника дает предварительный порядок на множестве всех $(a, b)$ -разделителей. Более того, Эскаланте (1972) доказал, что отношение предшественника порождает полную решетку если ограничиться набором минимальных $(a, b)$ -сепараторов в $G.$ ,

См. также

Хордальный граф — граф, в котором каждый минимальный разделитель является кликой .
k-связный граф

Примечания

^ Джордж (1973) . Вместо использования строки или столбца сеточного графика Джордж разбивает график на четыре части, используя объединение строки и столбца в качестве разделителя.
^ Джордан (1869)
^ Голуббик (1980) .

Ссылки

Эскаланте, Ф. (1972). «Разрезание решеток в графах». Трактаты математического семинара Гамбургского университета . 38 : 199-220. дои : 10.1007/BF02996932 .
Джордж, Дж. Алан (1973), «Вложенное рассечение регулярной сетки конечных элементов», SIAM Journal on Numerical Analysis , 10 (2): 345–363, Бибкод : 1973SJNA...10..345G , doi : 10.1137/ 0710032 , JSTOR 2156361 .
Голумбик, Мартин Чарльз (1980), алгоритмическая теория графов и совершенные графы , Academic Press, ISBN 0-12-289260-7 .
Джордан, Камилла (1869). «Сюр-ле-сборки линий» . Журнал чистой и прикладной математики (на французском языке). 70 (2): 185–190.
Розенберг, Арнольд ; Хит, Ленвуд (2002). Разделители графов с приложениями . Границы информатики. Спрингер. дои : 10.1007/b115747 . ISBN 0-306-46464-0 .

[g73-1] Джордж (1973) . Вместо использования строки или столбца сеточного графика Джордж разбивает график на четыре части, используя объединение строки и столбца в качестве разделителя.

[Jordan-2] Джордан (1869)

[3] Голуббик (1980) .

[1]

[2]

[3]