Строковый граф
В теории графов струнный граф — это граф пересечения кривых на плоскости ; каждая кривая называется «струной». Учитывая граф G , G является строковым графом тогда и только тогда, когда существует набор кривых или строк, такой, что граф, имеющий для каждой кривой и ребро для каждой пересекающейся пары кривых изоморфен G. , вершину
Фон
[ редактировать ]Сеймур Бензер ( 1959 ) описал концепцию, аналогичную строковым графам, применительно к генетическим структурам. В этом контексте он также изложил конкретный случай пересечения интервалов на прямой, а именно ставшее классическим семейство графов интервалов . Позже Синден (1966) применил ту же идею к электрическим сетям и печатным схемам. Математическое исследование строковых графов началось со статьи Эрлиха, Эвена и Тарьяна (1976) . благодаря сотрудничеству Синдена и Рональда Грэма , где характеристика строковых графов в конечном итоге стала открытым вопросом на 5-м венгерском коллоквиуме по комбинаторике в 1976 году. [1] Однако в конечном итоге было доказано, что распознавание строковых графов является NP-полным , а это означает, что простой характеризации, скорее всего, не существует. [2]
Связанные классы графов
[ редактировать ]
Каждый планарный граф представляет собой строковый граф: [3] можно сформировать представление строкового графа для произвольного графа, вложенного в плоскость, нарисовав для каждой вершины строку, которая огибает вершину и середину каждого смежного ребра, как показано на рисунке. Для любого ребра uv графа строки u и v пересекают друг друга дважды около середины uv , и других пересечений нет, поэтому пары пересекающихся строк представляют собой в точности соседние пары вершин исходного плоского графа. . В качестве альтернативы, согласно теореме об упаковке кругов , любой плоский граф может быть представлен как набор кругов, любые два из которых пересекаются тогда и только тогда, когда соответствующие вершины смежны; эти круги (с начальной и конечной точкой, выбранной для превращения их в разомкнутые кривые) обеспечивают представление данного плоского графа в виде строкового графа. Chalopin, Gonçalves & Ochem (2007) доказали, что каждый планарный граф имеет строковое представление, в котором каждая пара строк имеет не более одной точки пересечения, в отличие от представлений, описанных выше. Гипотеза Шайнермана , теперь доказанная, представляет собой еще более сильное утверждение о том, что каждый плоский граф может быть представлен графом пересечения отрезков прямых, что является особым случаем струн.
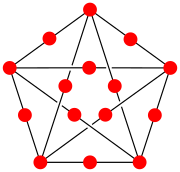
Если каждое ребро данного графа G подразделено , полученный граф является строковым графом тогда и только тогда, когда G планарен. В частности, подразделение полного графа K 5 , показанное на иллюстрации, не является строковым графом, поскольку K 5 не является плоским. [3]
Каждый круговой граф , как граф пересечений отрезков прямых (хорд окружности), также является строковым графом. Каждый хордальный граф может быть представлен как строковый граф: хордальные графы представляют собой графы пересечений поддеревьев деревьев, и можно сформировать строковое представление хордального графа, формируя планарное вложение соответствующего дерева и заменяя каждое поддерево строкой, которая отслеживает по краям поддерева.
Граф дополнений каждого графа сравнимости также является строковым графом. [4]
Другие результаты
[ редактировать ]Эрлих, Эвен и Тарьян (1976) показали, что вычисление хроматического числа строковых графов является NP-трудным. Краточвил (1991a) обнаружил, что строковые графы образуют индуцированный второстепенный закрытый класс, но не второстепенный закрытый класс графов.
Любой строковый граф с m -ребрами можно разделить на два подмножества, каждое из которых представляет собой постоянную долю размера всего графа, путем удаления O ( m 3/4 бревно 1/2 m ) вершины. Отсюда следует, что струнные графы без биклик , струнные графы, не содержащие подграфов Kt , полиномиальное t для некоторой константы t , имеют O ( n ) ребер и, более строго, имеют разложение . [5]
Примечания
[ редактировать ]- ^ Грэм (1976) .
- ^ Краточвил (1991b) показал, что распознавание строковых графов является NP-трудным, но не смог показать, что его можно решить в NP. После промежуточных результатов Шефера и Штефанковича (2001) и Паха и Тота (2002) , Шефер, Седжвик и Штефанкович (2003) завершили доказательство того, что задача NP-полна.
- ^ Jump up to: а б Шефер и Штефанкович (2001) приписывают это наблюдение Синдену (1966) .
- ^ Голумбик, Ротем и Уррутия (1983) и Ловас (1983) . См. также Fox & Pach (2010) .
- ^ Фокс и Пах (2010) ; Дворжак и Норин (2016) .
Ссылки
[ редактировать ]- Бензер, С. (1959), «О топологии тонкой генетической структуры», Труды Национальной академии наук Соединенных Штатов Америки , 45 (11): 1607–1620, Бибкод : 1959PNAS...45.1607B , doi : 10.1073/pnas.45.11.1607 , PMC 222769 , PMID 16590553 .
- Чалопин Дж.; Гонсалвес, Д.; Очем, П. (2007), «Плоские графы имеют 1-СТРУНУ», Труды восемнадцатого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам , ACM и SIAM, стр. 609–617 .
- Дворжак, Зденек ; Норин, Сергей (2016), «Сильно сублинейные сепараторы и полиномиальное разложение», SIAM Journal on Discrete Mathematics , 30 (2): 1095–1101, arXiv : 1504.04821 , Bibcode : 2015arXiv150404821D , doi : 10.1137/15M101756 9 .
- Эрлих, Г.; Эвен, С.; Тарьян, Р.Э. (1976), «Графики пересечения кривых на плоскости», Журнал комбинаторной теории , 21 (1): 8–20, doi : 10.1016/0095-8956(76)90022-8 .
- Фокс, Джейкоб ; Пах, Янош (2010), «Теорема о разделителе для строковых графов и ее приложения», Combinatorics, Probability and Computing , 19 (3): 371, doi : 10.1017/s0963548309990459 , S2CID 5705145 .
- Голуббич, М.; Ротем, Д.; Уррутиа, Дж. (1983), «Графы сопоставимости и графы пересечений», Discrete Mathematics , 43 (1): 37–46, doi : 10.1016/0012-365X(83)90019-5 .
- Грэм, Р.Л. (1976), «Проблема 1», Открытые проблемы на 5-м венгерском коллоквиуме по комбинаторике .
- Краточвил, Ян (1991a), «Струнные графы. I. Число критических неструнных графов бесконечно», Journal of Combinatorial Theory , Series B , 52 (1): 53–66, doi : 10.1016/0095-8956(91) 90090-7 .
- Краточвил, Ян (1991b), «Струнные графы. II. Распознавание строковых графов NP-сложно», Journal of Combinatorial Theory , Series B , 52 (1): 67–78, doi : 10.1016/0095-8956(91)90091 -В .
- Ловас, Л. (1983), «Идеальные графы», Избранные темы теории графов , том. 2, Лондон: Academic Press, стр. 55–87 .
- Пах, Янош ; Тот, Геза (2002), «Распознавание строковых графов разрешимо», Discrete & Computational Geometry , 28 (4): 593–606, doi : 10.1007/s00454-002-2891-4 .
- Шефер, Маркус; Штефанкович, Дэниел (2001), «Разрешимость строковых графов», Труды 33-го ежегодного симпозиума ACM по теории вычислений (STOC 2001) : 241–246 .
- Шефер, Маркус; Седжвик, Эрик; Штефанкович, Дэниел (2003), «Распознавание строковых графов в NP», Журнал компьютерных и системных наук , 67 (2): 365–380, doi : 10.1016/S0022-0000(03)00045-X .
- Синден, Ф.В. (1966), «Топология тонкопленочных RC-цепей», Технический журнал Bell System , 45 (9): 1639–1662, doi : 10.1002/j.1538-7305.1966.tb01713.x .