Анализ сетки

Анализ сетки (или метод тока сетки ) — это анализа метод плоских цепей . Плоские цепи — это цепи, которые можно нарисовать на плоской поверхности без пересечения проводов друг с другом. Более общий метод, называемый анализом контура (с соответствующими сетевыми переменными, называемыми токами контура ), может быть применен к любой цепи, плоской или нет. ^{[ нужна ссылка ]}. Анализ сетки и анализ контуров систематически используют закон напряжения Кирхгофа для получения набора уравнений, которые гарантированно будут разрешимы, если схема имеет решение. ^[1] Анализ сетки обычно проще использовать, когда схема плоская, по сравнению с анализом контура. ^[2]

Сеточные токи и существенные сетки

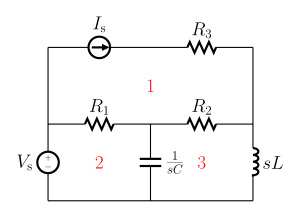
Анализ сетки работает путем произвольного назначения токов сетки в основных сетках (также называемых независимыми сетками). Существенная сетка — это петля в схеме, не содержащая других петель. На рисунке 1 основные сетки обозначены цифрами один, два и три. ^[3]

Ток сетки — это ток, который обтекает основную сетку, и уравнения решаются в их терминах. Сеточный ток может не соответствовать никакому физически текущему току, но по ним легко находятся физические токи. ^[2] Обычно все токи в сети имеют одно и то же направление. Это помогает предотвратить ошибки при написании уравнений. Соглашение заключается в том, чтобы все токи сетки вращались по часовой стрелке. ^[3] На рисунке 2 показана та же схема, что и на рисунке 1, с обозначением токов сетки.

Расчет токов сетки вместо прямого применения закона тока Кирхгофа и закона напряжения Кирхгофа может значительно сократить объем необходимых вычислений. Это связано с тем, что токов сетки меньше, чем токов физических ветвей. Например, на рисунке 2 имеется шесть токов ветвей, но только три токов сетки.

Настройка уравнений

Каждая сетка дает одно уравнение. Эти уравнения представляют собой сумму падений напряжения в полной петле тока сетки. ^[3] Для проблем более общего характера, чем те, которые включают источники тока и напряжения , падение напряжения будет равно импедансу электронного компонента, умноженному на ток сетки в этом контуре. ^[4]

Если источник напряжения в контуре сетки присутствует , напряжение на источнике либо добавляется, либо вычитается в зависимости от того, является ли это падением напряжения или повышением напряжения в направлении тока сетки. Для источника тока , который не находится между двумя сетками (например, источник тока в основной сетке 1 в схеме выше), ток сетки примет положительное или отрицательное значение источника тока в зависимости от того, находится ли ток сетки в в том же или противоположном направлении источника тока . ^[3] Ниже представлена та же схема, что и выше, с уравнениями, необходимыми для решения всех токов в цепи.

${\begin{cases}{\text{Mesh 1: }}I_{1}=I_{s}\\{\text{Mesh 2: }}-V_{s}+R_{1}(I_{2}-I_{1})+{\frac {1}{sC}}(I_{2}-I_{3})=0\\{\text{Mesh 3: }}{\frac {1}{sC}}(I_{3}-I_{2})+R_{2}(I_{3}-I_{1})+sLI_{3}=0\\\end{cases}}\,$

После того как уравнения найдены, систему линейных уравнений можно решить, используя любой метод решения линейных уравнений .

Особые случаи

В токе сетки есть два особых случая: токи, содержащие суперсетку, и токи, содержащие зависимые источники .

Суперсетка

Суперсетка возникает, когда источник тока находится между двумя основными сетками. Сначала схема рассматривается так, как будто источника тока нет. Это приводит к одному уравнению, которое включает в себя два сетчатых тока. После того, как это уравнение сформировано, необходимо уравнение, которое связывает два тока сетки с источником тока . Это будет уравнение, в котором источник тока равен одному из токов сетки минус другой. Ниже приведен простой пример работы с суперсеткой. ^[2]

${\begin{cases}{\text{Mesh 1, 2: }}-V_{s}+R_{1}I_{1}+R_{2}I_{2}=0\\{\text{Current source: }}I_{s}=I_{2}-I_{1}\end{cases}}\,$

Зависимые источники

Зависимый источник — это источник тока или источник напряжения , который зависит от напряжения или тока другого элемента цепи. Когда зависимый источник содержится в основной сетке, к нему следует относиться как к независимому источнику. После формирования уравнения сетки необходимо уравнение зависимого источника. Это уравнение обычно называют уравнением связи. Это уравнение, которое связывает переменную зависимого источника с напряжением или током , от которого зависит источник в цепи. Ниже приведен простой пример зависимого источника. ^[2]

${\begin{cases}{\text{Mesh 1: }}-V_{s}+R_{1}I_{1}+R_{3}(I_{1}-I_{2})=0\\{\text{Mesh 2: }}R_{2}I_{2}+3I_{x}+R_{3}(I_{2}-I_{1})=0\\{\text{Dependent variable: }}I_{x}=I_{1}-I_{2}\end{cases}}\,$

См. также

Ссылки

^ Хейт, Уильям Х. и Кеммерли, Джек Э. (1993). Анализ инженерных цепей (5-е изд.), Нью-Йорк: McGraw Hill.
^ Jump up to: Перейти обратно: ^а ^б ^с ^д Нильссон, Джеймс В. и Ридель, Сьюзен А. (2002). Вводные схемы по электротехнике и вычислительной технике . Нью-Джерси: Прентис Холл.
^ Jump up to: Перейти обратно: ^а ^б ^с ^д Люг, Рассел Э. и Рейнхард, Эрвин А. (1972). Базовая электроника для инженеров и ученых (2-е изд.). Нью-Йорк: Международная компания по производству учебников.
^ Пакетт, Рассел Э. и Романовиц, Гарри А. (1976). Введение в электронику (2-е изд.). Сан-Франциско: John Wiley and Sons, Inc.

Внешние ссылки

[Hayt-1] Хейт, Уильям Х. и Кеммерли, Джек Э. (1993). Анализ инженерных цепей (5-е изд.), Нью-Йорк: McGraw Hill.

[Nilsson-2] Jump up to: Перейти обратно: ^а ^б ^с ^д Нильссон, Джеймс В. и Ридель, Сьюзен А. (2002). Вводные схемы по электротехнике и вычислительной технике . Нью-Джерси: Прентис Холл.

[Russell-3] Jump up to: Перейти обратно: ^а ^б ^с ^д Люг, Рассел Э. и Рейнхард, Эрвин А. (1972). Базовая электроника для инженеров и ученых (2-е изд.). Нью-Йорк: Международная компания по производству учебников.

[Romanowitz-4] Пакетт, Рассел Э. и Романовиц, Гарри А. (1976). Введение в электронику (2-е изд.). Сан-Франциско: John Wiley and Sons, Inc.

[1]

[2]

[3]

[4]