Инверсия (дискретная математика)

Перестановка с выделенной одной из ее инверсий. Инверсию можно обозначить парой позиций (2, 4) или парой элементов (5, 2). Инверсии этой перестановки с использованием обозначений на основе элементов: (3, 1), (3, 2), (5, 1), (5, 2) и (5,4).

В информатике и дискретной математике инверсией последовательности называется пара элементов , нарушающих свой естественный порядок .

Определения

Инверсия

Позволять $\pi$ быть перестановкой . имеет инверсия место $\pi$ между $i$ и $j$ если $i<j$ и $\pi (i)>\pi (j)$. Инверсия обозначается упорядоченной парой, содержащей либо места $(i,j)$ или элементы ${\bigl (}\pi (i),\pi (j){\bigr )}$.

Множество инверсий — это множество всех инверсий. Набор инверсий перестановки, использующий нотацию на основе места, такой же, как набор инверсий обратной перестановки, использующий нотацию на основе элементов, с заменой двух компонентов каждой упорядоченной пары. Аналогично, набор инверсий перестановки, использующий нотацию на основе элементов, такой же, как набор инверсий обратной перестановки, использующий нотацию на основе места, с заменой двух компонентов каждой упорядоченной пары.

Инверсии обычно определяются для перестановок, но также могут быть определены для последовательностей:
Позволять $S$ быть последовательностью (или мультимножественной перестановкой ). Если $i<j$ и $S(i)>S(j)$, либо пара мест $(i,j)$ или пара элементов ${\bigl (}S(i),S(j){\bigr )}$ называется инверсией $S$.

Для последовательностей инверсии согласно элементному определению не являются уникальными, поскольку разные пары мест могут иметь одну и ту же пару значений.

Номер инверсии

Число инверсии ${\mathtt {inv}}(X)$ последовательности $X=\langle x_{1},\dots ,x_{n}\rangle$, — мощность инверсионного множества. Это обычная мера сортировки (иногда называемая предварительной сортировкой) перестановки. или последовательность. Число инверсии находится между 0 и ${\frac {n(n-1)}{2}}$ включительно. Перестановка и обратная к ней имеют одинаковый номер инверсии.

Например ${\mathtt {inv}}(\langle 1,2,\dots ,n\rangle )=0$ поскольку последовательность упорядочена. Кроме того, когда $n=2m$ даже, ${\mathtt {inv}}(\langle m+1,m+2,\dots ,2m,1,2,\dots ,m\rangle )=m^{2}$ (поскольку каждая пара $(1\leq i\leq m<j\leq 2m)$ это инверсия). Этот последний пример показывает, что набор, который интуитивно «почти отсортирован», все же может иметь квадратичное количество инверсий.

Число инверсии — это количество пересечений на стрелочной диаграмме перестановки, перестановки тау-расстояние Кендалла от единичной перестановки и сумма каждого из векторов, связанных с инверсией, определенных ниже.

Другие меры сортировки включают минимальное количество элементов, которые можно удалить из последовательности, чтобы получить полностью отсортированную последовательность, количество и длину отсортированных «серий» внутри последовательности, правило Спирмена (сумма расстояний каждого элемента от его отсортированного элемента). позиция) и наименьшее количество обменов, необходимое для сортировки последовательности. Стандартные алгоритмы сортировки сравнением можно адаптировать для вычисления числа инверсий за время O( n log n ) .

Векторы, связанные с инверсией

Используются три похожих вектора, которые объединяют инверсии перестановки в вектор, однозначно определяющий ее. Их часто называют вектором инверсии или кодом Лемера . (Список источников находится здесь .)

В этой статье используется термин вектор инверсии ( $v$) как Вольфрам . Остальные два вектора иногда называют левым и правым вектором инверсии , но во избежание путаницы с вектором инверсии в этой статье они называются левым счетчиком инверсии ( $l$) и счетчик правой инверсии ( $r$). Интерпретируемый как факториал, счетчик левой инверсии дает перестановки, обратные колексикографическим, а правильный счетчик инверсий дает лексикографический индекс.

Диаграмма Роте

Вектор инверсии $v$:
С помощью на основе элементов определения $v(i)$ — количество инверсий, меньшая (правая) компонента которых равна $i$.

$v(i)$ это количество элементов в $\pi$ больше, чем $i$ до $i$.

$v(i)~~=~~\#\{k\mid k>i~\land ~\pi ^{-1}(k)<\pi ^{-1}(i)\}$

Левый счетчик инверсии $l$:
С места определением $l(i)$ — количество инверсий, больший (правый) компонент которых равен $i$.

$l(i)$ это количество элементов в $\pi$ больше, чем $\pi (i)$ до $\pi (i)$.

$l(i)~~=~~\#\left\{k\mid k<i~\land ~\pi (k)>\pi (i)\right\}$

Правильный счет инверсии $r$, часто называемый кодом Лемера :
С места определением $r(i)$ — количество инверсий, меньшая (левая) компонента которых равна $i$.

$r(i)$ это количество элементов в $\pi$ меньше, чем $\pi (i)$ после $\pi (i)$.

$r(i)~~=~~\#\{k\mid k>i~\land ~\pi (k)<\pi (i)\}$

Оба $v$ и $r$ можно найти с помощью диаграммы Роте , которая представляет собой матрицу перестановок с единицами, представленными точками, и инверсией (часто изображаемой крестом) в каждой позиции, где есть точка справа и под ней. $r(i)$ это сумма инверсий в строке $i$ диаграммы Роте, в то время как $v(i)$ представляет собой сумму инверсий в столбце $i$. Матрица перестановок обратного преобразования является транспонированной, поэтому $v$ перестановки $r$ обратного, и наоборот.

Пример: все перестановки четырех элементов.

Шесть возможных инверсий 4-элементной перестановки

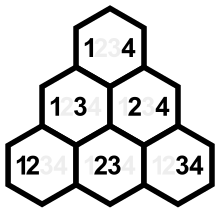
В следующей сортируемой таблице показаны 24 перестановки четырех элементов (в $\pi$ столбец) с их пространственными наборами инверсий (в столбце pb), векторами, связанными с инверсией (в столбце $v$, $l$, и $r$ столбцы) и числа инверсий (в столбце #). (Столбцы с мелким шрифтом и без заголовков являются отражением соседних с ними столбцов и могут использоваться для их сортировки в колексикографическом порядке .)

Видно, что $v$ и $l$ всегда иметь одни и те же цифры, и это $l$ и $r$ оба связаны с набором инверсий на основе места. Нетривиальные элементы $l$ представляют собой суммы нисходящих диагоналей изображенного треугольника и $r$ представляют собой суммы возрастающих диагоналей. (Пары в нисходящих диагоналях имеют общие правые компоненты 2, 3, 4, а пары в восходящих диагоналях имеют общие левые компоненты 1, 2, 3.)

Порядок таблицы по умолчанию — обратный порядок колексов по $\pi$, что аналогично упорядочиванию колексов по $l$. Лекс заказать по $\pi$ то же самое, что и порядок lex по $r$.

show3-элементные перестановки для сравнения
0 1 2 3 4 5 $\pi$ $v$ $l$ p-b $r$ # 0 123 321 000 000 000 000 000 000 0 1 213 312 100 001 010 010 100 001 1 2 132 231 010 010 100 001 010 010 1 3 312 213 110 011 110 011 200 002 2 4 231 132 200 002 200 002 110 011 2 5 321 123 210 012 210 012 210 012 3

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

$\pi$ $v$ $l$ пб $r$ # 0 1234 4321 000 0 0 000 000 0 0 000 000 0 0 000 0 1 2134 4312 100 0 0 001 001 0 0 100 100 0 0 001 1 2 1324 4231 010 0 0 010 010 0 0 010 010 0 0 010 1 3 3124 4213 110 0 0 011 011 0 0 110 200 0 0 002 2 4 2314 4132 200 0 0 002 020 0 0 020 110 0 0 011 2 5 3214 4123 210 0 0 012 021 0 0 120 210 0 0 012 3 6 1243 3421 001 0 0 100 100 0 0 001 001 0 0 100 1 7 2143 3412 101 0 0 101 101 0 0 101 101 0 0 101 2 8 1423 3241 011 0 0 110 110 0 0 011 020 0 0 020 2 9 4123 3214 111 0 0 111 111 0 0 111 300 0 0 003 3 10 2413 3142 201 0 0 102 120 0 0 021 120 0 0 021 3 11 4213 3124 211 0 0 112 121 0 0 121 310 0 0 013 4 12 1342 2431 020 0 0 020 200 0 0 002 011 0 0 110 2 13 3142 2413 120 0 0 021 201 0 0 102 201 0 0 102 3 14 1432 2341 021 0 0 120 210 0 0 012 021 0 0 120 3 15 4132 2314 121 0 0 121 211 0 0 112 301 0 0 103 4 16 3412 2143 220 0 0 022 220 0 0 022 220 0 0 022 4 17 4312 2134 221 0 0 122 221 0 0 122 320 0 0 023 5 18 2341 1432 300 0 0 003 300 0 0 003 111 0 0 111 3 19 3241 1423 310 0 0 013 301 0 0 103 211 0 0 112 4 20 2431 1342 301 0 0 103 310 0 0 013 121 0 0 121 4 21 4231 1324 311 0 0 113 311 0 0 113 311 0 0 113 5 22 3421 1243 320 0 0 023 320 0 0 023 221 0 0 122 5 23 4321 1234 321 0 0 123 321 0 0 123 321 0 0 123 6

Слабый порядок перестановок

Пермутоэдр симметрической группы S ₄

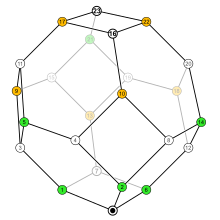
Множеству перестановок n элементов можно придать структуру частичного порядка , называемого слабым порядком перестановок , который образует решетку .

Диаграмма Хассе инверсионных множеств, упорядоченных подмножества , образует скелет пермутоэдра отношением .

Если каждому набору инверсий присваивается перестановка с использованием определения на основе места, результирующий порядок перестановок аналогичен пермутоэдру, где ребро соответствует замене двух элементов с последовательными значениями. Это слабый порядок перестановок. Тождество — это его минимум, а перестановка, образованная изменением тождества, — это его максимум.

Если бы каждому набору инверсий была назначена перестановка с использованием определения на основе элементов, результирующий порядок перестановок был бы таким же, как в графе Кэли , где ребро соответствует перестановке двух элементов в последовательных местах. Этот граф Кэли симметричной группы подобен ее пермутоэдру, но каждая перестановка заменена ее обратной.

См. также

• Факториальная система счисления
• Граф перестановок
• Транспозиции, простые транспозиции, инверсии и сортировка.
• Расстояние Дамерау – Левенштейна
• Четность перестановки

Последовательности в OEIS :

• Последовательности, связанные с представлением факторной базы
• Факториальные числа: A007623 и A108731.
• Номера инверсий: A034968
• Наборы инверсий конечных перестановок, интерпретируемых как двоичные числа: A211362 (связанная перестановка: A211363 )
• Конечные перестановки, в векторах инверсии которых есть только 0 и 1: A059590 (их наборы инверсий: A211364 ).
• Количество перестановок n элементов с k инверсиями; Числа Маона: A008302 (максимумы строк; числа Кендалла-Манна: A000140 )
• Количество связных помеченных графов с n ребрами и n узлами: A057500

Ссылки

Исходная библиография

• Айгнер, Мартин (2007). «Словопредставление». Курс счета . Берлин, Нью-Йорк: Springer. ISBN  978-3642072536 .
• Барт, Вильгельм; Мутцель, Петра (2004). «Простой и эффективный двухслойный перекрестный подсчет» . Журнал графовых алгоритмов и приложений . 8 (2): 179–194. дои : 10.7155/jgaa.00088 .
• Бона, Миклош (2012). «2.2 Инверсии в перестановках мультимножеств». Комбинаторика перестановок . Бока-Ратон, Флорида: CRC Press. ISBN  978-1439850510 .
• Конте, Луи (1974). «6.4 Инверсии перестановки [n]». Продвинутая комбинаторика; искусство конечных и бесконечных расширений . Дордрехт, Бостон: Паб D. Reidel. компании ISBN  9027704414 .
• Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2001). Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. ISBN  0-262-53196-8 .
• Гратцер, Джордж (2016). «7-2 Базовые объекты». Решетчатая теория. специальные темы и приложения . Хам, Швейцария: Биркхойзер. ISBN  978-3319442358 .
• Кляйнберг, Джон; Тардос, Ева (2005). Алгоритм проектирования . ISBN  0-321-29535-8 .
• Кнут, Дональд (1973). «5.1.1 Инверсии». Искусство компьютерного программирования . Паб Аддисон-Уэсли. компании ISBN  0201896850 .
• Махмуд, Хосам Махмуд (2000). «Сортировка неслучайных данных». Сортировка: теория распределения . Серия Wiley-Interscience по дискретной математике и оптимизации. Том. 54. Вили-IEEE. ISBN  978-0-471-32710-3 .
• Пеммараджу, Шрирам В.; Скиена, Стивен С. (2003). «Перестановки и комбинации». Вычислительная дискретная математика: комбинаторика и теория графов с Mathematica . Издательство Кембриджского университета. ISBN  978-0-521-80686-2 .
• Виттер, Дж.С.; Флажоле, доктор философии (1990). «Средний анализ алгоритмов и структур данных». Ин ван Леувен, Ян (ред.). Алгоритмы и сложность . Том. 1 (2-е изд.). Эльзевир. ISBN  978-0-444-88071-0 .

Дальнейшее чтение

• Марголиус, Барбара Х. (2001). «Перестановки с инверсиями». Журнал целочисленных последовательностей . 4 .

Меры предварительной сортировки

• Маннила, Хейкки (апрель 1985 г.). «Меры предварительной сортировки и оптимальные алгоритмы сортировки». Транзакции IEEE на компьютерах . С-34 (4): 318–325. дои : 10.1109/tc.1985.5009382 .
• Эстивилл-Кастро, Владимир; Вуд, Дерик (1989). «Новая мера предсортированности» . Информация и вычисления . 83 (1): 111–119. дои : 10.1016/0890-5401(89)90050-3 .
• Скиена, Стивен С. (1988). «Посягающие списки как мера предварительной сортировки». КУСОЧЕК . 28 (4): 755–784. дои : 10.1007/bf01954897 . S2CID   33967672 .