Расстроенный сюжет

Графики UpSet — это метод визуализации данных для отображения данных набора, содержащего более трех пересекающихся наборов . UpSet показывает пересечения в матрице, причем строки матрицы соответствуют наборам, а столбцы — пересечениям между этими наборами (или наоборот). Размер наборов и пересечений показаны в виде гистограмм .
История
[ редактировать ]Графики UpSet были впервые предложены в 2014 году. [ 1 ] Первый прототип был реализован как интерактивное веб-приложение. [ 2 ] Графики UpSet связаны с графиками мозаики , хотя графики мозаики предназначены для категориальных, а не заданных данных.
Графики UpSet стали популярными, когда они стали доступны в виде R -библиотеки на основе ggplot2 . [ 3 ] и впоследствии были перереализованы в различных языках программирования, таких как Python и других. [ 4 ] По состоянию на январь 2024 года UpSetR был загружен с CRAN более 1,5 миллиона раз, хотя последний раз обновлялся 5 лет назад. [ 5 ] Графики UpSet теперь часто используются вместо диаграмм Венна, особенно в науках о жизни. [ 6 ]
Использование
[ редактировать ]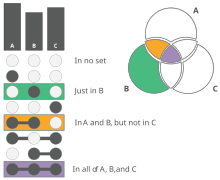

Графики UpSet визуализируют пересечения между наборами в матрице. На вертикальном графике UpSet столбцы матрицы соответствуют наборам, строки — пересечениям. Для каждой строки заполняются ячейки, являющиеся частью пересечения. Если заполнено несколько ячеек, они соединяются линией, чтобы подчеркнуть направление чтения графика. Поскольку наборы различаются по размеру, размер набора отображается в виде гистограммы поверх столбцов. Размер пересечений отображается в соответствии со строками, а также в виде гистограмм. Такая компоновка облегчает сравнение размеров отдельных пересечений, поскольку размеры стержней легко сравнивать. UpSets можно использовать горизонтально и вертикально.
Графики UpSet можно сортировать различными способами. Например, распространенный подход к сортировке — сортировка по мощности (размеру пересечения), при которой самые большие пересечения помещаются сверху. Альтернативная сортировка осуществляется по степени пересечения или по множествам.
Графики UpSet также можно использовать для визуализации атрибутов перекрестков, размещая визуализации атрибутов рядом со столбчатыми диаграммами. [ 7 ] Обычным выбором для этих визуализаций атрибутов являются подходы компактной визуализации для распределений, такие как коробчатые диаграммы или скрипичные диаграммы .
Расширенные функции графиков UpSet включают запрос, группировку и агрегирование данных. [ 1 ] Эти функции, как правило, доступны только в интерактивных веб-реализациях UpSet. [ 4 ]
Преимущества и ограничения
[ редактировать ]Графики UpSet, как правило, работают лучше, чем диаграммы Венна, для большего количества наборов и когда желательно также отображать контекстную информацию о пересечениях наборов. [ 8 ] Для визуализации диаграмм, содержащих менее трех наборов или когда пересечений всего несколько, обычно предпочтительнее использовать диаграммы Венна и Эйлера, поскольку они, как правило, более привычны и интуитивно понятны для чтения. [ 9 ]
Графики UpSet ограничены отображением 20-30 наборов, хотя специфика зависит от реальных данных. [ 9 ] Альтернативный подход для больших наборов данных — показать тепловую карту совместного появления , хотя они не могут отображать пересечения более высокого порядка. [ 9 ]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Jump up to: а б Лекс, Александр; Геленборг, Нильс; Стробельт, Хендрик; Вийемо, Ромен; Пфистер, Ханспетер (31 декабря 2014 г.). «UpSet: визуализация пересекающихся множеств» . Транзакции IEEE по визуализации и компьютерной графике . 20 (12): 1983–1992. дои : 10.1109/TVCG.2014.2346248 . ПМК 4720993 . ПМИД 26356912 .
- ^ Лекс, Александр; Геленборг, Нильс; Стробельт, Хендрик; Вийемо, Ромен; Пфистер, Ханспетер. " "UpSet — визуализация пересекающихся множеств" " .
- ^ Конвей, Джейк Р.; Лекс, Александр; Геленборг, Нильс (15 сентября 2017 г.). «UpSetR: пакет R для визуализации пересекающихся множеств и их свойств» . Биоинформатика . 33 (18): 2938–2940. doi : 10.1093/биоинформатика/btx364 . ПМК 5870712 . ПМИД 28645171 .
- ^ Jump up to: а б Лекс, Александр. "Расстройство" . расстроен.приложение . Проверено 18 февраля 2022 г.
- ^ Конвей, Джейк Р.; Геленборг, Нильс (9 мая 2019 г.). «УпсетР» . Гитхаб . Проверено 23 августа 2024 г.
- ^ Гадхаве, Киран. " "UpSet 2: от прототипа к инструменту" " . Проверено 28 апреля 2022 г.
- ^ Гу, Цзугуан. Расстроенный сюжет .
{{cite book}}:|website=игнорируется ( помогите ) - ^ Лора, Эллис. «Анализ множеств: сопоставление диаграмм Венна и графиков UpSet» . Маленькая мисс Дейта . Проверено 28 апреля 2022 г.
- ^ Jump up to: а б с Лекс, Александр; Геленборг, Нильс (1 августа 2014 г.). «Множества и пересечения» . Природные методы . 11 (8): 779. doi : 10.1038/nmeth.3033 . S2CID 39124565 .