Идеальная хэш-функция

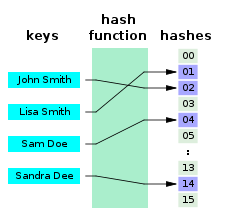
В информатике идеальная хэш-функция $h$ для набора $S$ — это хеш-функция , которая отображает различные элементы из $S$ в набор из $m$ целых чисел без каких-либо коллизий . С математической точки зрения это инъективная функция .

Совершенные хэш-функции могут использоваться для реализации справочной таблицы с постоянным временем доступа в худшем случае. Идеальная хеш-функция, как и любая хеш-функция , может использоваться для реализации хеш-таблиц с тем преимуществом, что не разрешение коллизий требуется реализовывать . Кроме того, если ключи отсутствуют в данных и известно, что запрошенные ключи будут действительными, то ключи не нужно хранить в таблице поиска, что позволяет сэкономить место.

Недостатки идеальных хеш-функций заключаются в том, что $S.$ для построения идеальной хэш-функции необходимо знать Нединамические идеальные хэш-функции необходимо перестроить, если $S$ изменится. Для часто меняющихся $S$ динамических совершенных хеш-функций можно использовать за счет дополнительного места. ^[1] Требуемое пространство для хранения идеальной хеш-функции находится в $O (n),$ где $n$ — количество ключей в структуре.

Важными параметрами производительности идеальных хеш-функций являются время вычисления, которое должно быть постоянным, время построения и размер представления.

Приложение

Идеальную хэш-функцию со значениями в ограниченном диапазоне можно использовать для эффективных операций поиска путем помещения ключей из $S$ (или других связанных значений) в таблицу поиска, индексируемую выходными данными функции. Затем можно проверить, присутствует ли ключ в $S$ , или найти значение, связанное с этим ключом, ища его в соответствующей ячейке таблицы. каждый такой поиск занимает постоянное время В худшем случае . ^[2] При идеальном хешировании связанные данные могут быть прочитаны или записаны с помощью одного доступа к таблице. ^[3]

Выполнение идеальных хэш-функций

Важными параметрами производительности для идеального хеширования являются размер представления, время оценки, время построения и, кроме того, требования к диапазону. ${\frac {m}{n}}$ (среднее количество сегментов на ключ в хеш-таблице). ^[4] Время оценки может достигать $O (1)$ , что является оптимальным. ^[2]^[4] Время построения должно быть не менее $O (n)$ , поскольку $каждый элемент в S$ необходимо учитывать $, а S$ содержит $n$ элементов. Эта нижняя граница может быть достигнута на практике. ^[4]

Нижняя граница размера представления зависит от $m$ и $n$ . Пусть $m = (1+ε) n$ и $h$ — идеальная хеш-функция. Хорошее приближение для нижней границы: $\log e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}$ Битов на элемент. Для минимального идеального хеширования $ε = 0$ нижняя граница равна $log e \approx 1,44$ бита на элемент. ^[4]

Строительство

Идеальная хеш-функция для конкретного набора $S$ , которую можно вычислить за постоянное время и со значениями в небольшом диапазоне, может быть найдена с помощью рандомизированного алгоритма за количество операций, пропорциональное размеру S.Исходная конструкция Фредмана, Комлоса и Семереди (1984) использует двухуровневую схему для сопоставления набора $S$ из $n$ элементов с диапазоном $индексов O (n)$ , а затем сопоставления каждого индекса с диапазоном значений хеш-функции. Первый уровень их построения выбирает большое простое число $p$ (больше, чем размер вселенной, из которой $нарисовано S$ ) и параметр $k$ , и сопоставляет каждый элемент $x$ из $S$ с индексом.

g(x)=(kx{\bmod {p}}){\bmod {n}}.

Если $k$ выбирается случайным образом, на этом этапе, вероятно, возникнут коллизии, но количество элементов $n i,$ одновременно отображаемых в один и тот же индекс $i,$ вероятно, будет небольшим.Второй уровень их построения задает непересекающиеся диапазоны $O (n i 2)$ целые числа для каждого индекса $i$ . Он использует второй набор линейных модульных функций, по одной для каждого индекса $i$ , чтобы отобразить каждый элемент $x$ из $S$ в диапазон, связанный с $g (x)$ . ^[2]

Как показывают Фредман, Комлос и Семереди (1984) , существует выбор параметра $k$ такой, что сумма длин диапазонов для $n$ различных значений $g (x)$ равна $O (n)$ . Кроме того, для каждого значения $g (x)$ существует линейная модульная функция, которая отображает соответствующее подмножество $S$ в диапазон, связанный с этим значением. И $k$ , и функции второго уровня для каждого значения $g (x)$ можно найти за полиномиальное время , выбирая значения случайным образом, пока не будет найден тот, который работает. ^[2]

Сама хеш-функция требует памяти $O (n)$ для хранения $k$ , $p$ и всех линейных модульных функций второго уровня. Вычисление хеш-значения данного ключа $x$ может выполняться за постоянное время путем вычисления $g (x)$ , поиска функции второго уровня, связанной с $g (x)$ , и применения этой функции к $x$ .Модифицированную версию этой двухуровневой схемы с большим количеством значений на верхнем уровне можно использовать для построения идеальной хеш-функции, которая отображает $S$ в меньший диапазон длины $n + o (n)$ . ^[2]

Более поздний метод построения идеальной хэш-функции описан Белаццуги, Ботельо и Дитцфельбингером (2009) как «хеширование, смещение и сжатие». хеш-функция первого уровня $g$ Здесь также используется $для сопоставления элементов с диапазоном из r$ целых чисел. Элемент $x \in S$ хранится в ведре $B g(x)$ . ^[4]

Затем, в порядке убывания размера, элементы каждого сегмента хешируются хеш-функцией последовательности независимых полностью случайных хеш-функций $(Φ 1, Φ 2, Φ 3, ...)$ , начиная с $Φ 1$ . Если хеш-функция не создает никаких коллизий для сегмента и результирующие значения еще не заняты другими элементами из других сегментов, функция выбирается для этого сегмента. Если нет, проверяется следующая хэш-функция в последовательности. ^[4]

Чтобы оценить идеальную хеш-функцию $h (x),$ нужно только сохранить отображение σ индекса сегмента $g (x)$ на правильную хеш-функцию в последовательности, в результате чего $h(x) = Φ σ(g(x))$ . ^[4]

Наконец, чтобы уменьшить размер представления, ( $σ(i)) 0 \leq i < r$ сжимаются в форму, которая по-прежнему позволяет выполнять оценку за $O (1)$ . ^[4]

Этот подход требует линейного времени по $n$ для построения и постоянного времени оценки. Размер представления находится в $O (n)$ и зависит от достигнутого диапазона. Например, при $m = 1,23 n$ Белаццуги, Ботельо и Дитцфельбингер (2009) достигли размера представления от 3,03 бит/ключ до 1,40 бит/ключ для приведенного примера набора из 10 миллионов записей, при этом более низкие значения требуют большего времени вычислений. Нижняя граница пространства в этом сценарии составляет 0,88 бит/ключ. ^[4]

Псевдокод

algorithm hash, displace, and compress is(1) Split S into buckets  $B i := g -1 ({i})\capS,0 \leq i < r$ (2) Sort buckets B_i in falling order according to size |B_i|(3) Initialize array T[0...m-1] with 0's(4) for all i ∈[r], in the order from (2), do(5)     for l ← 1,2,...(6)         repeat forming K_i ← { $Φ$ _l(x)|x ∈ B_i}(6)         until |K_i|=|B_i| and K_i∩{j|T[j]=1}= ∅(7)     let σ(i):= the successful l(8)     for all j ∈ K_i let T[j]:= 1(9) Transform (σ_i)_0≤i<r into compressed form, retaining  $O (1)$  access.

Нижние границы пространства

Использование $O (n)$ слов информации для хранения функции Фредмана, Комлоша и Семереди (1984) почти оптимально: любая идеальная хеш-функция, которую можно вычислить за постоянное время. пропорциональное размеру $S.$ требуется как минимум количество битов , ^[5]

Для минимальных совершенных хеш-функций нижняя граница теоретико-информационного пространства равна

\log _{2}e\approx 1.44

биты/ключ. ^[4]

Для идеальных хеш-функций сначала предполагается, что диапазон $h$ ограничен $n$ как $m = (1+ε) n$ . По формуле Белаццуги, Ботельо и Дитцфельбингера (2009) и для Вселенной $U\supseteq S$ чей размер $| У | = u$ стремится к бесконечности, нижняя граница пространства равна

\log _{2}e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}

бит/ключ, минус $log(n)$ бит в целом. ^[4]

Расширения

Идентификатор адреса памяти

Тривиальный, но распространенный пример идеального хеширования неявно присутствует в адресном пространстве (виртуальной) памяти компьютера. Поскольку каждый байт виртуальной памяти представляет собой отдельное, уникальное, напрямую адресуемое место хранения, значение начального адреса , по которому любой объект хранится в памяти, можно рассматривать как фактически идеальный хэш этого объекта во всем диапазоне адресов памяти. ^[6]

Динамическое идеальное хеширование

Использование идеальной хеш-функции лучше всего подходит в ситуациях, когда имеется часто запрашиваемый большой набор $S$ , который редко обновляется. Это связано с тем, что любая модификация набора $S$ может привести к тому, что хеш-функция перестанет быть идеальной для измененного набора. Решения, которые обновляют хэш-функцию каждый раз при изменении набора, известны как динамическое идеальное хеширование . ^[1] но эти методы относительно сложны в реализации.

Минимальная идеальная хэш-функция

Минимальная идеальная хэш-функция — это идеальная хеш-функция, которая сопоставляет $n$ ключей с $n$ последовательными целыми числами — обычно числами от $0$ до $n — 1$ или от $1$ до $n$ . Более формальный способ выразить это так: пусть $j$ и $k$ — элементы некоторого конечного $S.$ множества Тогда $h$ является минимальной совершенной хэш-функцией тогда и только тогда, когда $h (j) = h (k)$ влечет $j = k$ ( инъективность ) и существует целое число $a$ такое, что диапазон $h$ равен $a .. a + | С | - 1$ . Было доказано, что схема минимального идеального хеширования общего назначения требует как минимум $\log _{2}e\approx 1.44$ биты/ключ. ^[4] Предполагая, что $S$ это набор размеров $n$ содержащие целые числа в диапазоне $[1,2^{o(n)}]$ известно, как эффективно построить явную минимальную совершенную хеш-функцию из $S$ к $\{1,2,\ldots ,n\}$ который использует пространство $n\log _{2}e+o(n)$ бит и поддерживает постоянное время оценки. ^[7] На практике существуют минимально идеальные схемы хеширования, которые при наличии достаточного времени используют примерно 1,56 бита на ключ. ^[8]

k-идеальное хеширование

Хэш-функция является $k$ -идеальной, если не более $k$ элементов из $S$ сопоставляются с одним и тем же значением в диапазоне. Алгоритм «хеширования, смещения и сжатия» можно использовать для построения $k$ -совершенных хэш-функций, допуская до $k$ коллизий. Изменения, необходимые для этого, минимальны и подчеркнуты в адаптированном псевдокоде ниже:

(4) for all i ∈[r], in the order from (2), do(5)     for l ← 1,2,...(6)         repeat forming K_i ← { $Φ$ _l(x)|x ∈ B_i}(6)         until |K_i|=|B_i| and K_i∩{j|T[j]=k}= ∅(7)     let σ(i):= the successful l(8)     for all j ∈ K_i set T[j]←T[j]+1

Сохранение заказа

Минимальная совершенная хеш-функция $F$ сохраняет порядок, если ключи заданы в некотором порядке $1, a 2, ..., a n$ и для любых ключей $a j$ и $a k$ < $j a k$ подразумевает $F (a j) < F(а к)$ . ^[9] В этом случае значение функции — это просто позиция каждого ключа в отсортированном порядке всех ключей. Простая реализация сохраняющих порядок минимальных совершенных хэш-функций с постоянным временем доступа заключается в использовании (обычной) идеальной хеш-функции для хранения таблицы поиска позиций каждого ключа. В этом решении используется $O(n\log n)$ бит, что оптимально в ситуации, когда функция сравнения ключей может быть произвольной. ^[10] Однако если ключи $a 1, a 2, ..., a n$ являются целыми числами, взятыми из вселенной $\{1,2,\ldots ,U\}$ , то можно построить сохраняющую порядок хеш-функцию, используя только $O(n\log \log \log U)$ кусочки пространства. ^[11] Более того, эта оценка, как известно, оптимальна. ^[12]

Связанные конструкции

В то время как хеш-таблицы с хорошей размерностью имеют амортизированное среднее время O(1) (амортизированное среднее постоянное время) для поиска, вставки и удаления, большинство алгоритмов хеш-таблиц страдают от возможных наихудших случаев, которые занимают гораздо больше времени.Время O(1) в худшем случае (постоянное время даже в худшем случае) будет лучше для многих приложений (включая сетевой маршрутизатор и кэши памяти ). ^[13]^: 41

Лишь немногие алгоритмы хеш-таблиц поддерживают время поиска O(1) в наихудшем случае (постоянное время поиска даже в худшем случае). Те немногие, которые действительно включают: идеальное хеширование; динамическое идеальное хеширование ; кукушка хэширования ; классическое хеширование ; и расширяемое хеширование . ^[13]^: 42–69

Простая альтернатива идеальному хешированию, которая также допускает динамические обновления, — это хэширование с кукушкой . Эта схема сопоставляет ключи с двумя или более местоположениями в пределах диапазона (в отличие от идеального хеширования, которое сопоставляет каждый ключ с одним местоположением), но делает это таким образом, что ключи могут быть назначены один к одному местам, в которых они были. нанесено на карту. Поиск по этой схеме выполняется медленнее, поскольку необходимо проверять несколько местоположений, но, тем не менее, в худшем случае поиск занимает постоянное время. ^[14]

Ссылки

^ Jump up to: ^а ^б Дитцфельбингер, Мартин; Карлин, Анна ; Мельхорн, Курт ; Мейер ауф дер Хайде, Фридхельм; Ронерт, Ганс; Тарьян, Роберт Э. (1994), «Динамическое идеальное хеширование: верхняя и нижняя границы», SIAM Journal on Computing , 23 (4): 738–761, doi : 10.1137/S0097539791194094 , MR 1283572 .
^ Jump up to: ^а ^б ^с ^д ^и Фредман, Майкл Л .; Комлос, Янош ; Семереди, Эндре (1984), «Хранение разреженной таблицы с $временем доступа для наихудшего случая O (1)$ », Журнал ACM , 31 (3): 538, doi : 10.1145/828.1884 , MR 0819156 , S2CID 5399743
^ Лу, Йи ; Прабхакар, Баладжи ; Бономи, Флавио (2006), «Идеальное хеширование для сетевых приложений», Международный симпозиум IEEE по теории информации , 2006 г., стр. 2774–2778, doi : 10.1109/ISIT.2006.261567 , ISBN 1-4244-0505-Х , S2CID 1494710
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л Белазуги, Джамаль; Ботельо, Фабиано К.; Дитцфельбингер, Мартин (2009), «Хеширование, перемещение и сжатие» (PDF) , Алгоритмы - ESA 2009 (PDF) , Конспекты лекций по информатике , том. 5757, Берлин: Springer, стр. 682–693, CiteSeerX 10.1.1.568.130 , doi : 10.1007/978-3-642-04128-0_61 , ISBN 978-3-642-04127-3 , МР 2557794 .
^ Фредман, Майкл Л .; Комлос, Янош (1984), «О размере разделяющих систем и семейств совершенных хеш-функций», SIAM Journal on Algebraic and Discrete Methods , 5 (1): 61–68, doi : 10.1137/0605009 , MR 0731857 .
^ Витольд Литвин; Тадеуш Морзи; Готфрид Воссен (19 августа 1998 г.). Достижения в области баз данных и информационных систем . Springer Science+Business Media . п. 254. ИСБН 9783540649243 .
^ Хагеруп, Торбен; Толи, Торстен (2001), «Эффективное минимальное идеальное хеширование в почти минимальном пространстве» , STACS 2001 , Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 317–326, doi : 10.1007/3-540-44693-1_28 , ISBN 978-3-540-41695-1 , получено 12 ноября 2023 г.
^ Эспозито, Эммануэль; Мюллер Граф, Томас; Винья, Себастьяно (2020), «RecSplit: минимальное идеальное хеширование посредством рекурсивного разделения», 2020 г., Труды симпозиума по разработке алгоритмов и экспериментам (ALENEX) , Материалы , стр. 175–185, arXiv : 1910.06416 , doi : 10.1137/1.978161 1976007. 14 .
^ Дженкинс, Боб (14 апреля 2009 г.), «Минимально идеальное хеширование, сохраняющее порядок», в Блэке, Поле Э. (ред.), Словарь алгоритмов и структур данных , Национальный институт стандартов и технологий США , получено 5 марта 2013 г.
^ Фокс, Эдвард А.; Чен, Ци Фань; Дауд, Амджад М.; Хит, Ленвуд С. (июль 1991 г.), «Сохраняющие порядок минимальные совершенные хэш-функции и поиск информации» (PDF) , Транзакции ACM в информационных системах , 9 (3), Нью-Йорк, Нью-Йорк, США: ACM: 281–308, дои : 10.1145/125187.125200 , S2CID 53239140 .
^ Белазуги, Джамаль; Болди, Паоло; Паг, Расмус ; Винья, Себастьяно (ноябрь 2008 г.), «Теория и практика монотонного минимально совершенного хеширования», Журнал экспериментальной алгоритмики , 16 , ст. нет. 3.2, 26 стр., doi : 10.1145/1963190.2025378 , S2CID 2367401 .
^ Ассади, Сепер; Фарах-Колтон, Мартин; Кушмаул, Уильям (январь 2023 г.), «Жесткие границы для монотонного минимального идеального хеширования» , Труды ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA) 2023 г. , Филадельфия, Пенсильвания: Общество промышленной и прикладной математики, стр. 456–476 , arXiv : 2207.10556 , doi : 10.1137/1.9781611977554.ch20 , ISBN 978-1-61197-755-4 , получено 27 апреля 2023 г.
^ Jump up to: ^а ^б Тимоти А. Дэвис. «Глава 5 Хеширование» : подраздел «Хеш-таблицы с наихудшим доступом O(1)»
^ Паг, Расмус ; Родлер, Флемминг Фриш (2004), «Хеширование с кукушкой», Журнал алгоритмов , 51 (2): 122–144, doi : 10.1016/j.jalgor.2003.12.002 , MR 2050140 .

Дальнейшее чтение

Ричард Дж. Чичелли. Минимальные совершенные хеш-функции стали проще , Сообщения ACM, Vol. 23, номер 1, январь 1980 г.
Томас Х. Кормен , Чарльз Э. Лейзерсон , Рональд Л. Ривест и Клиффорд Стейн . Введение в алгоритмы , третье издание. МИТ Пресс, 2009. ISBN 978-0262033848 . Раздел 11.5: Идеальное хеширование, стр. 267, 277–282.
Фабиано К. Ботельо, Расмус Пах и Нивио Зивиани. «Бесшовное хеширование для приложений управления данными» .
Фабиано К. Ботельо и Нивио Зивиани . «Внешнее идеальное хеширование для очень больших наборов ключей» . 16-я конференция ACM по управлению информацией и знаниями (CIKM07), Лиссабон, Португалия, ноябрь 2007 г.
Джамаль Белаццуги, Паоло Больди, Расмус Пах и Себастьяно Винья. «Монотонное минимально идеальное хеширование: поиск в отсортированной таблице с доступом O (1)» . В материалах 20-го ежегодного симпозиума ACM-SIAM по дискретной математике (SODA), Нью-Йорк, 2009. ACM Press.
Маршалл Д. Брэйн и Алан Л. Тарп. «Почти идеальное хеширование больших наборов слов». Программное обеспечение – Практика и опыт, том. 19 (10), 967-078, октябрь 1989 г. Джон Уайли и сыновья.
Дуглас К. Шмидт, GPERF: идеальный генератор хеш-функций , отчет C++, SIGS, Vol. 10, № 10, ноябрь/декабрь 1998 г.

Внешние ссылки

gperf — идеальный генератор хэшей C и C++ с открытым исходным кодом (очень быстрый, но работает только для небольших наборов)
Минимальное идеальное хеширование (алгоритм Боба) Боба Дженкинса
cmph : C Minimal Perfect Hashing Library, реализации с открытым исходным кодом для многих (минимальных) идеальных хэшей (работает для больших наборов)
Sux4J : монотонное минимально идеальное хеширование с открытым исходным кодом на Java
MPHSharp : идеальные методы хеширования на C#
BBHash : минимальная идеальная хэш-функция в C++ только для заголовков.
Perfect::Hash — идеальный генератор хэшей на Perl, который создает код C. Имеет раздел «Предшествующий уровень техники», на который стоит обратить внимание.

[DynamicPerfectHashing-1] Jump up to: ^а ^б Дитцфельбингер, Мартин; Карлин, Анна ; Мельхорн, Курт ; Мейер ауф дер Хайде, Фридхельм; Ронерт, Ганс; Тарьян, Роберт Э. (1994), «Динамическое идеальное хеширование: верхняя и нижняя границы», SIAM Journal on Computing , 23 (4): 738–761, doi : 10.1137/S0097539791194094 , MR 1283572 .

[inventor-2] Jump up to: ^а ^б ^с ^д ^и Фредман, Майкл Л .; Комлос, Янош ; Семереди, Эндре (1984), «Хранение разреженной таблицы с $временем доступа для наихудшего случая O (1)$ », Журнал ACM , 31 (3): 538, doi : 10.1145/828.1884 , MR 0819156 , S2CID 5399743

[3] Лу, Йи ; Прабхакар, Баладжи ; Бономи, Флавио (2006), «Идеальное хеширование для сетевых приложений», Международный симпозиум IEEE по теории информации , 2006 г., стр. 2774–2778, doi : 10.1109/ISIT.2006.261567 , ISBN 1-4244-0505-Х , S2CID 1494710

[CHD-4] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л Белазуги, Джамаль; Ботельо, Фабиано К.; Дитцфельбингер, Мартин (2009), «Хеширование, перемещение и сжатие» (PDF) , Алгоритмы - ESA 2009 (PDF) , Конспекты лекций по информатике , том. 5757, Берлин: Springer, стр. 682–693, CiteSeerX 10.1.1.568.130 , doi : 10.1007/978-3-642-04128-0_61 , ISBN 978-3-642-04127-3 , МР 2557794 .

[5] Фредман, Майкл Л .; Комлос, Янош (1984), «О размере разделяющих систем и семейств совершенных хеш-функций», SIAM Journal on Algebraic and Discrete Methods , 5 (1): 61–68, doi : 10.1137/0605009 , MR 0731857 .

[6] Витольд Литвин; Тадеуш Морзи; Готфрид Воссен (19 августа 1998 г.). Достижения в области баз данных и информационных систем . Springer Science+Business Media . п. 254. ИСБН 9783540649243 .

[7] Хагеруп, Торбен; Толи, Торстен (2001), «Эффективное минимальное идеальное хеширование в почти минимальном пространстве» , STACS 2001 , Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 317–326, doi : 10.1007/3-540-44693-1_28 , ISBN 978-3-540-41695-1 , получено 12 ноября 2023 г.

[RecSplit-8] Эспозито, Эммануэль; Мюллер Граф, Томас; Винья, Себастьяно (2020), «RecSplit: минимальное идеальное хеширование посредством рекурсивного разделения», 2020 г., Труды симпозиума по разработке алгоритмов и экспериментам (ALENEX) , Материалы , стр. 175–185, arXiv : 1910.06416 , doi : 10.1137/1.978161 1976007. 14 .

[9] Дженкинс, Боб (14 апреля 2009 г.), «Минимально идеальное хеширование, сохраняющее порядок», в Блэке, Поле Э. (ред.), Словарь алгоритмов и структур данных , Национальный институт стандартов и технологий США , получено 5 марта 2013 г.

[10] Фокс, Эдвард А.; Чен, Ци Фань; Дауд, Амджад М.; Хит, Ленвуд С. (июль 1991 г.), «Сохраняющие порядок минимальные совершенные хэш-функции и поиск информации» (PDF) , Транзакции ACM в информационных системах , 9 (3), Нью-Йорк, Нью-Йорк, США: ACM: 281–308, дои : 10.1145/125187.125200 , S2CID 53239140 .

[11] Белазуги, Джамаль; Болди, Паоло; Паг, Расмус ; Винья, Себастьяно (ноябрь 2008 г.), «Теория и практика монотонного минимально совершенного хеширования», Журнал экспериментальной алгоритмики , 16 , ст. нет. 3.2, 26 стр., doi : 10.1145/1963190.2025378 , S2CID 2367401 .

[12] Ассади, Сепер; Фарах-Колтон, Мартин; Кушмаул, Уильям (январь 2023 г.), «Жесткие границы для монотонного минимального идеального хеширования» , Труды ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA) 2023 г. , Филадельфия, Пенсильвания: Общество промышленной и прикладной математики, стр. 456–476 , arXiv : 2207.10556 , doi : 10.1137/1.9781611977554.ch20 , ISBN 978-1-61197-755-4 , получено 27 апреля 2023 г.

[davis-13] Jump up to: ^а ^б Тимоти А. Дэвис. «Глава 5 Хеширование» : подраздел «Хеш-таблицы с наихудшим доступом O(1)»

[14] Паг, Расмус ; Родлер, Флемминг Фриш (2004), «Хеширование с кукушкой», Журнал алгоритмов , 51 (2): 122–144, doi : 10.1016/j.jalgor.2003.12.002 , MR 2050140 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]