Анализ разведения

Термин «анализ разбавления» обычно используется для обозначения особого типа биологического анализа , при котором один или несколько препаратов (например, лекарственное средство) вводятся в экспериментальные единицы при различных уровнях доз, вызывающих измеримый биологический ответ. Уровни доз получают путем разбавления разбавителем, который является инертным в отношении реакции. Экспериментальными единицами могут быть, например, клеточные культуры, ткани, органы или живые животные. Биологическая реакция может быть количественной (например, положительной/отрицательной) или количественной (например, рост). Цель состоит в том, чтобы связать реакцию с дозой, обычно с помощью методов интерполяции , и во многих случаях выразить эффективность/активность тестируемого препарата(ов) относительно стандарта известной эффективности/активности.

Анализы разведения могут быть прямыми и непрямыми. В анализе прямого разведения измеряется количество дозы, необходимое для получения специфического (фиксированного) ответа, так что доза является стохастической переменной, определяющей распределение толерантности . И наоборот, в анализе непрямого разведения уровни доз вводят при фиксированных уровнях дозы, так что ответ является стохастической переменной.

В некоторых анализах могут быть веские основания полагать, что все компоненты тестового препарата, кроме одного, не оказывают никакого влияния на изучаемую реакцию испытуемых. В этом случае анализ препарата на стандартный препарат эффективного компонента эквивалентен анализу для определения содержания компонента. Это можно назвать анализом аналитического разбавления .

Статистические модели

Для математического определения анализа разведения пространство наблюдения $U$ определена и функция $f:U\rightarrow \mathbb {R}$ так что ответы $u\in U$ отображаются в набор действительных чисел. Теперь предполагается, что функция $F$ существует, что связывает дозу $z\in [0,\infty )$ на ответ

f(u)=F(z)+e

в котором $e$ является ошибочным термином с ожиданием 0. $F$ обычно считается непрерывным и монотонным . Кроме того, в ситуациях, когда включен стандартный препарат, предполагается, что препарат для испытаний $T$ ведет себя как разбавление (или концентрация) стандарта $S$

F_{T}(z)=F_{S}(\rho z)

, для всех

z

где $\rho >0$ это относительная эффективность $T$ . Это фундаментальное предположение о сходстве кривых «доза-реакция», которое необходимо для значимого и однозначного определения относительной активности. Во многих случаях удобно применить степенное преобразование $x=z^{\lambda }$ с $\lambda >0$ или логарифмическое преобразование $x=\log(z)$ . Можно показать, что последнее является предельным случаем $\lambda \downarrow 0$ так что если $\lambda =0$ записано для логарифмического преобразования, приведенное выше уравнение можно переопределить как

F_{T}(x)=F_{S}(\rho ^{\lambda }x)

, для всех

x

.

Оценки ${\hat {F}}$ из $F$ обычно ограничиваются тем, что они являются членами четко определенного параметрического семейства функций , например семейства линейных функций, характеризующихся точкой пересечения и наклоном. Статистические методы, такие как оптимизация по максимальному правдоподобию, могут использоваться для расчета оценок параметров. Особое значение в этом отношении имеет теория обобщенных линейных моделей, с помощью которой можно моделировать широкий спектр анализов разбавления. Оценки $F$ может описать $F$ удовлетворительно в диапазоне испытанных доз, но они не обязательно должны описывать $F$ за пределами этого диапазона. Однако это не означает, что несходные кривые могут быть ограничены интервалом, где они оказываются похожими.

На практике, $F$ само по себе редко представляет интерес. Больший интерес представляет оценка $\rho$ или оценку дозы, вызывающей конкретный ответ. Эти оценки включают в себя взятие соотношений статистически зависимых оценок параметров. Теорему Филлера можно использовать для вычисления доверительных интервалов этих отношений.

Некоторые особые случаи заслуживают особого упоминания из-за их широкого использования: $F$ является линейным и $\lambda >0$ это известно как модель отношения наклона . Если $F$ является линейным и $\lambda =0$ это известно как модель параллельных линий . Другой широко применяемой моделью является пробит-модель , в которой $F$ — кумулятивная функция нормального распределения , $\lambda =0$ и $e$ следует биномиальному распределению .

Пример: Микробиологический анализ антибиотиков.

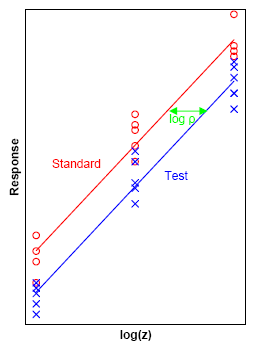
Стандарт антибиотика (показан красным) и тестируемый препарат (показан синим цветом) применяются в трех дозах к чувствительным микроорганизмам на слое агара в чашках Петри . Чем сильнее доза, тем больше зона подавления роста микроорганизмов. Биологический ответ $u$ в данном случае зона торможения и диаметр этой зоны $f(u)$ может быть использован в качестве измеримой реакции. Дозы $z$ преобразуются в логарифмы $x=\log(z)$ и метод наименьших квадратов используется для подгонки к данным двух параллельных линий. Горизонтальное расстояние $\log({\hat {\rho }})$ между двумя линиями (показаны зеленым) служит для оценки эффективности $\rho$ препарата для испытаний относительно стандарта.

Программное обеспечение

Основные пакеты статистического программного обеспечения не охватывают анализы разбавления, хотя у статистика не должно возникнуть трудностей с написанием подходящих сценариев или макросов для этой цели. Существует несколько пакетов программного обеспечения специального назначения для анализа разбавления.

Ссылки

Финни, диджей (1971). Пробит-анализ, 3-е изд. Издательство Кембриджского университета, Кембридж. ISBN 0-521-08041-X
Финни, диджей (1978). Статистический метод в биологических анализах, 3-е изд. Гриффин, Лондон. ISBN 0-02-844640-2
Говиндараджулу, З. (2001). Статистические методы биоанализа, 2-е исправленное и дополненное издание, Каргер, Нью-Йорк. ISBN 3-8055-7119-4

Внешние ссылки

Программное обеспечение для анализа разбавления: