Джонсон круги

В геометрии набор окружностей Джонсона трёх окружностей одинакового радиуса $r,$ имеющих одну общую точку пересечения $H.$ состоит из В такой конфигурации круги обычно имеют в общей сложности четыре пересечения (точки, где встречаются по крайней мере два из них): общая точка $H$ , которую они все разделяют, и для каждой из трех пар кругов еще одна точка пересечения (называемая здесь их двустороннее пересечение). Если какие-либо два круга соприкасаются, они имеют только $H$ в качестве общей точки, и тогда будет считаться, что $H$ также является их двусторонним пересечением; если они совпадают, мы объявляем их двустороннее пересечение точкой, диаметрально противоположной $H$ . Три точки пересечения по двум направлениям определяют опорный треугольник фигуры. Концепция названа в честь Роджера Артура Джонсона. ^{[ 1 ]}^{[ 2 ]}^{[ 3 ]}

Характеристики

Центры кругов Джонсона лежат на окружности того же радиуса $r,$ и круги Джонсона с центром в точке $H.$ что Эти центры образуют треугольник Джонсона .
Окружность с центром в точке $H$ и радиусом $2 r$ , известная как антидополнительная окружность, касается каждой из окружностей Джонсона. Три точки касания являются отражением точки $H$ относительно вершин треугольника Джонсона.
Точки касания кругов Джонсона и антидополнительного круга образуют еще один треугольник, называемый антидополнительным треугольником опорного треугольника. Он похож на треугольник Джонсона и гомотетичен в 2 раза с центром в $H$ , их общем центре описанной окружности.
Теорема Джонсона : точки двустороннего пересечения окружностей Джонсона (вершины опорного треугольника $△ ABC$ ) лежат на окружности того же радиуса $r$ , что и окружности Джонсона. Это свойство также хорошо известно в Румынии как проблема монеты в 5 леев Георгия Цитейки .
Отсчетный треугольник фактически конгруэнтен треугольнику Джонсона и гомотетичен ему в -1 раз.
Точка $H$ является ортоцентром опорного треугольника и центром описанной окружности треугольника Джонсона.
Гомотетичным центром треугольника Джонсона и опорного треугольника является их общий девятиточечный центр .

Доказательства

Свойство 1 очевидно из определения. Свойство 2 также ясно: для любой окружности радиуса $r$ и любой точки $P$ на ней окружность радиуса $2 r$ с центром в $P$ касается окружности в своей точке, противоположной $P$ ; в частности, к $P = H$ , давая антидополнительную окружность $C.$ это относится , Отсюда сразу следует свойство 3 в формулировке гомотетии; треугольник точек касания известен как антидополнительный треугольник.

Для свойств 4 и 5 сначала заметим, что любые два из трех кругов Джонсона меняются местами при отражении в прямой, соединяющей $H$ и их 2-кратное пересечение (или в их общей касательной в $H,$ если эти точки должны совпадать), и это отражение также меняет местами две вершины антидополнительного треугольника, лежащие на этих окружностях. Таким образом, точка двустороннего пересечения является серединой стороны антидополнительного треугольника, а $H$ лежит на серединном перпендикуляре этой стороны. Теперь середины сторон любого треугольника являются изображениями его вершин по гомотетии с коэффициентом -½ с центром в барицентре треугольника. Применительно к антидополнительному треугольнику, который сам получается из треугольника Джонсона посредством гомотетии с коэффициентом 2, из композиции гомотетий следует, что опорный треугольник гомотетичен треугольнику Джонсона с коэффициентом -1. Поскольку такая гомотетия является конгруэнцией , это дает свойство 5, а также теорему Джонсона об окружностях, поскольку конгруэнтные треугольники имеют описанные круги одинакового радиуса.

Для свойства 6 уже установлено, что все серединные перпендикуляры сторон антидополнительного треугольника проходят через точку $H$ ; поскольку эта сторона параллельна стороне опорного треугольника, эти серединные перпендикуляры также являются высотами опорного треугольника.

Свойство 7 непосредственно следует из свойства 6, поскольку гомотетический центр с коэффициентом -1 должен лежать в середине центров описанных окружностей $O$ опорного треугольника и $H$ треугольника Джонсона; последний является ортоцентром опорного треугольника, а его центр из девяти точек, как известно, является этой средней точкой. Поскольку центральная симметрия также отображает ортоцентр опорного треугольника в ортоцентр треугольника Джонсона, гомотетический центр также является девятиточечным центром треугольника Джонсона.

Существует также алгебраическое доказательство теоремы Джонсона об окружностях с использованием простого векторного вычисления. Есть векторы ${\vec {u}},{\vec {v}},{\vec {w}},$ все длины $r$ , такие, что круги Джонсона центрированы соответственно в $H+{\vec {u}},H+{\vec {v}},H+{\vec {w}}.$ Тогда точки двустороннего пересечения соответственно равны $H+{\vec {u}}+{\vec {v}},H+{\vec {u}}+{\vec {w}},H+{\vec {v}}+{\vec {w}}$ , и точка $H+{\vec {u}}+{\vec {v}}+{\vec {w}}$ очевидно, имеет расстояние $r$ до любой из этих точек двустороннего пересечения.

Дополнительные свойства

Три круга Джонсона можно рассматривать как отражения описанной окружности опорного треугольника относительно каждой из трех сторон опорного треугольника. Кроме того, при размышлениях о трех сторонах опорного треугольника его ортоцентр $H$ отображается в три точки на описанной окружности опорного треугольника, которые образуют вершины описанного ортогонального треугольника , а его центр описанной окружности $O$ отображается на вершины треугольника Джонсона. а его линия Эйлера (линия, проходящая через $O, N, H$ ) порождает три линии, совпадающие в точке X (110).

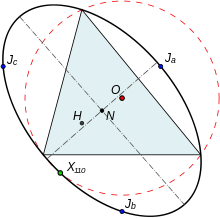
Треугольник Джонсона и его опорный треугольник имеют один и тот же центр из девяти точек, одну и ту же линию Эйлера и одну и ту же окружность из девяти точек . Все шесть точек, образованных из вершин опорного треугольника и его треугольника Джонсона, лежат на описанной окружности Джонсона , центр которой находится в центре девяти точек и имеет точку X (216) опорного треугольника в качестве своей перспективы. Описанная окружность и описанная окружность имеют общую четвертую точку X (110) опорного треугольника.

Наконец, есть две интересные и документированные описанные окружности, которые проходят через шесть вершин опорного треугольника и его треугольника Джонсона, а также центр описанной окружности, ортоцентр и девятиточечный центр. Первый известен как первый куб Массельмана – К 026. Этот куб также проходит через шесть вершин медиального треугольника и медиальный треугольник треугольника Джонсона. Вторая кубика известна как центральная кубика Эйлера – K 044. Эта кубика также проходит через шесть вершин ортогонального треугольника и ортогонального треугольника треугольника Джонсона.

Обозначение точки X ( i Кларка Кимберлинга ETC. ) представляет собой классификацию центров треугольников

Внешние ссылки

Вайсштейн, Эрик В. «Теорема Джонсона» . Математический мир .
ФМ Джексон и Вайсштейн, Эрик В. «Круги Джонсона» . Математический мир .
ФМ Джексон и Вайсштейн, Эрик В. «Треугольник Джонсона» . Математический мир .
Вайсштейн, Эрик В. «Джонсон Циркумконик» . Математический мир .
Вайсштейн, Эрик В. «Антикомплементарный треугольник» . Математический мир .
Вайсштейн, Эрик В. «Окружно-ортический треугольник» . Математический мир .
Бернар Гиберт Циркумкубический K026
Бернар Гиберт Циркумкуб K044
Кларк Кимберлинг, « Энциклопедия центров треугольника ». (Перечисляет около 3000 интересных точек, связанных с любым треугольником.)

Ссылки

^ Роджер Артур Джонсон, Современная геометрия : Элементарный трактат о геометрии треугольника и круга , Хоутон, компания Mifflin, 1929 г.
^ Роджер Артур Джонсон, «Теорема о круге», American Mathematical Monthly 23, 161–162, 1916.
^ Роджер Артур Джонсон (1890–1954). Архивировано 13 сентября 2014 г. в Wayback Machine.

[1] Роджер Артур Джонсон, Современная геометрия : Элементарный трактат о геометрии треугольника и круга , Хоутон, компания Mifflin, 1929 г.

[2] Роджер Артур Джонсон, «Теорема о круге», American Mathematical Monthly 23, 161–162, 1916.

[3] Роджер Артур Джонсон (1890–1954). Архивировано 13 сентября 2014 г. в Wayback Machine.

[ 1 ]

[ 2 ]

[ 3 ]