Недетерминированный конечный автомат

DFA для этого языка имеет как минимум 16 состояний.
В теории автоматов называется конечный автомат детерминированным конечным автоматом (ДКА), если
- каждый из его переходов однозначно определяется его исходным состоянием и входным символом, и
- чтение входного символа требуется для каждого перехода состояний.
Недетерминированный конечный автомат ( NFA ) или недетерминированный конечный автомат не обязан подчиняться этим ограничениям. В частности, каждый DFA также является NFA. Иногда термин NFA используется в более узком смысле, имея в виду NFA, который не является DFA, но не в этой статье.
Используя алгоритм построения подмножества , каждый NFA можно преобразовать в эквивалентный DFA; т. е. DFA, распознающий тот же формальный язык . [ 1 ] Как и DFA, NFA распознают только обычные языки .
НФА были представлены в 1959 году Майклом О. Рабином и Даной Скотт . [ 2 ] которые также показали свою эквивалентность DFA. NFA используются при реализации регулярных выражений : конструкция Томпсона представляет собой алгоритм компиляции регулярного выражения в NFA, который может эффективно выполнять сопоставление с образцом в строках. И наоборот, алгоритм Клини можно использовать для преобразования NFA в регулярное выражение (размер которого обычно экспоненциален во входном автомате).
NFA были обобщены несколькими способами, например, недетерминированные конечные автоматы с ε-ходами , преобразователи с конечным состоянием , автоматы с выталкиванием , альтернативные автоматы , ω-автоматы и вероятностные автоматы . Помимо DFA, существуют и другие известные частные случаи NFA. являются однозначными конечными автоматами (UFA) и самопроверяющиеся конечные автоматы (SVFA).
Неофициальное знакомство
[ редактировать ]Есть два способа описать поведение NFA, и оба они эквивалентны. Первый способ использует недетерминизм в названии NFA. Для каждого входного символа NFA переходит в новое состояние до тех пор, пока все входные символы не будут использованы. На каждом шаге автомат недетерминированно «выбирает» один из подходящих переходов. Если существует хотя бы один «счастливый ход», то есть некоторая последовательность выборов, ведущая к состоянию принятия после полного использования входных данных, он принимается. В противном случае, т.е. если никакая последовательность выбора вообще не может использовать весь входной сигнал [ 3 ] и приводят к состоянию принятия, ввод отклоняется. [ 4 ] : 19 [ 5 ] : 319
Во втором случае NFA принимает строку входных символов один за другим. На каждом этапе, когда применимы два или более перехода, он «клонирует» себя в соответствующее количество копий, каждая из которых следует за другим переходом. Если переход не применим, текущая копия находится в тупике и «умирает». Если после использования всех входных данных какая-либо из копий находится в состоянии принятия, входные данные принимаются, в противном случае они отклоняются. [ 4 ] : 19–20 [ 6 ] : 48 [ 7 ] : 56
Формальное определение
[ редактировать ]Более элементарное введение формального определения см. в теории автоматов .
Автомат
[ редактировать ]NFA кортежем формально представлен из 5 , состоящий из
- конечное множество состояний ,
- конечный набор входных символов ,
- функция перехода : ,
- начальное стартовое (или ) состояние , и
- набор состояний различаются как принимающие (или конечные ) состояния .
Здесь, обозначает мощности набор .
Признанный язык
[ редактировать ]Учитывая НФА , его признанный язык обозначается и определяется как набор всех строк в алфавите которые принимаются .
В соответствии с приведенными выше неформальными объяснениями существует несколько эквивалентных формальных определений строки. быть принятым :
- принимается, если последовательность состояний, , существует в такой, что:
- , для
- .
- На словах первое условие говорит о том, что машина запускается в стартовом состоянии. . Второе условие гласит, что для каждого символа строки , машина будет переходить из состояния в состояние в соответствии с функцией перехода. . Последнее условие говорит о том, что машина принимает если последний ввод приводит к остановке машины в одном из принимающих состояний. Для того, чтобы быть принятым , не требуется, чтобы каждая последовательность состояний заканчивалась состоянием принятия, достаточно, если это так. В противном случае, т.е. если вообще невозможно получить из в состояние из следуя , говорят, что автомат отвергает строку. Набор струн принимает язык признанный , и этот язык обозначается . [ 5 ] : 320 [ 6 ] : 54
- Альтернативно, принимается, если , где определяется рекурсивно :
- где пустая строка, и
- для всех .
- Другими словами, это набор всех состояний, достижимых из состояния потребляя строку . Строка принимается, если какое-то принимающее состояние в может быть достигнуто из начального состояния потребляя . [ 4 ] : 21 [ 7 ] : 59
Исходное состояние
[ редактировать ]Приведенное выше определение автомата использует одно начальное состояние , в котором нет необходимости. Иногда NFA определяются набором начальных состояний. Существует простая конструкция, которая переводит НКА с несколькими начальными состояниями в НКА с одним начальным состоянием, что обеспечивает удобную систему обозначений.
Пример
[ редактировать ] |
 |
 Метка дуги: входной символ, метка узла : состояние, зеленый : начальное состояние, красный : принимающее состояние(я). | |
Следующий автомат , с двоичным алфавитом, определяет, заканчивается ли вход на 1. Позволять где функция перехода может быть определен с помощью этой таблицы переходов состояний (см. верхний левый рисунок):
- ВходСостояние
0 1
С момента набора содержит более одного состояния, является недетерминированным.
Язык может быть описан обычным языком, заданным регулярным выражением (0|1)*1.
Все возможные последовательности состояний для входной строки «1011» показаны на нижнем рисунке. Строка принимается поскольку одна последовательность состояний удовлетворяет приведенному выше определению; не имеет значения, что другие последовательности этого не делают. Картину можно интерпретировать двояко:
- С точки зрения приведенного выше объяснения «счастливого пути», каждый путь на картинке обозначает последовательность вариантов выбора. .
- Что касается объяснения «клонирования», в каждом вертикальном столбце показаны все клоны в данный момент времени множественные стрелки, исходящие из узла, указывают на клонирование, узел без исходящих стрелок указывает на «смерть» клона.
Возможность прочтения одной и той же картинки двумя способами также указывает на эквивалентность обоих приведенных выше объяснений.
- Учитывая первое из приведенных выше формальных определений, «1011» принимается, так как при его чтении может пересекать последовательность состояний , удовлетворяющий условиям 1–3.
- Что касается второго формального определения, вычисления снизу вверх показывают, что , следовательно , следовательно , следовательно , и, следовательно, ; поскольку это множество не не пересекается с , строка «1011» принимается.
Напротив, строка «10» отклоняется (все возможные последовательности состояний для этого входа показаны на верхнем правом рисунке), поскольку невозможно достичь единственного принимающего состояния, , прочитав последний символ 0. Пока может быть достигнуто после потребления начальной «1», это не означает, что ввод «10» принят; скорее, это означает, что будет принята входная строка «1».
Эквивалентность DFA
[ редактировать ]Детерминированный конечный автомат (DFA) можно рассматривать как особый вид NFA, в котором для каждого состояния и символа функция перехода имеет ровно одно состояние. Таким образом, ясно, что любой формальный язык , который может быть распознан DFA, может быть распознан и NFA.
И наоборот, для каждого NFA существует DFA, распознающий один и тот же формальный язык. DFA может быть построен с использованием конструкции powerset .
Этот результат показывает, что NFA, несмотря на свою дополнительную гибкость, не способны распознавать языки, которые не могут быть распознаны некоторыми DFA. На практике это также важно для преобразования более простых в построении NFA в более эффективно исполняемые DFA. Однако, если NFA имеет n состояний, результирующий DFA может иметь до 2 состояний. н штатов, что иногда делает строительство нецелесообразным для крупных НФА.
NFA с ε-ходами
[ редактировать ]Недетерминированный конечный автомат с ε-ходами (NFA-ε) является дальнейшим обобщением NFA. В автомате такого типа функция перехода дополнительно определяется на пустой строке ε. Переход без использования входного символа называется ε-переходом и обозначается на диаграммах состояний стрелкой с надписью «ε». ε-переходы обеспечивают удобный способ моделирования систем, текущие состояния которых точно не известны: т. е., если мы моделируем систему и неясно, должно ли текущее состояние (после обработки некоторой входной строки) быть q или q', тогда мы можем добавить ε-переход между этими двумя состояниями, тем самым переводя автомат в оба состояния одновременно.
Формальное определение
[ редактировать ]NFA -ε формально представляется кортежем из пяти чисел : , состоящий из
- конечное множество состояний
- конечный набор входных символов, называемый алфавитом
- перехода функция
- начальное стартовое (или ) состояние
- набор состояний различаются как принимающие (или конечные ) состояния .
Здесь, обозначает мощности набор и обозначает пустую строку.
ε-замыкание состояния или набора состояний
[ редактировать ]Для государства , позволять обозначают множество состояний, достижимых из следуя ε-переходам в переходной функции , то есть, если существует последовательность состояний такой, что
- ,
- для каждого , и
- .
известно как эпсилон-замыкание (также ε-замыкание ) .
ε-замыкание множества состояний NFA определяется как набор состояний, достижимых из любого состояния в после ε-переходов. Формально для , определять .
Расширенная функция перехода
[ редактировать ]Подобно NFA без ε-ходов, функция перехода NFA-ε можно расширить до строк. Неофициально, обозначает набор всех состояний, которых мог достичь автомат при запуске в состоянии и читаем строку Функция можно определить рекурсивно следующим образом.
- , для каждого штата и где обозначает эпсилон-замыкание;
- Неформально: чтение пустой строки может вывести автомат из состояния. к любому состоянию эпсилон-замыкания
- для каждого штата каждая строка и каждый символ
- Неофициально: чтение строки может вывести автомат из состояния в любое государство в рекурсивно вычисленном наборе ; после этого, читая символ может отогнать его от в любое состояние в эпсилон-замыкании
Говорят, что автомат принимает строку если
то есть если читать может вывести автомат из стартового состояния в какое-то принимающее государство в [ 4 ] : 25
Пример
[ редактировать ]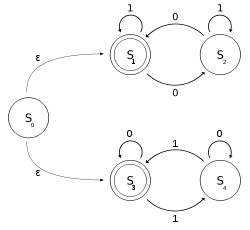
Позволять быть NFA-ε с двоичным алфавитом, который определяет, содержит ли вход четное количество нулей или четное количество единиц. Обратите внимание, что 0 вхождений также является четным числом вхождений.
В формальных обозначениях пусть где отношение перехода может быть определен этой таблицей перехода состояний :
Вход Состояние
|
0 | 1 | е |
|---|---|---|---|
| С 0 | {} | {} | { С 1 , С 3 } |
| С 1 | { С 2 } | { С 1 } | {} |
| SS2 | { С 1 } | { С 2 } | {} |
| С 3 | { С 3 } | { С 4 } | {} |
| С 4 | { С 4 } | { С 3 } | {} |
можно рассматривать как объединение двух DFA : одного с государствами а другой с состояниями . Язык может быть описан обычным языком, заданным этим регулярным выражением . Мы определяем используя ε-ходы, но можно определить без использования ε-ходов.
Эквивалент NFA
[ редактировать ]Чтобы показать, что NFA-ε эквивалентен NFA, сначала заметим, что NFA является частным случаем NFA-ε, поэтому осталось показать, что для каждого NFA-ε существует эквивалентный NFA.
Учитывая NFA с эпсилон-ходами определить NFA где
и
- для каждого штата и каждый символ используя расширенную функцию перехода определено выше.
Следует различать переходные функции и а именно и и их расширения до строк, и соответственно. По конструкции, не имеет электронных переходов.
Можно доказать, что для каждой строки , индукцией по длине
На основании этого можно показать, что тогда и только тогда, когда для каждой строки
- Если это следует из определения
- В противном случае, пусть с и
- От и у нас есть нам еще предстоит показать " " направление.
- Если содержит состояние в затем содержит одно и то же состояние, которое лежит в .
- Если содержит и затем также содержит состояние в а именно
- Если содержит и но тогда существует состояние в , и это же состояние должно находиться в [ 4 ] : 26–27
Поскольку NFA эквивалентен DFA, NFA-ε также эквивалентен DFA.
Свойства замыкания
[ редактировать ]
Набор языков, распознаваемых НФА, замыкается при следующих операциях. Эти операции замыкания используются в алгоритме построения Томпсона , который конструирует NFA из любого регулярного выражения . Их также можно использовать для доказательства того, что NFA распознают именно обычные языки .
- Союз (ср. картинку); то есть, если язык L 1 принимается некоторым НКА А 1 и L 2 некоторым А 2 , то можно построить НКА А u , который принимает язык L 1 ∪ L 2 .
- Пересечение; аналогично, из A 1 и A 2 НКА A i, можно построить допускающую L 1 ∩ L 2 .
- Конкатенация
- Отрицание; аналогично, из A 1 НКА An , который принимает Σ можно построить * \ Л 1 .
- Закрытие Клини
Поскольку НКА эквивалентны недетерминированному конечному автомату с ε-ходами (НКА-ε), указанные выше замыкания доказываются с использованием свойств замыкания НКА-ε.
Характеристики
[ редактировать ]Машина запускается в указанном начальном состоянии и считывает строку символов из своего алфавита . Автомат использует функцию перехода состояний Δ для определения следующего состояния, используя текущее состояние и только что прочитанный символ или пустую строку. Однако «следующее состояние NFA зависит не только от текущего события ввода, но и от произвольного количества последующих событий ввода. Пока эти последующие события не произойдут, невозможно определить, в каком состоянии находится машина». [ 8 ] Если, когда автомат завершил чтение, он находится в состоянии принятия, говорят, что NFA принимает строку, в противном случае говорят, что он отклоняет строку.
Набор всех строк, принимаемых NFA, — это язык, который принимает NFA. Этот язык является обычным языком .
Для каждого NFA детерминированный конечный автомат можно найти (DFA), который принимает тот же язык. Следовательно, можно преобразовать существующий NFA в DFA с целью реализации (возможно) более простой машины. Это можно выполнить с помощью конструкции powerset , которая может привести к экспоненциальному росту количества необходимых состояний. Формальное доказательство конструкции Powerset можно найти в статье о конструкции Powerset .
Выполнение
[ редактировать ]Существует множество способов реализации NFA:
- Преобразование в эквивалентный DFA. В некоторых случаях это может привести к экспоненциальному увеличению числа состояний. [ 9 ]
- Сохраняйте заданную структуру данных всех состояний, в которых в данный момент может находиться NFA. При потреблении входного символа объединяйте результаты функции перехода, примененной ко всем текущим состояниям, чтобы получить набор следующих состояний; если ε-ходы разрешены, включить все состояния, достижимые таким ходом (ε-замыкание). Каждый шаг требует не более s 2 вычислений, где s — количество состояний НКА. При потреблении последнего входного символа, если одно из текущих состояний является конечным, машина принимает строку. Строка длины n может быть обработана за время O ( ns 2 ), [ 7 ] : 153 и пространство O ( s ).
- Создайте несколько копий. Для каждого n- путевого решения NFA создает до n -1 копий машины. Каждый войдет в отдельное состояние. Если после использования последнего входного символа хотя бы одна копия NFA находится в состоянии принятия, NFA примет. (Это также требует линейного хранения по отношению к количеству состояний NFA, поскольку для каждого состояния NFA может быть одна машина.)
- Явно распространяйте токены через структуру перехода NFA и сопоставляйте их всякий раз, когда токен достигает конечного состояния. Иногда это полезно, когда NFA должен закодировать дополнительный контекст событий, вызвавших переход. (Для реализации, использующей этот метод для отслеживания ссылок на объекты, посмотрите Tracematches.) [ 10 ]
Сложность
[ редактировать ]- Можно за линейное время решить проблему пустоты для NFA, т. е. проверить, пуст ли язык данного NFA. Для этого мы можем просто выполнить поиск в глубину из начального состояния и проверить, можно ли достичь какого-то конечного состояния.
- PSPACE - полная проверка данного NFA, является ли он универсальным , т. е. существует ли строка, которую он не принимает. [ 11 ] Как следствие, то же самое верно и для проблемы включения , т. е. для двух NFA язык одного является подмножеством языка другого.
- Учитывая, что на входе NFA A и целое число n, проблема подсчета определения того, сколько слов длины n принимается A , является неразрешимой; это #P -сложно . Фактически, эта проблема является полной (при экономных редукциях ) для класса сложности SpanL . [ 12 ]
Применение НФА
[ редактировать ]NFA и DFA эквивалентны в том смысле, что если язык распознается NFA, он также распознается DFA и наоборот. Установление такой эквивалентности важно и полезно. Это полезно, потому что построить NFA для распознавания данного языка иногда намного проще, чем построить DFA для этого языка. Это важно, поскольку NFA можно использовать для уменьшения сложности математической работы, необходимой для установления многих важных свойств в теории вычислений . Например, гораздо проще доказать свойства замыкания регулярных языков, используя NFA, чем DFA.
См. также
[ редактировать ]- Детерминированный конечный автомат
- Двусторонний недетерминированный конечный автомат
- Нажимной автомат
- Недетерминированная машина Тьюринга
Примечания
[ редактировать ]- ^ Мартин, Джон (2010). Введение в языки и теорию вычислений . МакГроу Хилл. п. 108. ИСБН 978-0071289429 .
- ^ Рабин, Миссури; Скотт, Д. (апрель 1959 г.). «Конечные автоматы и проблемы их решения». Журнал исследований и разработок IBM . 3 (2): 114–125. дои : 10.1147/рд.32.0114 .
- ^ Последовательность выбора может привести к «тупику», когда переход для текущего входного символа неприменим; в этом случае оно считается неудачным.
- ^ Jump up to: а б с д и Джон Э. Хопкрофт и Джеффри Д. Ульман (1979). Введение в теорию автоматов, языки и вычисления . Ридинг/Массачусетс: Аддисон-Уэсли. ISBN 0-201-02988-Х .
- ^ Jump up to: а б Альфред В. Ахо, Джон Э. Хопкрофт и Джеффри Д. Ульман (1974). Проектирование и анализ компьютерных алгоритмов . Ридинг/Массачусетс: Аддисон-Уэсли. ISBN 0-201-00029-6 .
- ^ Jump up to: а б Майкл Сипсер (1997). Введение в теорию вычислений . Бостон/Массачусетс: ISBN издательства PWS Publishing Co. 0-534-94728-Х .
- ^ Jump up to: а б с Джон Э. Хопкрофт, Раджив Мотвани и Джеффри Д. Уллман (2003). Введение в теорию автоматов, языки и вычисления (PDF) . Река Аппер-Сэддл/Нью-Джерси: Эддисон Уэсли. ISBN 0-201-44124-1 .
- ^ FOLDOC Бесплатный онлайн-словарь по вычислительной технике, конечным автоматам
- ^ Крис Калабро (27 февраля 2005 г.). «Разрушение NFA и DFA» (PDF) . cseweb.ucsd.edu . Проверено 6 марта 2023 г.
- ^ Аллан К., Августинов П., Кристенсен А.С., Хендрен Л., Кузинс С., Лотак О., де Мур О., Серени Д., Ситтампалам Г. и Тиббл Дж. 2005. Добавление сопоставления трассировки со свободными переменными в AspectJ. Архивировано 18 сентября 2009 г. на Wayback Machine . В материалах 20-й ежегодной конференции ACM SIGPLAN по объектно-ориентированному программированию, системам, языкам и приложениям (Сан-Диего, Калифорния, США, 16–20 октября 2005 г.). УПСЛА '05. ACM, Нью-Йорк, штат Нью-Йорк, 345–364.
- ^ Исторически показано в: Мейер, Арканзас; Стокмейер, Эл Джей (25 октября 1972 г.). «Проблема эквивалентности регулярных выражений с возведением в квадрат требует экспоненциального пространства». Труды 13-го ежегодного симпозиума по теории коммутации и автоматов (SWAT) . США: Компьютерное общество IEEE: 125–129. дои : 10.1109/SWAT.1972.29 . Современную презентацию см. в [1]
- ^ Альварес, Карме; Дженнер, Биргит (4 января 1993 г.). «Очень жесткий класс подсчета пространства журнала» . Теоретическая информатика . 107 (1): 3–30. дои : 10.1016/0304-3975(93)90252-О . ISSN 0304-3975 .
Ссылки
[ редактировать ]- М. О. Рабин и Д. Скотт, «Конечные автоматы и проблемы их принятия решений», IBM Journal of Research and Development , 3 :2 (1959), стр. 115–125.
- Майкл Сипсер, Введение в теорию вычислений . PWS, Бостон. 1997. ISBN 0-534-94728-X . (см. раздел 1.2: Недетерминизм, стр. 47–63.)
- Джон Э. Хопкрофт и Джеффри Д. Уллман, Введение в теорию автоматов, языки и вычисления , издательство Addison-Wesley Publishing, Ридинг, Массачусетс, 1979. ISBN 0-201-02988-X . (См. главу 2.)









































































































