Вращающиеся суппорты

В вычислительной геометрии метод вращающихся штангенциркулей — это метод разработки алгоритмов , который можно использовать для решения задач оптимизации, включая определение ширины или диаметра набора точек.

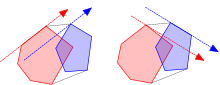
Метод назван так потому, что его идея аналогична вращению подпружиненного штангенциркуля вокруг внешней стороны выпуклого многоугольника . ^[1] Каждый раз, когда одно лезвие штангенциркуля прилегает плашмя к краю многоугольника, оно образует антиподальную пару , при этом острие или край касается противоположного лезвия. Полное «поворот» калипера вокруг многоугольника обнаруживает все противоположные пары; совокупность всех пар, рассматриваемая в виде графа, образует трекл . Метод вращающихся измерителей можно интерпретировать как проективный аналог алгоритма развертки линии , в котором развертка осуществляется по наклонам линий, а не по $координатам x$ или $y$ точек.

История [ править ]

Метод вращающихся штангенциркулей впервые был использован в диссертации Майкла Шамоса в 1978 году. ^[2] Шамос использовал этот метод для создания всех пар противоположных точек выпуклого многоугольника и для вычисления диаметра выпуклого многоугольника в $O(n)$ время. Годфрид Туссен придумал фразу «вращающиеся штангенциркули» и продемонстрировал, что этот метод применим для решения многих других задач вычислительной геометрии. ^[3]

Алгоритм Шамоса [ править ]

Шамос в своей диссертации (стр. 77–82) предложил следующий алгоритм метода вращающихся штангенциркулей, который генерировал все антиподальные пары вершин на выпуклом многоугольнике: ^[2]

/* p[] is in standard form, ie, counter clockwise order, 
     distinct vertices, no collinear vertices.
   ANGLE(m, n) is a procedure that returns the clockwise angle 
     swept out by a ray as it rotates from a position parallel 
     to the directed segment Pm,Pm+1 to a position parallel to Pn, Pn+1
   We assume all indices are reduced to mod N (so that N+1 = 1).
*/
GetAllAntiPodalPairs(p[1..n])
    // Find first anti-podal pair by locating vertex opposite P1
    i = 1
    j = 2
    while angle(i, j) < pi
        j++
    yield i, j

    /* Now proceed around the polygon taking account of
         possibly parallel edges. Line L passes through
         Pi, Pi+1 and M passes through Pj, Pj+1
    */

    // Loop on j until all of P has been scanned
    current = i    
    while j != n
        if angle(current, i + 1) <= angle(current, j + 1)
            j++
            current = j
        else
            i++
            current = i
        yield i, j

        // Now take care of parallel edges
        if angle(current, i + 1) = angle(current, j + 1)
            yield i + 1, j
            yield i, j + 1
            yield i + 1, j + 1
            if current = i
                j++
            else
                i++

Другая версия этого алгоритма появилась в тексте Препараты и Шамоса в 1985 году, в которой не вычислялись углы: ^[4]

GetAllAntiPodalPairs(p[1..n])
    i0 = n
    i = 1
    j = i + 1
    while (Area(i, i + 1, j + 1) > Area(i, i + 1, j))
        j = j + 1
        j0 = j
    while (i != j0)
        i = i + 1
        yield i, j
        while (Area(i, i + 1, j + 1) > Area(i, i + 1, j))
            j = j + 1
            if ((i, j) != (j0, i0))
                yield i, j
            else 
                return
        if (Area(j, i + 1, j + 1) = Area(i, i + 1, j))
            if ((i, j) != (j0, i0))
                yield i, j + 1
            else 
                yield i + 1, j

Приложения [ править ]

Пирзаде ^[5] описывает различные применения метода вращающихся штангенциркулей.

Расстояния [ править ]

Диаметр (максимальная ширина) выпуклого многоугольника ^[6]^[7]
Ширина ( минимальная ширина ) выпуклого многоугольника ^[8]
Максимальное расстояние между двумя выпуклыми многоугольниками ^[9]^[10]
Минимальное расстояние между двумя выпуклыми многоугольниками ^[11]^[12]
Самая широкая пустая (или разделяющая) полоса между двумя выпуклыми многоугольниками (упрощенный низкоразмерный вариант проблемы, возникающей при машинном обучении на основе опорных векторов )
Расстояние Гренандера между двумя выпуклыми многоугольниками ^[13]
Оптимальное разделение полос (используется в медицинской визуализации и твердотельном моделировании) ^[14]

Ограничительные рамки [ править ]

минимальную площадь Ограничительная рамка, ориентированная на
минимальному периметру Ограничительная рамка, ориентированная по

Триангуляции [ править ]

Луковые триангуляции
Спиральные триангуляции
Квадрангуляция
Хорошая триангуляция
Проблема с картинной галереей
Задача оптимизации размещения клина ^[15]

Многополигональные операции [ править ]

Объединение двух выпуклых многоугольников
Общие касательные к двум выпуклым многоугольникам
Пересечение двух выпуклых многоугольников ^[16]
Критические опорные линии двух выпуклых многоугольников
Векторные суммы (или сумма Минковского) двух выпуклых многоугольников ^[17]
Выпуклая оболочка двух выпуклых многоугольников

Обходы [ править ]

Кратчайшие трансверсали ^[18]^[19]
Трансверсали из тончайших полос ^[20]

Другие [ править ]

Непараметрические правила принятия решений для машинной классификации ^[21]
Оптимизация угла апертуры для решения проблем видимости в компьютерном зрении ^[22]
Найдены самые длинные клетки среди миллионов биологических клеток ^[23]
Сравнение точности двух человек на стрельбище
Классифицируйте участки мозга по сканированным изображениям

См. также [ править ]

Ссылки [ править ]

^ «Вращающиеся суппорты» на домашней странице Туссена.
↑ Перейти обратно: Перейти обратно: ^а ^б Шамос, Майкл (1978). «Вычислительная геометрия» (PDF) . Йельский университет. стр. 76–81.
^ Туссен, Годфрид Т. (1983). «Решение геометрических задач с вращающимися суппортами». В Протонотариосе, EN; Стассинопулос, Г.И.; Чиваллери, П.П. (ред.). Материалы MELECON '83, Средиземноморской электротехнической конференции, Афины, Греция, 24–26 мая 1983 г. IEEE. стр. A10.02/1–4. CiteSeerX 10.1.1.155.5671 .
^ Шамос, Франко П. Подготовьтесь, Майкл Ян (1985). Введение в вычислительную геометрию . Нью-Йорк, штат Нью-Йорк: Springer New York. ISBN 978-1-4612-7010-2 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Пирзаде, Хормоз (1999). Вычислительная геометрия с вращающимися штангенциркулями (Магистерская диссертация). Университет Макгилла.
^ Бинай К. Бхаттачарья и Годфрид Т. Туссен, «Быстрые алгоритмы вычисления диаметра конечного плоского множества», The Visual Computer , Vol. 3, № 6, май 1988 г., стр. 379–388.
^ Бинай К. Бхаттачарья и Годфрид Т. Туссен, «Противоположный пример алгоритму диаметра для выпуклых многоугольников», Транзакции IEEE по анализу шаблонов и машинному интеллекту , Vol. ПАМИ-4, № 3, май 1982 г., стр. 306–309.
^ Майкл Э. Хоул и Годфрид Т. Туссен, «Вычисление ширины набора», Транзакции IEEE по анализу шаблонов и машинному интеллекту , Том. 10, нет. 5 сентября 1988 г., стр. 761–765.
^ Годфрид Т. Туссен и Джим А. Макалир, «Простой алгоритм O ( n log n ) для поиска максимального расстояния между двумя конечными плоскими наборами», Pattern Recognition Letters , Vol. 1, 1982, стр. 21–24.
^ Бинай К. Бхаттачарья и Годфрид Т. Туссен, «Эффективные алгоритмы вычисления максимального расстояния между двумя конечными плоскими множествами», Journal of Algorithms , vol. 14, 1983, стр. 121–136.
^ Годфрид Т. Туссен и Бинай К. Бхаттачарья, «Оптимальные алгоритмы для вычисления минимального расстояния между двумя конечными плоскими множествами», Pattern Recognition Letters , vol. 2, декабрь 1983 г., стр. 79–82.
^ «Вращающиеся суппорты» . 30 марта 2015 г. Архивировано из оригинала 30 марта 2015 г. Проверено 22 марта 2017 г. {{cite web}}: CS1 maint: bot: исходный статус URL неизвестен ( ссылка )
^ МАРТИНЕС, УГО М. (1 января 1978 г.). «Обзор книги У. Гренандера «СИНТЕЗ ОБРАЗЦА», Springer-Verlag, Нью-Йорк, 1976. 509 стр.». Международный журнал общих систем . 4 (2): 126–127. дои : 10.1080/03081077808960672 . ISSN 0308-1079 .
^ Барекет и Вулферс (1998). «Оптимизация полосы, разделяющей два полигона» . Графические модели и обработка изображений . 60 (3): 214–221. дои : 10.1006/gmip.1998.0470 .
^ Тайхманн, Марек (1989). Проблемы оптимизации размещения клиньев (магистерская диссертация). Университет Макгилла.
^ Годфрид Т. Туссен, «Простой линейный алгоритм пересечения выпуклых многоугольников», The Visual Computer , Vol. 1, 1985, стр. 118–123.
^ Томас Лозано-Перес, «Пространственное планирование: подход к пространству конфигурации», Транзакции IEEE на компьютерах , Vol. 32, № 2, 1983, стр. 108–120.
^ Бинай К. Бхаттачарья и Годфрид Т. Туссен, «Вычисление кратчайших трансверсалей», Computing , vol. 46, 1991, стр. 93–119.
^ Бинай К. Бхаттачарья, Юрек Чизович, Питер Эдьед, Иван Стойменович, Годфрид Т. Туссен и Хорхе Уррутиа, «Вычисление кратчайших трансверсалей множеств», Международный журнал вычислительной геометрии и приложений , Vol. 2, № 4, декабрь 1992 г., стр. 417–436.
^ Жан-Марк Робер и Годфрид Т. Туссен, «Линейная аппроксимация простых объектов», Вычислительная геометрия: теория и приложения , Vol. 4, 1994, стр. 27–52.
^ Рассон и Гранвилл (1996). «Геометрические инструменты в классификации». Вычислительная статистика и анализ данных . 23 (1): 105–123. дои : 10.1016/S0167-9473(96)00024-2 .
^ Бозе, П.; Уртадо-Диас, Ф.; Омана-Пулидо, Э.; Снойинк, Дж.; Туссен, GT (1 августа 2002 г.). «Некоторые проблемы оптимизации угла апертуры». Алгоритмика . 33 (4): 411–435. CiteSeerX 10.1.1.16.7118 . дои : 10.1007/s00453-001-0112-9 . ISSN 0178-4617 . S2CID 27455160 .
^ «Алгоритмы неправильного определения диаметра выпуклых многоугольников» .

[1] «Вращающиеся суппорты» на домашней странице Туссена.

[shamos1978-2] Перейти обратно: Перейти обратно: ^а ^б Шамос, Майкл (1978). «Вычислительная геометрия» (PDF) . Йельский университет. стр. 76–81.

[tous83-3] Туссен, Годфрид Т. (1983). «Решение геометрических задач с вращающимися суппортами». В Протонотариосе, EN; Стассинопулос, Г.И.; Чиваллери, П.П. (ред.). Материалы MELECON '83, Средиземноморской электротехнической конференции, Афины, Греция, 24–26 мая 1983 г. IEEE. стр. A10.02/1–4. CiteSeerX 10.1.1.155.5671 .

[preparata1985-4] Шамос, Франко П. Подготовьтесь, Майкл Ян (1985). Введение в вычислительную геометрию . Нью-Йорк, штат Нью-Йорк: Springer New York. ISBN 978-1-4612-7010-2 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[pirzadeh1999-5] Пирзаде, Хормоз (1999). Вычислительная геометрия с вращающимися штангенциркулями (Магистерская диссертация). Университет Макгилла.

[6] Бинай К. Бхаттачарья и Годфрид Т. Туссен, «Быстрые алгоритмы вычисления диаметра конечного плоского множества», The Visual Computer , Vol. 3, № 6, май 1988 г., стр. 379–388.

[7] Бинай К. Бхаттачарья и Годфрид Т. Туссен, «Противоположный пример алгоритму диаметра для выпуклых многоугольников», Транзакции IEEE по анализу шаблонов и машинному интеллекту , Vol. ПАМИ-4, № 3, май 1982 г., стр. 306–309.

[8] Майкл Э. Хоул и Годфрид Т. Туссен, «Вычисление ширины набора», Транзакции IEEE по анализу шаблонов и машинному интеллекту , Том. 10, нет. 5 сентября 1988 г., стр. 761–765.

[9] Годфрид Т. Туссен и Джим А. Макалир, «Простой алгоритм O ( n log n ) для поиска максимального расстояния между двумя конечными плоскими наборами», Pattern Recognition Letters , Vol. 1, 1982, стр. 21–24.

[10] Бинай К. Бхаттачарья и Годфрид Т. Туссен, «Эффективные алгоритмы вычисления максимального расстояния между двумя конечными плоскими множествами», Journal of Algorithms , vol. 14, 1983, стр. 121–136.

[11] Годфрид Т. Туссен и Бинай К. Бхаттачарья, «Оптимальные алгоритмы для вычисления минимального расстояния между двумя конечными плоскими множествами», Pattern Recognition Letters , vol. 2, декабрь 1983 г., стр. 79–82.

[12] «Вращающиеся суппорты» . 30 марта 2015 г. Архивировано из оригинала 30 марта 2015 г. Проверено 22 марта 2017 г. {{cite web}}: CS1 maint: bot: исходный статус URL неизвестен ( ссылка )

[13] МАРТИНЕС, УГО М. (1 января 1978 г.). «Обзор книги У. Гренандера «СИНТЕЗ ОБРАЗЦА», Springer-Verlag, Нью-Йорк, 1976. 509 стр.». Международный журнал общих систем . 4 (2): 126–127. дои : 10.1080/03081077808960672 . ISSN 0308-1079 .

[14] Барекет и Вулферс (1998). «Оптимизация полосы, разделяющей два полигона» . Графические модели и обработка изображений . 60 (3): 214–221. дои : 10.1006/gmip.1998.0470 .

[15] Тайхманн, Марек (1989). Проблемы оптимизации размещения клиньев (магистерская диссертация). Университет Макгилла.

[16] Годфрид Т. Туссен, «Простой линейный алгоритм пересечения выпуклых многоугольников», The Visual Computer , Vol. 1, 1985, стр. 118–123.

[17] Томас Лозано-Перес, «Пространственное планирование: подход к пространству конфигурации», Транзакции IEEE на компьютерах , Vol. 32, № 2, 1983, стр. 108–120.

[18] Бинай К. Бхаттачарья и Годфрид Т. Туссен, «Вычисление кратчайших трансверсалей», Computing , vol. 46, 1991, стр. 93–119.

[19] Бинай К. Бхаттачарья, Юрек Чизович, Питер Эдьед, Иван Стойменович, Годфрид Т. Туссен и Хорхе Уррутиа, «Вычисление кратчайших трансверсалей множеств», Международный журнал вычислительной геометрии и приложений , Vol. 2, № 4, декабрь 1992 г., стр. 417–436.

[20] Жан-Марк Робер и Годфрид Т. Туссен, «Линейная аппроксимация простых объектов», Вычислительная геометрия: теория и приложения , Vol. 4, 1994, стр. 27–52.

[21] Рассон и Гранвилл (1996). «Геометрические инструменты в классификации». Вычислительная статистика и анализ данных . 23 (1): 105–123. дои : 10.1016/S0167-9473(96)00024-2 .

[22] Бозе, П.; Уртадо-Диас, Ф.; Омана-Пулидо, Э.; Снойинк, Дж.; Туссен, GT (1 августа 2002 г.). «Некоторые проблемы оптимизации угла апертуры». Алгоритмика . 33 (4): 411–435. CiteSeerX 10.1.1.16.7118 . дои : 10.1007/s00453-001-0112-9 . ISSN 0178-4617 . S2CID 27455160 .

[23] «Алгоритмы неправильного определения диаметра выпуклых многоугольников» .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]