Алгоритм, не обращающий внимания на кэш

В вычислениях алгоритм, не учитывающий кэш (или алгоритм, трансцендентный к кэшу), представляет собой алгоритм, процессора разработанный для использования преимуществ кэша без указания размера кэша (или длины строк кэша и т. д.) в качестве явного параметра. Оптимальный алгоритм без учета кэша — это алгоритм без учета кэша, который оптимально использует кэш (в асимптотическом смысле, игнорируя постоянные факторы). Таким образом, алгоритм без учета кэша предназначен для хорошей работы без изменений на нескольких машинах с разными размерами кэша или для иерархии памяти с разными уровнями кэша, имеющими разные размеры. Алгоритмы, не обращающие внимания на кэш, противопоставляются явному циклическому разбиению на блоки, которое явно разбивает задачу на блоки оптимального размера для данного кэша.

Оптимальные алгоритмы, не учитывающие кэш, известны для решения умножения матриц , транспонирования матриц , сортировки и ряда других задач. Некоторые более общие алгоритмы, такие как БПФ Кули-Тьюки , оптимально не обращают внимания на кэш при определенном выборе параметров. Поскольку эти алгоритмы оптимальны только в асимптотическом смысле (без учета постоянных факторов), дальнейшая настройка для получения почти оптимальной производительности в абсолютном смысле может потребоваться для конкретной машины. Цель алгоритмов, не учитывающих кэш, — уменьшить объем необходимой настройки.

Обычно алгоритм, не учитывающий кэш, работает по принципу рекурсивного алгоритма «разделяй и властвуй» , где проблема делится на все более мелкие подзадачи. В конце концов, достигается размер подзадачи, который помещается в кеш, независимо от размера кеша. Например, оптимальное умножение матриц без учета кэша достигается путем рекурсивного деления каждой матрицы на четыре подматрицы для умножения, умножая подматрицы в глубину . ^{[ нужна ссылка ]} При настройке для конкретной машины можно использовать гибридный алгоритм , который использует мозаику циклов, настроенную для конкретных размеров кэша на нижнем уровне, но в остальном использует алгоритм без учета кэша.

История

Идея (и название) алгоритмов, не обращающих внимания на кэш, была задумана Чарльзом Э. Лейзерсоном еще в 1996 году и впервые опубликована Харальдом Прокопом в его магистерской диссертации в Массачусетском технологическом институте в 1999 году. ^[1] Было много предшественников, обычно анализировавших конкретные проблемы; они подробно обсуждаются в Frigo et al. 1999. Среди первых цитируемых примеров - Синглтон 1969 года для рекурсивного быстрого преобразования Фурье, аналогичные идеи в Aggarwal et al. 1987 г., Фриго 1996 г. за умножение матриц и LU-разложение, а также Тодд Вельдхейзен 1996 г. за матричные алгоритмы в библиотеке Blitz++ .

Идеализированная модель кэша

В общем, программу можно сделать более ориентированной на кэш: ^[2]

Временная локальность , когда алгоритм извлекает одни и те же фрагменты памяти несколько раз;
Пространственная локальность , при которой последующие обращения к памяти происходят по соседним или близким адресам памяти .

Алгоритмы, не учитывающие кэш, обычно анализируются с использованием идеализированной модели кэша, иногда называемой моделью, не учитывающей кэш . Эту модель гораздо легче анализировать, чем характеристики реального кэша (которые имеют сложную ассоциативность, политику замены и т. д.), но во многих случаях доказуемо, что она находится в пределах постоянного коэффициента производительности более реалистичного кэша. Она отличается от модели внешней памяти , поскольку алгоритмы, не учитывающие кэш, не знают размера блока или размера кэша .

В частности, модель без учета кэша представляет собой абстрактную машину (т.е. теоретическую модель вычислений ). Это похоже на модель машины RAM , которая заменяет бесконечную ленту машины Тьюринга бесконечным массивом. К каждому местоположению в массиве можно получить доступ в $O(1)$ время, аналогичное оперативной памяти на реальном компьютере. В отличие от модели машины с ОЗУ, здесь также присутствует кеш: второй уровень хранения между ОЗУ и ЦП. Остальные различия между двумя моделями перечислены ниже. В модели без кэша:

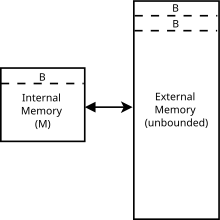
Память разбита на блоки $B$ объекты каждый.
Загрузка или сохранение между основной памятью и регистром ЦП теперь может обслуживаться из кэша.
Если загрузка или сохранение не могут быть обслужены из кэша, это называется промахом кэша .
Промах в кэше приводит к загрузке одного блока из основной памяти в кэш. А именно, если ЦП пытается получить доступ к слову $w$ и $x$ это строка, содержащая $w$ , затем $x$ загружается в кэш. Если кеш ранее был заполнен, строка также будет удалена (см. политику замены ниже).
Кэш вмещает $M$ объекты, где $M=\Omega (B^{2})$ . Это также известно как предположение о большом кэше .
Кэш полностью ассоциативен: каждая строка может быть загружена в любое место кэша. ^[3]
Политика замены оптимальна. Другими словами, предполагается, что в кэше задается вся последовательность обращений к памяти во время выполнения алгоритма. Если ему нужно выселить строку вовремя $t$ , он проверит последовательность будущих запросов и исключит строку, первый доступ к которой будет самым дальним в будущем. На практике это можно эмулировать с помощью политики «Наименее недавно использованное» , которая, как показано, находится в пределах небольшого постоянного коэффициента автономной стратегии оптимальной замены. ^[4]^[5]

Чтобы измерить сложность алгоритма, который выполняется в рамках модели без учета кэша, мы измеряем количество промахов в кэше , с которыми сталкивается алгоритм. Поскольку модель отражает тот факт, что доступ к элементам в кеше происходит намного быстрее, чем доступ к элементам в основной памяти , время работы алгоритма определяется только количеством передач памяти между кешем и основной памятью. Это похоже на модель внешней памяти , которая имеет все вышеперечисленные функции, но алгоритмы, не учитывающие кэш, не зависят от параметров кэша ( $B$ и $M$ ). ^[6] Преимущество такого алгоритма заключается в том, что то, что эффективно на машине, не обращающей внимания на кэш, вероятно, будет эффективно на многих реальных машинах без точной настройки конкретных параметров реальной машины. Для многих задач оптимальный алгоритм без учета кэша также будет оптимальным для машины с более чем двумя уровнями иерархии памяти . ^[4]

Примеры

Самый простой алгоритм без учета кэша, представленный Frigo et al. - это операция транспонирования неуместной матрицы ( для транспонирования также были разработаны алгоритмы на месте , но они намного сложнее для неквадратных матриц). Учитывая m × n массив A и n × m массив B , мы хотели бы сохранить транспонирование $A$ в $B.$ размером Наивное решение обходит один массив в порядке строк, а другой — в порядке столбцов. В результате, когда матрицы большие, мы получаем промах в кэше на каждом этапе обхода по столбцам. Общее количество промахов кэша равно $\Theta (mn)$ .

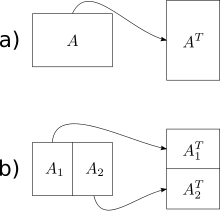
Алгоритм без учета кэша имеет оптимальную сложность работы. $O(mn)$ и оптимальная сложность кэша $O(1+mn/B)$ . Основная идея состоит в том, чтобы свести транспонирование двух больших матриц к транспонированию маленьких (суб)матриц. Мы делаем это, деля матрицы пополам по их большему размеру, пока нам не останется просто выполнить транспонирование матрицы, которая поместится в кеш. Поскольку размер кэша алгоритму неизвестен, матрицы будут продолжать рекурсивно делиться даже после этого момента, но эти дальнейшие подразделения будут находиться в кеше. Как только размеры $m$ и $n$ станут достаточно малы, входной массив размером $m\times n$ и выходной массив размером $n\times m$ вписывается в кеш, обход как по строкам, так и по столбцам приводит к $O(mn)$ работа и $O(mn/B)$ кэш промахивается. Используя этот подход «разделяй и властвуй», мы можем достичь того же уровня сложности для всей матрицы.

(В принципе, можно продолжать делить матрицы до тех пор, пока не будет достигнут базовый вариант размера 1×1, но на практике используется больший базовый случай (например, 16×16), чтобы амортизировать накладные расходы на рекурсивные вызовы подпрограмм.)

Большинство алгоритмов, не обращающих внимания на кеш, основаны на подходе «разделяй и властвуй». Они уменьшают проблему, так что в конечном итоге она помещается в кеш, независимо от того, насколько мал кеш, и заканчивают рекурсию с некоторым небольшим размером, определяемым накладными расходами на вызовы функций и аналогичными оптимизациями, не связанными с кешем, а затем используют некоторый доступ с эффективностью кеша. шаблон для объединения результатов этих небольших решенных задач.

Как и внешняя сортировка в модели внешней памяти , сортировка без учета кеша возможна в двух вариантах: сортировка воронкой , напоминающая сортировку слиянием ; и сортировка распределения без учета кеша , которая напоминает быструю сортировку . Как и их аналоги с внешней памятью, оба достигают работы времени $O\left({\tfrac {N}{B}}\log _{\tfrac {M}{B}}{\tfrac {N}{B}}\right)$ , что соответствует нижней границе и, таким образом, является асимптотически оптимальным . ^[6]

Практичность

Эмпирическое сравнение двух алгоритмов на основе ОЗУ, одного с поддержкой кэша и двух алгоритмов без учета кэша, реализующих очереди приоритетов, показало, что: ^[7]

Алгоритмы, не обращающие внимания на кэш, работали хуже, чем алгоритмы на основе ОЗУ и алгоритмы с поддержкой кэша, когда данные помещались в основную память.
Алгоритм с поддержкой кэша не казался значительно более сложным в реализации, чем алгоритмы без учета кэша, и предлагал лучшую производительность во всех случаях, протестированных в исследовании.
Алгоритмы, не обращающие внимания на кэш, превосходили алгоритмы на основе ОЗУ, когда размер данных превышал размер основной памяти.

В другом исследовании сравнивались хеш-таблицы (с поддержкой ОЗУ или без поддержки кэша), B-деревья (с поддержкой кэша) и структура данных, не учитывающая кэш, называемая «набором Бендера». Как по времени выполнения, так и по использованию памяти, хэш-таблица была лучшей, за ней следовало B-дерево, а Bender установил худшее во всех случаях. Использование памяти для всех тестов не превышало основной памяти. Хэш-таблицы были описаны как простые в реализации, в то время как набор Бендера «требовал больших усилий для правильной реализации». ^[8]

См. также

Ссылки

^ Харальд Прокоп. Алгоритмы, не обращающие внимания на кэш . Магистерская диссертация, Массачусетский технологический институт. 1999.
^ Аскитис, Николас; Зобель, Джастин (2005). «Разрешение конфликтов с учетом кэша в строковых хэш-таблицах» . Международный симпозиум по обработке строк и поиску информации . Спрингер : 93. doi : 10.1007/11575832_1 . ISBN 978-3-540-29740-6 .
^ Кумар, Пиюш. «Алгоритмы, не обращающие внимания на кэш». Алгоритмы для иерархий памяти . LNCS 2625. Springer Verlag: 193–212. CiteSeerX 10.1.1.150.5426 .
^ Перейти обратно: ^а ^б Фриго, М.; Лейзерсон, CE ; Прокоп, Х. ; Рамачандран, С. (1999). Алгоритмы, не обращающие внимания на кэш (PDF) . Учеб. IEEE симп. по основам информатики (FOCS). стр. 285–297.
^ Дэниел Слитор, Роберт Тарджан. Амортизированная эффективность обновлений списков и правил разбиения на страницы . В «Сообщениях ACM» , том 28, номер 2, стр. 202–208. Февраль 1985 года.
^ Перейти обратно: ^а ^б Эрик Демейн . Алгоритмы и структуры данных, не обращающие внимания на кэш , в конспектах лекций Летней школы EEF по массивным наборам данных, БРИКС, Орхусский университет, Дания, 27 июня – 1 июля 2002 г.
^ Олсен, Джеспер Холм; Сков, Сорен Кристиан (2 декабря 2002 г.). Алгоритмы, не обращающие внимания на кэш, на практике (PDF) (магистр). Копенгагенский университет . Проверено 3 января 2022 г.
^ Вервер, Макс (23 июня 2008 г.). «Оценка структуры данных, не учитывающей кэш» (PDF) . Проверено 3 января 2022 г.

[Prokop-1] Харальд Прокоп. Алгоритмы, не обращающие внимания на кэш . Магистерская диссертация, Массачусетский технологический институт. 1999.

[nick05-2] Аскитис, Николас; Зобель, Джастин (2005). «Разрешение конфликтов с учетом кэша в строковых хэш-таблицах» . Международный симпозиум по обработке строк и поиску информации . Спрингер : 93. doi : 10.1007/11575832_1 . ISBN 978-3-540-29740-6 .

[Kumar-3] Кумар, Пиюш. «Алгоритмы, не обращающие внимания на кэш». Алгоритмы для иерархий памяти . LNCS 2625. Springer Verlag: 193–212. CiteSeerX 10.1.1.150.5426 .

[Frigo99-4] Перейти обратно: ^а ^б Фриго, М.; Лейзерсон, CE ; Прокоп, Х. ; Рамачандран, С. (1999). Алгоритмы, не обращающие внимания на кэш (PDF) . Учеб. IEEE симп. по основам информатики (FOCS). стр. 285–297.

[Sleator-5] Дэниел Слитор, Роберт Тарджан. Амортизированная эффективность обновлений списков и правил разбиения на страницы . В «Сообщениях ACM» , том 28, номер 2, стр. 202–208. Февраль 1985 года.

[Demaine02-6] Перейти обратно: ^а ^б Эрик Демейн . Алгоритмы и структуры данных, не обращающие внимания на кэш , в конспектах лекций Летней школы EEF по массивным наборам данных, БРИКС, Орхусский университет, Дания, 27 июня – 1 июля 2002 г.

[7] Олсен, Джеспер Холм; Сков, Сорен Кристиан (2 декабря 2002 г.). Алгоритмы, не обращающие внимания на кэш, на практике (PDF) (магистр). Копенгагенский университет . Проверено 3 января 2022 г.

[8] Вервер, Макс (23 июня 2008 г.). «Оценка структуры данных, не учитывающей кэш» (PDF) . Проверено 3 января 2022 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]