График сложенного куба

График сложенного куба
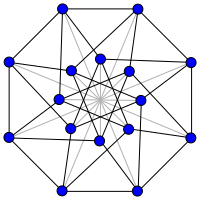Граф свернутого куба размерности 5 (т. е. граф Клебша ).
Вершины	$2^{n-1}$
Края	$2^{n-2}n$
Диаметр	$\left\lfloor {\frac {n}{2}}\right\rfloor$
Хроматическое число	${\begin{cases}2&{\text{even }}n\\4&{\text{odd }}n\end{cases}}$
Характеристики	Обычный гамильтониан Дистанционно-транзитивный .
Таблица графиков и параметров

В теории графов граф свернутого куба — это неориентированный граф, образованный из графа гиперкуба путем добавления к нему идеального паросочетания , соединяющего противоположные пары вершин гиперкуба.

Строительство

Граф свернутого куба размерности k (содержащий 2 ^{к - 1} вершины) могут быть образованы добавлением ребер между противоположными парами вершин в графе гиперкуба размерности k - 1. (В гиперкубе с 2 вершинами ^н вершин, пара вершин является противоположной, если кратчайший путь между ними имеет длину n .) Его можно, эквивалентно, сформировать из графа гиперкуба (также) размерности k , который имеет вдвое больше вершин, путем отождествления вместе (или стягивания ) каждая противоположная пара вершин.

Характеристики

Граф свернутого куба размерности k является k - регулярным с 2 ^{к - 1} вершины и 2 ^{к - 2} k ребер.

Хроматическое число графа свернутого куба размерности k равно двум, когда k четное (то есть в данном случае граф двудольный ), и четырем, когда k нечетное. Нечетный обхват сложенного куба нечетной размерности равен k , поэтому для нечетных k больше трех графы сложенных кубов представляют собой класс графов без треугольников с хроматическим номером четыре и сколь угодно большим нечетным обхватом. Как дистанционно-регулярный граф с нечетным обхватом k и диаметром ( k - 1)/2, сложенные кубы нечетной размерности являются примерами обобщенных нечетных графов .

Когда k нечетно, двудольное двойное покрытие сложенного куба размерности k представляет собой куб измерения k , из которого он был сформирован. Однако когда k четно, куб размерности k является двойным покрытием , а не двудольным двойным покрытием. В этом случае сложенный куб сам уже двудольный . Графы свернутых кубов наследуют от своих подграфов гиперкубов свойство иметь гамильтонов цикл , а от гиперкубов, которые дважды покрывают их, — свойство быть дистанционно-транзитивным графом .

Когда k нечетно, сложенный куб размерности k содержит в качестве подграфа полное двоичное дерево с 2 ^к − 1 узел. Однако, когда k четно, это невозможно, потому что в этом случае свернутый куб представляет собой двудольный граф с равным количеством вершин на каждой стороне двудольного деления, что сильно отличается от соотношения почти два к одному для двудольного графа. полное двоичное дерево.

Примеры

• Граф свернутого куба размерности три является полным графом K ₄ .
• Граф свернутого куба размерности четыре представляет собой полный двудольный граф K _4,4 .
• Граф свернутого куба размерности пять — это граф Клебша .
• Граф свернутого куба размерности шесть — это граф Куммера , то есть граф Леви конфигурации точки-плоскости Куммера .

Приложения

В параллельных вычислениях графы свернутых кубов изучались как потенциальная топология сети , как альтернатива гиперкубу. По сравнению с гиперкубом с сложенный куб тем же количеством узлов имеет почти ту же степень вершины, но только половину диаметра . эффективные распределенные алгоритмы (относительно гиперкуба ) для трансляции информации в свернутом кубе. Известны

См. также

• Граф половинного куба

Ссылки

• Ван Бон, Джон (2007), «Конечные примитивные дистанционно-транзитивные графы», European Journal of Combinatorics , 28 (2): 517–532, doi : 10.1016/j.ejc.2005.04.014 .
• Чудам, ЮАР; Нандини, Р. Уша (2004), «Полные двоичные деревья в сложенных и расширенных кубах», Networks , 43 (4): 266–272, doi : 10.1002/net.20002 , S2CID   6448906 .
• Ван Дам, Эдвин; Хемерс, Виллем Х. (2010), Нечетная характеристика обобщенных нечетных графов , Серия дискуссионных документов CentER № 2010-47, том. 2010–47, doi : 10.2139/ssrn.1596575 , SSRN   1596575 .
• Эль-Амави, А.; Латифи, С. (1991), «Свойства и характеристики свернутых гиперкубов», IEEE Trans. Параллельное распределение. Сист. , 2 (1): 31–42, дои : 10.1109/71.80187 .
• Годсил, Крис (2004), Интересные графики и их раскраски , CiteSeerX   10.1.1.91.6390 .
• Варваригос, Э. (1995), "Эффективные алгоритмы маршрутизации для сетей свернутого куба", Proc. 14-й Международный. Конференция Феникса. по компьютерам и коммуникациям , IEEE, стр. 143–151, doi : 10.1109/PCCC.1995.472498 , ISBN.  0-7803-2492-7 , S2CID   62407778 .

Внешние ссылки

• Вайсштейн, Эрик В. , «Граф сложенного куба» , MathWorld