Узловая матрица допуска

В энергетике узловая матрица адмиттансов (или просто матрица адмиттансов ) представляет собой размера N x N, матрицу описывающую линейную энергетическую систему с N шинами . Он представляет собой узловой доступ шин в энергосистему. В реальных системах, содержащих тысячи шин, матрица допуска довольно разрежена. Каждая шина в реальной энергосистеме обычно соединена только с несколькими другими шинами через линии электропередачи . ^[1] Узловая матрица адмиттансов используется при формулировке задачи о потоке мощности .

Построение из однолинейной схемы

Узловая матрица проводимостей энергосистемы представляет собой форму матрицы Лапласа узловой диаграммы проводимости энергосистемы, которая получается путем применения законов Кирхгофа к диаграмме проводимости энергосистемы. Исходя из однолинейной схемы энергосистемы, узловая диаграмма проводимости получается по формуле:

заменяя каждую линию на диаграмме ее эквивалентной проводимостью, и
преобразование всех источников напряжения в эквивалентный источник тока.

Рассмотрим граф адмиттанса с $N$ автобусы. Вектор напряжений шины , $V$ , является $N\times 1$ вектор где $V_{k}$ напряжение шины $k$ , и вектор подачи тока в шину , $I$ , является $N\times 1$ вектор где $I_{k}$ совокупный ток, подаваемый на шину $k$ всеми нагрузками и источниками, подключенными к шине. Пропуск между автобусами $k$ и $i$ это комплексное число $y_{ki}$ , и представляет собой сумму пропусков всех линий, соединяющих автобусы. $k$ и $i$ . Пропуск между автобусами $i$ и земля $y_{k}$ , и представляет собой сумму допусков всех нагрузок, подключенных к шине $k$ .

Рассмотрим текущий впрыск , $I_{k}$ , в автобус $k$ . Применение действующего закона Кирхгофа

I_{k}=\sum _{i=1,2,\ldots ,N}I_{ki}

где $I_{ki}$ ток от шины $k$ на автобус $i$ для $k\neq i$ и $I_{kk}$ ток от шины $k$ на землю через нагрузку шины. Применяя закон Ома к диаграмме проводимости, напряжения шины , а также линейные токи и токи нагрузки связаны соотношением

I_{ki}={\begin{cases}V_{k}{y_{k}},&{\mbox{if}}\quad i=k\\(V_{k}-V_{i})y_{ki},&{\mbox{if}}\quad i\neq k.\end{cases}}

Поэтому,

I_{k}=\sum _{i=1,2,\ldots ,N \atop i\neq k}{(V_{k}-V_{i})y_{ki}}+V_{k}y_{k}=V_{k}\left(y_{k}+\sum _{i=1,2,\ldots ,N \atop i\neq k}y_{ki}\right)-\sum _{i=1,2,\ldots ,N \atop i\neq k}V_{i}y_{ki}

Это соотношение можно кратко записать в матричной форме с использованием матрицы адмиттанса. Узловая матрица допуска $Y$ это $N\times N$ матрица такая, что напряжение на шине и подача тока удовлетворяют закону Ома

YV=I

в векторном формате. Записи $Y$ затем определяются уравнениями для токов, вводимых в шины, в результате чего

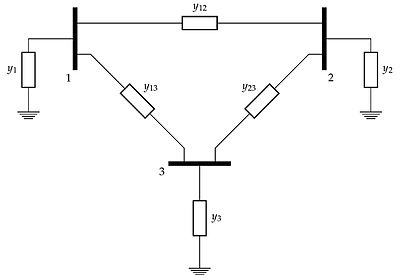
Y_{kj}={\begin{cases}y_{k}+\sum _{i=1,2,\ldots ,N \atop i\neq k}{y_{ki}},&{\mbox{if}}\quad k=j\\-y_{kj},&{\mbox{if}}\quad k\neq j.\end{cases}}

В качестве примера рассмотрим диаграмму допусков полностью подключенной сети с тремя шинами, показанной на рисунке 1. Матрица допусков, полученная из сети с тремя шинами на рисунке, равна:

Y={\begin{pmatrix}y_{1}+y_{12}+y_{13}&-y_{12}&-y_{13}\\-y_{12}&y_{2}+y_{12}+y_{23}&-y_{23}\\-y_{13}&-y_{23}&y_{3}+y_{13}+y_{23}\\\end{pmatrix}}

Диагональные записи $Y_{11},Y_{22},...,Y_{nn}$ называются самопропусками узлов сети. Недиагональные записи представляют собой взаимные пропускания узлов, соответствующих индексам записи. Матрица допуска $Y$ обычно представляет собой симметричную матрицу, поскольку $Y_{ki}=Y_{ik}$ . Однако расширение линейной модели может сделать $Y$ асимметричный. Например, моделирование фазосдвигающих трансформаторов приводит к получению эрмитовой матрицы проводимости. ^[2]

Приложения

Матрица адмиттансов чаще всего используется при формулировке задачи потока мощности . ^[3]^[4]

См. также

Ссылки

^ Грейнджер, Джон (1994). Анализ энергосистемы . МакГроу-Хилл Наука/инженерия/математика. ISBN 978-0070612938 .
^ Саадат, Хади (1999). «6.7 Переключающие трансформаторы». Анализ энергосистемы . Соединенное Королевство: WCB/McGraw-Hill. ISBN 978-0075616344 .
^ Маккалли, Джеймс. «Уравнения потока мощности» (PDF) . Инженерное дело штата Айова .
^ Саадат, Хади (1999). Анализ энергосистемы . Соединенное Королевство: WCB/McGraw-Hill. ISBN 978-0075616344 .

Внешние ссылки

Программа AC/C++ и исходный код для вычисления матриц Ybus и Zbus

[1] Грейнджер, Джон (1994). Анализ энергосистемы . МакГроу-Хилл Наука/инженерия/математика. ISBN 978-0070612938 .

[2] Саадат, Хади (1999). «6.7 Переключающие трансформаторы». Анализ энергосистемы . Соединенное Королевство: WCB/McGraw-Hill. ISBN 978-0075616344 .

[3] Маккалли, Джеймс. «Уравнения потока мощности» (PDF) . Инженерное дело штата Айова .

[4] Саадат, Хади (1999). Анализ энергосистемы . Соединенное Королевство: WCB/McGraw-Hill. ISBN 978-0075616344 .

[1]

[2]

[3]

[4]