Теорема ван Циттерта – Цернике

Пространственно некогерентный источник кажется (пространственно) когерентным, если смотреть издалека. На визуализации три источника (черные точки) некогерентны друг с другом, серые линии — это нули поля от каждого источника (в фиксированное время), а черная линия — ноль общего поля.

Теорема Ван Циттерта-Цернике , названная в честь физиков Питера Хендрика ван Циттерта и Фрица Цернике , ^[1] — это формула теории когерентности , которая утверждает, что при определенных условиях преобразование Фурье функции распределения интенсивности удаленного некогерентного источника равно его комплексной видимости . ^[2]^[3] Это означает, что волновой фронт от некогерентного источника будет казаться в основном когерентным на больших расстояниях. Интуитивно это можно понять, рассмотрев волновые фронты, создаваемые двумя некогерентными источниками. Если мы измеряем волновой фронт непосредственно перед одним из источников, в наших измерениях будет доминировать ближайший источник. Если мы проведем то же измерение вдали от источников, в наших измерениях больше не будет доминировать один источник; оба источника будут почти одинаково вносить вклад в волновой фронт на больших расстояниях.

Это рассуждение можно легко визуализировать, бросив два камня в центр спокойного пруда. Вблизи центра пруда возмущение, создаваемое двумя камнями, будет очень сложным. Однако по мере распространения возмущения к краю пруда волны сглаживаются и кажутся почти круглыми.

Теорема Ван Циттерта-Цернике имеет важные последствия для радиоастрономии . За исключением пульсаров и мазеров , все астрономические источники пространственно некогерентны. Тем не менее, поскольку они наблюдаются на расстояниях, достаточно больших, чтобы удовлетворять теореме Ван Циттерта – Цернике, эти объекты демонстрируют ненулевую степень когерентности в разных точках плоскости изображения. Измеряя степень когерентности в различных точках плоскости изображения (так называемая « функция видимости ») астрономического объекта, радиоастроном может тем самым восстановить распределение яркости источника и составить двумерную карту внешнего вида источника.

Формулировка теоремы

Рассмотрим две очень далекие параллельные плоскости, обе перпендикулярные лучу зрения, и назовем их исходной плоскостью и плоскостью наблюдения ; Если $\Gamma _{12}(u,v,0)$ — функция взаимной когерентности между двумя точками плоскости наблюдения, тогда

\Gamma _{12}(u,v,0)=\iint I(l,m)e^{-2\pi i(ul+vm)}\,dl\,dm

где $l$ и $m$ – направляющие косинусы точки удаленного источника в плоскости источника, $u$ и $v$ - соответственно расстояние x и расстояние y между двумя точками наблюдения на плоскости наблюдения в единицах длины волны и $I$ — интенсивность источника. ^[4] Эта теорема была впервые выведена Питером Хендриком ван Циттертом. ^[5] в 1934 году с более простым доказательством, предоставленным Фрицем Цернике в 1938 году. ^[6]

Эта теорема будет по-прежнему сбивать с толку некоторых инженеров и ученых из-за ее статистической природы и отличия от простых корреляционных или даже ковариационных методов обработки. Хорошим справочником (который, возможно, не прояснит проблему для некоторых пользователей, но содержит отличный набросок, поясняющий метод) — Goodman, начиная со страницы 207. ^[7]

Функция взаимной когерентности

Функция взаимной когерентности для некоторого электрического поля $E(t)$ измеренный в двух точках плоскости наблюдения (назовем их 1 и 2), определяется как

\Gamma _{12}(\tau )=\lim _{T\to \infty }{\frac {1}{2T}}\int _{-T}^{T}E_{1}(t)E_{2}^{*}(t-\tau )dt

где $\tau$ это временной сдвиг между измерениями $E(t)$ в точках наблюдения 1 и 2. Взаимную когерентность поля в двух точках можно рассматривать как усредненную по времени взаимную корреляцию между электрическими полями в двух точках, разделенных во времени на $\tau$ . Таким образом, если мы наблюдаем два полностью некогерентных источника, мы должны ожидать, что функция взаимной когерентности будет относительно небольшой между двумя случайными точками в плоскости наблюдения, поскольку источники будут интерферировать как деструктивно, так и конструктивно. Однако вдали от источников следует ожидать, что функция взаимной когерентности будет относительно большой, поскольку сумма наблюдаемых полей будет почти одинаковой в любых двух точках.

Нормализация функции взаимной когерентности на произведение квадратных корней из напряженностей двух электрических полей дает комплексную степень когерентности (второго порядка) (функцию коэффициента корреляции):

\gamma _{12}(\tau )={\frac {\Gamma _{12}(\tau )}{{\sqrt {I_{1}}}{\sqrt {I_{2}}}}}

Доказательство теоремы

Позволять $XY$ и $xy$ быть соответственно декартовыми координатами плоскости источника и плоскости наблюдения. Предположим, что электрическое поле, создаваемое некоторой точкой источника в плоскости источника, измеряется в двух точках: $P_{1}$ и $P_{2}$ , в плоскости наблюдения. Положение точки в источнике можно обозначить ее направляющими косинусами. $(l,m)$ . (Поскольку источник находится далеко, его направление должно быть одинаковым при $P_{1}$ как в $P_{2}$ .) Электрическое поле, измеренное при $P_{1}$ затем можно записать с помощью векторов :

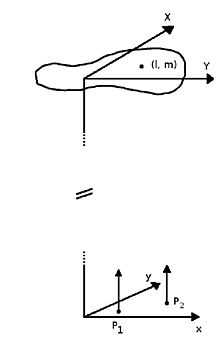
E_{1}(l,m,t)=A\left(l,m,t-{\frac {R_{1}}{c}}\right){\frac {e^{-i\omega \left(t-{\frac {R_{1}}{c}}\right)}}{R_{1}}}

где $R_{1}$ расстояние от источника до $P_{1}$ , $\omega$ - угловая частота света , а $A$ – комплексная амплитуда электрического поля. Аналогично, электрическое поле, измеренное при $P_{2}$ можно записать как

E_{2}(l,m,t)=A\left(l,m,t-{\frac {R_{2}}{c}}\right){\frac {e^{-i\omega \left(t-{\frac {R_{2}}{c}}\right)}}{R_{2}}}

Вычислим теперь усредненную по времени взаимную корреляцию между электрическим полем при $P_{1}$ и $P_{2}$ :

{\big \langle }E_{1}(l,m,t)E_{2}^{*}(l,m,t){\big \rangle }={\Bigg \langle }A\left(l,m,t-{\frac {R_{1}}{c}}\right)A^{*}\left(l,m,t-{\frac {R_{2}}{c}}\right){\Bigg \rangle }\times {\frac {e^{i\omega {\frac {R_{1}}{c}}}}{R_{1}}}\times {\frac {e^{-i\omega {\frac {R_{2}}{c}}}}{R_{2}}}

Поскольку величина в угловых скобках усреднена по времени, к временному члену амплитуд может быть добавлено произвольное смещение, при условии, что к обоим добавляется одно и то же смещение. Давайте теперь добавим ${\frac {R_{1}}{c}}$ к временному члену обеих амплитуд. Таким образом, усредненная по времени взаимная корреляция электрического поля в двух точках упрощается до

{\big \langle }E_{1}(l,m,t)E_{2}^{*}(l,m,t){\big \rangle }={\Bigg \langle }A(l,m,t)A^{*}\left(l,m,t-{\frac {R_{2}-R_{1}}{c}}\right){\Bigg \rangle }\times {\frac {e^{i\omega \left({\frac {R_{1}-R_{2}}{c}}\right)}}{R_{1}R_{2}}}

Но если источник находится в дальней зоне , то разница между $R_{1}$ и $R_{2}$ будет мал по сравнению с расстоянием, которое свет проходит во времени. $t$ . ( $t$ имеет тот же порядок, что и обратная полоса пропускания .) Поэтому этой небольшой поправкой можно пренебречь, что еще больше упростит наше выражение для взаимной корреляции электрического поля при $P_{1}$ и $P_{2}$ к

\langle E_{1}(l,m,t)E_{2}^{*}(l,m,t)\rangle =\langle A(l,m,t)A^{*}(l,m,t)\rangle \times {\frac {e^{i\omega \left({\frac {R_{1}-R_{2}}{c}}\right)}}{R_{1}R_{2}}}

Сейчас, $\langle A(l,m,t)A^{*}(l,m,t)\rangle$ это просто интенсивность источника в определенной точке, $I(l,m)$ . Таким образом, наше выражение для взаимной корреляции еще больше упрощается до

\langle E_{1}(l,m,t)E_{2}^{*}(l,m,t)\rangle =I(l,m){\frac {e^{i\omega \left({\frac {R_{1}-R_{2}}{c}}\right)}}{R_{1}R_{2}}}

Чтобы вычислить функцию взаимной когерентности из этого выражения, просто проинтегрируйте по всему источнику.

\Gamma _{12}(u,v,0)=\iint _{\textrm {source}}I(l,m){\frac {e^{i\omega \left({\frac {R_{1}-R_{2}}{c}}\right)}}{R_{1}R_{2}}}\,dS

Обратите внимание, что перекрестные члены формы $\langle A_{1}(l,m,t)A_{2}^{*}(l,m,t)\rangle$ не включены из-за предположения, что источник некогерентен. Таким образом, усредненная по времени корреляция между двумя разными точками источника будет равна нулю.

Далее перепишите $R_{2}-R_{1}$ термин с использованием $u,v,l$ и $m$ . Для этого позвольте $P_{1}=(x_{1},y_{1})$ и $P_{2}=(x_{2},y_{2})$ . Это дает

R_{1}={\sqrt {R^{2}+x_{1}^{2}+y_{1}^{2}}}\,

R_{2}={\sqrt {R^{2}+x_{2}^{2}+y_{2}^{2}}}\,

где $R$ – расстояние между центром плоскости наблюдения и центром источника. Разница между $R_{1}$ и $R_{2}$ таким образом становится

R_{2}-R_{1}=R{\sqrt {1+{\frac {x_{2}^{2}}{R^{2}}}+{\frac {y_{2}^{2}}{R^{2}}}}}-R{\sqrt {1+{\frac {x_{1}^{2}}{R^{2}}}+{\frac {y_{1}^{2}}{R^{2}}}}}

Но потому что $x_{1},x_{2},y_{1}$ и $y_{2}$ все гораздо меньше, чем $R$ , квадратные корни можно разложить по Тейлору , что приведет к первому порядку

R_{2}-R_{1}=R\left(1+{\frac {1}{2}}\left({\frac {x_{2}^{2}+y_{2}^{2}}{R^{2}}}\right)\right)-R\left(1+{\frac {1}{2}}\left({\frac {x_{1}^{2}+y_{1}^{2}}{R^{2}}}\right)\right)

что после некоторых алгебраических манипуляций упрощается до

R_{2}-R_{1}={\frac {1}{2R}}\left((x_{2}-x_{1})(x_{2}+x_{1})+(y_{2}-y_{1})(y_{2}+y_{1})\right)

Сейчас, ${\frac {1}{2}}(x_{2}+x_{1})$ это середина вдоль $x$ -ось между $P_{1}$ и $P_{2}$ , так ${\frac {1}{2R}}(x_{2}+x_{1})$ дает нам $l$ , один из направляющих косинусов к источникам. Сходным образом, $m={\frac {1}{2R}}(y_{2}+y_{1})$ . Более того, напомним, что $u$ определялось как количество длин волн вдоль $x$ -ось между $P_{1}$ и $P_{2}$ . Так

u={\frac {\omega }{2\pi c}}(x_{1}-x_{2})

Сходным образом, $v$ количество длин волн между $P_{1}$ и $P_{2}$ вдоль $y$ -ось, поэтому

v={\frac {\omega }{2\pi c}}(y_{1}-y_{2})

Следовательно

R_{2}-R_{1}={\frac {2\pi c}{\omega }}(ul+vm)

Потому что $x_{1},x_{2},y_{1},$ и $y_{2}$ все гораздо меньше, чем $R$ , $R_{1}\simeq R_{2}\simeq R$ . Дифференциальный элемент площади, $dS$ , тогда можно записать как дифференциальный элемент угла телесного $R^{2}\,dl\,dm$ . Наше выражение для функции взаимной когерентности принимает вид

\Gamma _{12}(u,v,0)=\iint _{\textrm {source}}I(l,m)e^{-{\frac {i\omega }{c}}{\frac {2\pi c}{\omega }}(ul+vm)}\,dl\,dm

Что сводится к

\Gamma _{12}(u,v,0)=\iint _{\textrm {source}}I(l,m)e^{-2\pi i(ul+vm)}\,dl\,dm

Но пределы этих двух интегралов могут быть расширены, чтобы охватить всю плоскость источника, если функция интенсивности источника установлена равной нулю в этих областях. Следовательно,

\Gamma _{12}(u,v,0)=\iint I(l,m)e^{-2\pi i(ul+vm)}\,dl\,dm

что представляет собой двумерное преобразование Фурье функции интенсивности. Это завершает доказательство.

Предположения теоремы

Теорема ван Циттерта-Цернике основана на ряде предположений, каждое из которых приблизительно верно почти для всех астрономических источников. Здесь обсуждаются наиболее важные предположения теоремы и их отношение к астрономическим источникам.

Некогерентность источника

Пространственно когерентный источник не подчиняется теореме Ван Циттерта – Цернике. Чтобы понять, почему это так, предположим, что мы наблюдаем источник, состоящий из двух точек: $a$ и $b$ . Вычислим функцию взаимной когерентности между $P_{1}$ и $P_{2}$ в плоскости наблюдения. По принципу суперпозиции электрическое поле при $P_{1}$ является

E_{1}=E_{a1}+E_{b1}

и в $P_{2}$ является

E_{2}=E_{a2}+E_{b2}

поэтому функция взаимной когерентности равна

\langle E_{1}(t)E_{2}^{*}(t-\tau )\rangle =\langle (E_{a1}(t)+E_{b1}(t))(E_{a2}^{*}(t-\tau )+E_{b2}^{*}(t-\tau ))\rangle

Что становится

\langle E_{1}(t)E_{2}^{*}(t-\tau )\rangle =\langle E_{a1}(t)E_{a2}^{*}(t-\tau )\rangle +\langle E_{a1}(t)E_{b2}^{*}(t-\tau )\rangle +\langle E_{b1}(t)E_{a2}^{*}(t-\tau )\rangle +\langle E_{b1}(t)E_{b2}^{*}(t-\tau )\rangle

Если точки $a$ и $b$ когерентны, то перекрестные члены в приведенном выше уравнении не обращаются в нуль. В этом случае, когда мы вычисляем функцию взаимной когерентности для расширенного когерентного источника, мы не сможем просто интегрировать функцию интенсивности источника; наличие ненулевых перекрестных членов придало бы функции взаимной когерентности непростую форму.

Это предположение справедливо для большинства астрономических источников. Пульсары и мазеры — единственные астрономические источники, демонстрирующие когерентность.

Расстояние до источника

При доказательстве теоремы мы предполагаем, что $R\gg x_{1}-x_{2}$ и $R\gg y_{1}-y_{2}$ . То есть мы предполагаем, что расстояние до источника намного больше размера области наблюдения. Точнее, теорема Ван Циттерта–Цернике требует, чтобы мы наблюдали источник в так называемом дальнем поле. Следовательно, если $D$ — характерный размер области наблюдения (например, в случае двухзеркального радиотелескопа — длина базовой линии между двумя телескопами), тогда

R\gg {\frac {D^{2}}{\lambda }}

Используя разумную базовую линию в 20 км для Очень Большой Решётки на длине волны 1 см, расстояние в дальней зоне будет порядка $4\times 10^{10}$ м. Следовательно, любой астрономический объект, находящийся дальше парсека, находится в дальнем поле. Однако объекты Солнечной системы не обязательно находятся в дальней зоне, и поэтому теорема Ван Циттерта – Цернике к ним не применима.

Угловой размер источника

При выводе теоремы Ван Циттерта–Цернике запишем направляющие косинусы $l$ и $m$ как ${\frac {1}{2}}(x_{1}+x_{2})/R$ и ${\frac {1}{2}}(y_{1}+y_{2})/R$ . Однако существует третий направляющий косинус, которым пренебрегают, поскольку $R\gg {\frac {1}{2}}(x_{1}+x_{2})$ и $R\gg {\frac {1}{2}}(y_{1}+y_{2})$ ; в этих предположениях оно очень близко к единице. Но если источник имеет большую угловую протяженность, мы не можем пренебрегать этим косинусом третьего направления, и теорема Ван Циттерта – Цернике больше не выполняется.

Поскольку большинство астрономических источников образуют на небе очень малые углы (обычно намного меньше градуса), это предположение теоремы легко выполняется в области радиоастрономии.

Квазимонохроматические волны

Теорема Ван Циттерта – Цернике предполагает, что источник квазимонохроматичен. То есть, если источник излучает свет в диапазоне частот, $\Delta \nu$ , со средней частотой $\nu$ , то оно должно удовлетворять

{\frac {\Delta \nu }{\nu }}\lesssim 1

Более того, полоса пропускания должна быть достаточно узкой, чтобы

{\frac {\Delta \nu }{\nu }}\ll {\frac {1}{lu}}

где $l$ это снова направляющий косинус, указывающий размер источника и $u$ - это количество длин волн между одним концом апертуры и другим. Без этого предположения мы не можем пренебречь $(R_{2}-R_{1})/c$ по сравнению с $t$

Это требование подразумевает, что радиоастроном должен ограничивать сигналы посредством полосового фильтра . Поскольку радиотелескопы почти всегда пропускают сигнал через относительно узкий полосовой фильтр, на практике это предположение обычно выполняется.

Двумерный источник

Мы предполагаем, что наш источник лежит в двумерной плоскости. На самом деле астрономические источники трехмерны. Однако, поскольку они находятся в дальней зоне, их угловое распределение не меняется с расстоянием. Поэтому, когда мы измеряем астрономический источник, его трехмерная структура проецируется на двухмерную плоскость. Это означает, что теорема Ван Циттерта – Цернике может быть применена к измерениям астрономических источников, но мы не можем определить структуру на луче зрения с помощью таких измерений.

Однородность среды

Теорема Ван Циттерта – Цернике предполагает, что среда между источником и плоскостью изображения однородна. Если среда неоднородна, то свет из одной области источника будет по-разному преломляться относительно других областей источника из-за разницы во времени прохождения света через среду. В случае неоднородной среды необходимо использовать обобщение теоремы Ван Циттерта–Цернике, называемое формулой Хопкинса.

Поскольку волновой фронт не проходит через идеально однородную среду, когда он проходит через межзвездную (и, возможно, межгалактическую ) среду и в атмосферу Земли , теорема Ван Циттерта-Цернике не совсем верна для астрономических источников. Однако на практике изменения показателя преломления межзвездной и межгалактической среды и атмосферы Земли достаточно малы, поэтому теорема приблизительно верна с точностью до любой разумной экспериментальной ошибки. Такие изменения показателя преломления среды приводят лишь к небольшим возмущениям, как в случае волнового фронта, проходящего через однородную среду.

Формула Хопкинса

Предположим, что мы имеем ситуацию, идентичную той, которая рассматривалась при выводе теоремы Ван Циттерта–Цернике, за исключением того, что среда теперь неоднородна. Поэтому мы вводим функцию пропускания среды: $K(l,m,P,\nu )$ . Следуя аналогичному выводу, как и раньше, мы находим, что

\Gamma _{12}(l,m,0)=\lambda ^{2}\iint I(l,m)K(l,m,P_{1},\nu )K^{*}(l,m,P_{2},\nu )\,dS

Если мы определим

U(l,m,P_{1})\equiv i\lambda K(l,m,P_{1},\nu ){\sqrt {I(l,m)}}

тогда функция взаимной когерентности принимает вид

\Gamma _{12}(l,m,0)=\iint U(l,m,P_{1})U^{*}(l,m,P_{2})\,dS

что является обобщением Хопкинса теоремы Ван Циттерта – Цернике. ^[8] В частном случае однородной среды функция пропускания принимает вид

K(l,m,P,\nu )=-{\frac {ie^{ikR}}{\lambda R}}

в этом случае функция взаимной когерентности сводится к преобразованию Фурье распределения яркости источника. Основное преимущество формулы Хопкинса состоит в том, что можно вычислить функцию взаимной когерентности источника косвенно, измеряя распределение его яркости.

Приложения теоремы

Синтез апертуры

Теорема Ван Циттерта – Цернике имеет решающее значение для измерения распределения яркости источника. С помощью двух телескопов радиоастроном (или инфракрасный или субмиллиметровый астроном) может измерить корреляцию между электрическим полем на двух антеннах из-за некоторой точки источника. Измеряя эту корреляцию для многих точек источника, астроном может восстановить функцию видимости источника. Применяя теорему Ван Циттерта-Цернике, астроном может затем воспользоваться обратным преобразованием Фурье функции видимости, чтобы обнаружить распределение яркости источника. Этот метод известен как синтез апертуры или синтез изображений.

На практике радиоастрономы редко восстанавливают распределение яркости источника путем прямого обратного преобразования Фурье измеренной функции видимости. Такой процесс потребует достаточного количества выборок, чтобы удовлетворить теореме выборки Найквиста ; это гораздо больше наблюдений, чем необходимо для приблизительного восстановления распределения яркости источника. Поэтому астрономы используют физические ограничения на распределение яркости астрономических источников, чтобы уменьшить количество наблюдений, которые необходимо провести. Поскольку распределение яркости должно быть реальным и положительным повсюду, функция видимости не может принимать произвольные значения в регионах без выборки. Таким образом, алгоритм нелинейной деконволюции, такой как CLEAN или Maximum Entropy, может использоваться для приблизительного восстановления распределения яркости источника на основе ограниченного числа наблюдений. ^[9]

Адаптивная оптика

Теорема Ван Циттерта – Цернике также накладывает ограничения на чувствительность системы адаптивной оптики . В системе адаптивной оптики (АО) обеспечивается искаженный волновой фронт, который необходимо преобразовать в волновой фронт без искажений. Система АО должна внести ряд различных поправок, чтобы устранить искажения волнового фронта. Одна из таких коррекций включает разделение волнового фронта на два одинаковых волновых фронта и смещение одного на некоторое физическое расстояние. $s$ в плоскости волнового фронта. Затем два волновых фронта накладываются, создавая узор полос. Измеряя размер и расстояние между полосами, система АО может определять разности фаз вдоль волнового фронта. ^[10] Этот метод известен как «стрижка».

Чувствительность этого метода ограничена теоремой Ван Циттерта – Цернике. ^[11] Если изображается протяженный источник, контраст между полосами будет уменьшен в раз, пропорциональном преобразованию Фурье распределения яркости источника. ^[12] Теорема Ван Циттерта-Цернике подразумевает, что взаимная когерентность протяженного источника, отображаемого системой АО, будет преобразованием Фурье его распределения яркости. Таким образом, расширенный источник изменит взаимную когерентность полос, уменьшив их контраст.

Лазер на свободных электронах

Теорему Ван Циттерта-Цернике можно использовать для расчета частичной пространственной когерентности излучения лазера на свободных электронах .

См. также

Ссылки

^ Леонард Мандель; Эмиль Вольф (1995). Оптическая когерентность и квантовая оптика (иллюстрировано, переиздано под ред.). Издательство Кембриджского университета. п. 188. ИСБН 978-0-521-41711-2 . Выдержка со страницы 188
^ Джеффри Брукер (2003). Современная классическая оптика (иллюстрировано, переиздано под ред.). ОУП Оксфорд. п. 227. ИСБН 978-0-19-859965-4 . Выдержка со страницы 227
^ Эл Джей Чоу (2009). Наноразмерные одномерные электронные и фотонные устройства 3 (NODEPD 3) (иллюстрированное издание). Электрохимическое общество. п. 16. ISBN 978-1-56677-747-6 . Выдержка со страницы 16
^ Томпсон, Арканзас; Моран, Дж. М.; Свенсон, GW (2017). Теорема Ван Циттерта–Цернике, пространственная когерентность и рассеяние. В кн.: Интерферометрия и синтез в радиоастрономии. Библиотека астрономии и астрофизики . Спрингер, Чам. дои : 10.1007/978-3-319-44431-4_15 . ISBN 978-3-319-44431-4 .
^ П.Х. ван Циттерт (1934). «Вероятное распространение колебаний в плоскости, освещенной источником света непосредственно или с помощью линзы». Физика . 1 (1–6): 201–210. Бибкод : 1934Phy.....1..201В . дои : 10.1016/S0031-8914(34)90026-4 .
^ Ф. Цернике (1938). «Понятие степени когерентности и его применение к оптическим проблемам». Физика . 5 (8): 785–795. Бибкод : 1938Phy.....5..785Z . дои : 10.1016/S0031-8914(38)80203-2 .
^ Гудман, Джозеф В. (1985). Статистическая оптика . Джон Уайли \& Sons, Inc.
^ Борн и Вольф, Принципы оптики , стр. 510.
^ Берк и Грэм-Смит, Введение в радиоастрономию , стр. 92.
^ Ф. Роддье, Адаптивная оптика в астрономии , стр. 95.
^ Дж. Харди, Адаптивная оптика для астрономических телескопов , стр. 159.
^ Колиопулос, Appl. Опт , 19 , 1523 (1980)

Библиография

Борн, М. и Вольф, Э .: Принципы оптики , Pergamon Press, Оксфорд, 1987, стр. 510
Кляйн, Майлз В. и Фуртак, Томас Э .: Оптика , John Wiley & Sons, Нью-Йорк, 1986, 2-е издание, с. 544-545

Внешние ссылки

Лекция по теореме Ван Циттерта–Цернике с приложениями. Университет Беркли, проф. Дэвид Т. Эттвуд на YouTube (AST 210/EE 213, лекция 23)]

[1] Леонард Мандель; Эмиль Вольф (1995). Оптическая когерентность и квантовая оптика (иллюстрировано, переиздано под ред.). Издательство Кембриджского университета. п. 188. ИСБН 978-0-521-41711-2 . Выдержка со страницы 188

[2] Джеффри Брукер (2003). Современная классическая оптика (иллюстрировано, переиздано под ред.). ОУП Оксфорд. п. 227. ИСБН 978-0-19-859965-4 . Выдержка со страницы 227

[3] Эл Джей Чоу (2009). Наноразмерные одномерные электронные и фотонные устройства 3 (NODEPD 3) (иллюстрированное издание). Электрохимическое общество. п. 16. ISBN 978-1-56677-747-6 . Выдержка со страницы 16

[4] Томпсон, Арканзас; Моран, Дж. М.; Свенсон, GW (2017). Теорема Ван Циттерта–Цернике, пространственная когерентность и рассеяние. В кн.: Интерферометрия и синтез в радиоастрономии. Библиотека астрономии и астрофизики . Спрингер, Чам. дои : 10.1007/978-3-319-44431-4_15 . ISBN 978-3-319-44431-4 .

[vancittert-5] П.Х. ван Циттерт (1934). «Вероятное распространение колебаний в плоскости, освещенной источником света непосредственно или с помощью линзы». Физика . 1 (1–6): 201–210. Бибкод : 1934Phy.....1..201В . дои : 10.1016/S0031-8914(34)90026-4 .

[zernike-6] Ф. Цернике (1938). «Понятие степени когерентности и его применение к оптическим проблемам». Физика . 5 (8): 785–795. Бибкод : 1938Phy.....5..785Z . дои : 10.1016/S0031-8914(38)80203-2 .

[7] Гудман, Джозеф В. (1985). Статистическая оптика . Джон Уайли \& Sons, Inc.

[born-8] Борн и Вольф, Принципы оптики , стр. 510.

[burke-9] Берк и Грэм-Смит, Введение в радиоастрономию , стр. 92.

[roddier-10] Ф. Роддье, Адаптивная оптика в астрономии , стр. 95.

[hardy-11] Дж. Харди, Адаптивная оптика для астрономических телескопов , стр. 159.

[koliopoulos-12] Колиопулос, Appl. Опт , 19 , 1523 (1980)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]