85 способов завязать галстук

85 способов завязать галстук
Автор	Томас Финк и Юн Мао
Издатель	Четвертое сословие
Дата публикации	4 ноября 1999 г.
ISBN	1-84115-249-8
ОКЛК	59397523

«85 способов завязать галстук» — это книга Томаса Финка и Юн Мао об истории завязанного галстука , современного галстука и о том, как его завязывать. Он основан на двух математических статьях, опубликованных авторами в журнале Nature. ^[1] и Physica A, когда они были научными сотрудниками Кембриджского университета в Кавендишской лаборатории . ^[2] Авторы доказывают, что, если предположить, что и галстук, и его владелец имеют типичный размер, существует ровно 85 способов завязывания галстука с использованием традиционного метода обертывания широкого конца галстука вокруг узкого конца. Они описывают каждый из них и выделяют те, которые, по их мнению, являются исторически примечательными или эстетически привлекательными.

Он был опубликован издательством «Четвертая власть» 4 ноября 1999 года и впоследствии опубликован на девяти других языках.

Математика

Открытие всех возможных способов завязывания галстука зависит от математической формулировки процесса завязывания галстука. В своих статьях (технических) и книге (предназначенной для непрофессионала, за исключением приложения) авторы показывают, что узлы галстука эквивалентны постоянным случайным блужданиям по треугольной решетке с некоторыми ограничениями на то, как эти блуждания начинаются и конец. Таким образом, перечисление связующих узлов из n ходов эквивалентно перечислению обходов из n шагов. Наложение условий симметрии и баланса уменьшает 85 узлов до 13 эстетических.

Представление узла

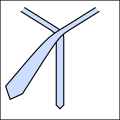
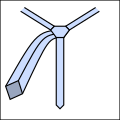
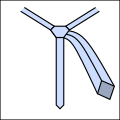
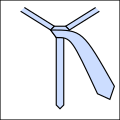
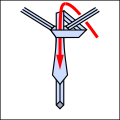
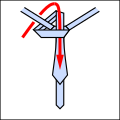
Основная идея заключается в том, что узлы галстука можно описать как последовательность пятиразличные возможные ходы, хотя не все ходы могут следовать друг за другом. Они резюмируются следующим образом. Все диаграммы выглядят так, как выглядел бы галстук, если бы вы носили его и смотрели в зеркало.

Л : слева; С : центр; Р : верно; они должны меняться при каждом движении.
я : в диаграмму; о : вне диаграммы; они должны чередоваться.
Т : через только что созданный цикл.

С помощью этого сокращения можно компактно выразить традиционные и новые узлы, как показано ниже. Обратите внимание, что любой узел, начинающийся с хода «о» , должен начинаться с вывернутого наизнанку галстука вокруг шеи. ^[3]

Примеры завязывания галстуков.
Ли начало.
Ло начало.
Это
Ро
Что
Ри
Ло Ри Ко Т конец.
Ро Ли Ко Т конец.

Узлы

Критерии выбора

Из 85 узлов, возможных для типичного галстука, Финк и Мао выбрали тринадцать как «эстетичные узлы», подходящие для использования. Свой выбор они сделали по трем критериям: форма, симметрия и баланс.

Форма

В классификации Финка и Мао каждый из 85 узлов связи принадлежит к определенному «классу», который определяется его общим количеством ходов и количеством центрирующих ходов. Например, «четверка» — это четырехходовой одноцентровый узел, а полувиндзор — шестиходовой двухцентровый узел. Узлы с меньшим количеством центрирующих движений (менее одной трети от общего количества) кажутся более узкими и вытянутыми, а узлы с большим количеством центрирующих движений кажутся более широкими и приземистыми. Из-за треугольной формы узлов связи количество центрирующих ходов обязательно должно быть меньше половины общего количества ходов.

Всего существует 16 классов, от трёх ходов с одним центром до девяти ходов с четырьмя центрами, но только классы, в которых соотношение центрирующих ходов к общему количеству ходов составляет 1:6 или больше, содержат эстетический узел, исключающий три класса ( десять узлов) для остальных 13 классов по 75 узлов. (В статье Nature нижняя граница была установлена на более строгом уровне 1:4, исключая классы узлов, содержащие узлы Кельвина, Виктории и Гранчестера; это, вероятно, было специально пересмотрено, чтобы включить узлы Виктория/Принц Альберт, которые довольно обширная историческая документация.) Затем на основе симметрии и баланса был выбран наиболее представительный узел в каждом оставшемся классе.

Симметрия

Симметрия в случае галстуковых узлов может относиться к двум возможным качествам: визуальной симметрии (степень, в которой узел кажется одинаковой формы с левой и правой стороны) и математической симметрией (количество движений L и R максимально близко чтобы быть максимально равным). Финк и Мао относятся к последнему, хотя некоторые узлы, которые слегка асимметричны (например, «Ники» и «Виндзор»), кажутся глазу симметричными. Математически симметричными могут быть только узлы с равным количеством общих ходов L и R, тогда как остальные эстетические узлы обязательно будут иметь на один больший ход L или R.

Баланс

Финк и Мао описывают баланс как «степень, в которой движения хорошо смешаны», называя его основным достоинством более тугой узел, который труднее развязывается. Он рассчитывается по определенной формуле, но непрофессионалу лучше всего может быть понят как степень, в которой движения L, R и C равномерно распределены по всей последовательности завязывания узлов, и степень, в которой узор LR или RL сохраняется непрерывно после нетерминальные центрирующие ходы (что требует смены направления намотки с против часовой стрелки на по часовой стрелке или наоборот). Эти качества проявляет каждый из эстетических узлов.

Ряд узлов имеет практически одинаковые варианты, отличающиеся перестановкой пар L и R. Например, вариант полувиндзора, Li Ro Ci Lo Ri Co T (узел 7), представляет собой узел Li Ro Ci Ro Li Co T (узел 8), иногда называемый полувиндзорским узлом. Упоминания о Полувиндзоре в литературе иногда относятся к одному, иногда к другому. Для целей книги, когда узел имеет хотя бы один вариант (т. е. когда два или более узлов с наибольшей степенью симметрии для своего класса имеют одну и ту же базовую структуру, за исключением одной или нескольких транспонированных пар LR), наиболее сбалансированной версии присвоено стандартное обозначение, а остальные помечены как варианты, независимо от таких качеств, как саморасстегивание (расстегивается при вытягивании узкого конца). Таким образом, более сбалансированному из двух «полувиндзорских» узлов присвоена меньшая нумерация и название «Полувиндзорский», хотя немного менее сбалансированный «полувиндзорский» вариант также известен как «Полувиндзорский». «Виндзор» в литературе о мужском стиле, и его преимущество заключается в том, что он саморазвязывается, а наиболее распространенный способ завязывания Виндзорского узла Финк и Мао называют «совиндзорский 3». Однако это не означает эстетического предпочтения одного варианта над другим; как отмечают авторы в своих журнальных статьях: «Мы не пытаемся отличить эти узлы от их аналогов; это мы оставляем на усмотрение читателя».

Три эстетических узла (Сент-Эндрю, Кавендиш и Гранчестер) имеют те же значения симметрии и баланса, что и по крайней мере еще один узел в их классе; в данном случае они, похоже, были выбраны на основе того, насколько равномерно они распределяют несбалансированные части по узлу. Это можно легко увидеть, если рассматривать эти узлы как комбинации двух меньших узлов, поскольку значения баланса каждого компонента складываются в значение баланса последнего узла. В несбалансированных узлах, где значение баланса нечетное, оно разбивается так, что более несбалансированная часть из двух помещается ближе к началу узла. Вероятно, это сделано для того, чтобы самая внешняя часть узла сохраняла свою форму и оставалась тугой.

13 эстетических узлов

Тринадцать эстетических узлов, описанных в книге (в порядке размера), следующие. Конечные последовательности (последние три хода, заканчивающиеся завязыванием узла) выделены жирным шрифтом. Узлы иногда обозначаются только их номером (например, FM2 для четверки в руке, а FM означает Финк-Мао). Узел считается саморазвязывающимся, если при вытягивании тонкого конца через узел узла не остается; поскольку все узлы начинаются слева, узел является саморазвязывающимся, если конечная последовательность равна Ro Li Co ; он не является самовысвобождающимся, если терминальная последовательность — Lo Ri Co. Симметрия и саморасцепление дополняют друг друга для узлов с наибольшей степенью сбалансированности для своего класса.

Число	Последовательность	Имя	Самовыпускающийся	Симметричный ^[4]
1.	Ло Ри Ко Т	Маленький узел	Нет	Да
2.	Ли Ро Ли Ко Т	Четверо в руке	Да	Нет
3.	Lo Ri Lo Ri Co T	Кельвин	Нет	Да
4.	Ло Си Ро Ли Ко Т	Ники	Да	Нет
6.	Ли Ро Ли Ро Ли Ко Т	Виктория	Да	Нет
7.	Ли Ро Си Ло Ри Ко Т	Половиндзор	Нет	Да
12.	Ло Ри Ло Си Ро Ли Ко Т	Святой Андрей	Да	Нет
18.	Ло Си Ро Си Ло Ри Ко Т	Платтсбург	Нет	Да
23.	Ли Ро Ли Ко Ри Ло Ри Ко Т	Кавендиш	Нет	Да
31.	Ли Ко Ри Ло Си Ро Ли Ко Т	Виндзор	Да	Нет
44.	Ло Ри Ло Ри Ко Ли Ро Ли Ко Т	Гранчестер	Да	Нет
54.	Ло Ри Ко Ли Ро Си Ло Ри Ко Т	Ганновер	Нет	Да
78.	Ло Си Ро Си Ло Си Ро Ли Ко Т	Бальтюс	Да	Нет

Три распространенных варианта узлов заключаются в следующем. Они включены из-за их общности (Пратт, полувиндзорский вариант) или из-за возможности самовысвобождения, в отличие от их более «эстетичных» аналогов (полувиндзорский вариант, ганноверский вариант). Варианты Half-Windsor и Hanover имеют то преимущество, что они симметричны и саморасстегиваются, но они менее сбалансированы, чем их аналоги выше:

Число	Последовательность	Имя	Самовыпускающийся	Симметричный ^[4]
5.	Ло Си Ло Ри Ко Т	Пратт	Нет	Нет
8.	Ли Ро Чи Ро Ли Ко Т	Полувиндзорский вариант	Да	Да
55.	Ло Ри Ко Ри Ло Си Ро Ли Ко Т	Ганноверский вариант	Да	Да

Отзывы

Рецензия на книгу была опубликована в журнале Nature . ^[5] The Daily Telegraph , The Guardian , GQ , Physics World и другие.

Ссылки

^ Финк, Томас М .; Юн Мао (1999). «Проектирование узлов галстука методом случайных блужданий» (PDF) . Природа . 398 (6722): 31–32. дои : 10.1038/17938 .
^ Финк, Томас М .; Юн Мао (2000). «Узлы связи, случайные блуждания и топология» (PDF) . Физика А. 276 (1–2): 109–121. дои : 10.1016/S0378-4371(99)00226-5 .
^ «Как завязать галстук – быстро и очень легко, шаг за шагом» . www.ezone57.net . 15 февраля 2023 г. Проверено 2 мая 2024 г.
^ Jump up to: ^а ^б Энциклопедия галстуковых узлов на домашней странице Томаса Финка
^ Бак, Грегори (2000). «Почему бы не завязать правильный узел?». Природа . 403 (6768): 362. дои : 10.1038/35000270 .

Внешние ссылки

Узлы для галстуков у Керли
Урок Джеффа Бэнкса « Как завязать галстук»

[1] Финк, Томас М .; Юн Мао (1999). «Проектирование узлов галстука методом случайных блужданий» (PDF) . Природа . 398 (6722): 31–32. дои : 10.1038/17938 .

[2] Финк, Томас М .; Юн Мао (2000). «Узлы связи, случайные блуждания и топология» (PDF) . Физика А. 276 (1–2): 109–121. дои : 10.1016/S0378-4371(99)00226-5 .

[3] «Как завязать галстук – быстро и очень легко, шаг за шагом» . www.ezone57.net . 15 февраля 2023 г. Проверено 2 мая 2024 г.

[fink-4] Jump up to: ^а ^б Энциклопедия галстуковых узлов на домашней странице Томаса Финка

[5] Бак, Грегори (2000). «Почему бы не завязать правильный узел?». Природа . 403 (6768): 362. дои : 10.1038/35000270 .

[1]

[2]

[3]

[4]

[5]

v т и Узел галстука
Necktie knots	Four-in-hand knot (simple or schoolboy) Grantchester knot Half-Windsor knot Pratt knot (Shelby) Small knot (Oriental or Kent) Windsor knot (full Windsor)
See also	The 85 Ways to Tie a Tie