График МакГи
| График МакГи | |
|---|---|
 График МакГи | |
| Назван в честь | ВФ МакГи |
| Вершины | 24 |
| Края | 36 |
| Радиус | 4 |
| Диаметр | 4 [1] |
| Обхват | 7 [1] |
| Автоморфизмы | 32 [1] |
| Хроматическое число | 3 [1] |
| Хроматический индекс | 3 [1] |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Кубический Клетка гамильтониан |
| Таблица графиков и параметров | |
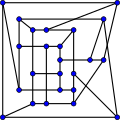
В математической области теории графов граф МакГи или (3-7)-клетка представляет собой 3- регулярный граф с 24 вершинами и 36 ребрами. [1]
Граф МакГи представляет собой уникальную (3,7) -клетку (наименьший кубический граф обхвата 7). Это также наименьшая кубическая клетка, не являющаяся графом Мура .
Впервые обнаружен Саксом, но не опубликован. [2] график назван в честь Макги, опубликовавшего результат в 1960 году. [3] Затем в 1966 году Тутте доказал, что граф МакГи является уникальной (3,7)-клеткой. [4] [5] [6]
Граф МакГи требует не менее восьми пересечений на любом его изображении на плоскости. Это один из трех неизоморфных графов, связанных с тем, что он является наименьшим кубическим графом, требующим восьми пересечений. Еще один из этих трех графов — обобщенный граф Петерсена G (12,5) , также известный как граф Науру . [7] [8]
Граф МакГи имеет радиус 4, диаметр 4, хроматическое число 3 и хроматический индекс 3. Это также 3 -связный граф и 3 -связный граф. Имеет толщину книги 3 и номер очереди 2. [9]
Алгебраические свойства
[ редактировать ]Характеристический полином графа МакГи равен
- .
Группа автоморфизмов графа МакГи имеет порядок 32 и не действует транзитивно на своих вершинах: существует две орбиты вершин длиной 8 и 16. Граф МакГи — это наименьшая кубическая клетка, которая не является вершинно-транзитивным графом . [10]
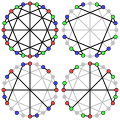
Галерея
[ редактировать ]- Число пересечений графа МакГи равно 8.
- Хроматическое число графа МакГи равно 3.
- Хроматический индекс графа МакГи равен 3.
- Ациклическое хроматическое число графа МакГи равно 3.
- Альтернативный рисунок графа МакГи.
Ссылки
[ редактировать ]- ^ Jump up to: а б с д и ж Вайсштейн, Эрик В. «График МакГи» . Математический мир .
- ^ Картези, Ф. «Циклические конечные плоскости как решение определенной задачи минимизации». Бык. Мэтт. Итал. 15, 522–528, 1960 г.
- ^ МакГи, WF (1960). «Минимальный кубический граф обхвата семь» . Канадский математический бюллетень . 3 (2): 149–152. дои : 10.4153/CMB-1960-018-1 .
- ^ Тутте, Связь WT в графиках. Торонто, Онтарио: University of Toronto Press, 1966.
- ^ Вонг, Пак-Кен (1982). «Клетки — Исследование». Журнал теории графов . 6 : 1–22. дои : 10.1002/jgt.3190060103 .
- ^ Брауэр, А.Э.; Коэн, AM; и Ноймайер А. Дистанционные регулярные графы. Нью-Йорк: Springer-Verlag, с. 209, 1989 г.
- ^ Слоан, Нью-Джерси (ред.). «Последовательность A110507 (Количество узлов в наименьшем кубическом графе с номером пересечения n)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.
- ^ Пегг, ET ; Эксу, Г. (2009). «Пересечение числовых графиков» . Журнал Математика . 11 (2). дои : 10.3888/tmj.11.2-2 . .
- ^ Джессика Вольц, Разработка линейных макетов с помощью SAT . Магистерская диссертация, Тюбингенский университет, 2018 г.
- ^ Жайкай, Роберт; Ширань, Йозеф (2011). «Малые вершинно-транзитивные графы заданной степени и обхвата». Ars Mathematica Contemporanea . 4 (2): 375–384. дои : 10.26493/1855-3974.124.06d .