Управляемость сети

сети касается структурной управляемости сети Управляемость . Управляемость описывает нашу способность направлять динамическую систему из любого начального состояния в любое желаемое конечное состояние за конечное время с подходящим выбором входных данных. Это определение хорошо согласуется с нашим интуитивным представлением о контроле. Управляемость общенаправленных и взвешенных сложных сетей в последнее время стала предметом интенсивного изучения рядом групп, работающих в самых разных сетях по всему миру. Недавние исследования Sharma et al. [1] на мультитипических биологических сетях (сети ген-ген, микроРНК-ген и белок-белковое взаимодействие) идентифицировали контрольные мишени при фенотипически охарактеризованной остеосаркоме, показывая важную роль генов и белков, ответственных за поддержание микроокружения опухоли.
Предыстория [ править ]
Рассмотрим каноническую линейную нестационарную динамику в сложной сети где вектор фиксирует состояние системы узлы во времени . матрица описывает схему подключения системы и силу взаимодействия между компонентами. матрица идентифицирует узлы, управляемые внешним контроллером. Система управляется через зависящий от времени входной вектор. которые контроллер налагает на систему. Чтобы определить минимальное количество узлов драйвера, обозначаемое , чей контроль достаточен для полного контроля динамики системы, Лю и др. [2] попытался объединить инструменты теории структурного управления, теории графов и статистической физики. Они показали [2] что минимальное количество входов или узлов драйверов, необходимое для поддержания полного контроля над сетью, определяется соответствием максимальной мощности в сети. На основе этого результата была разработана аналитическая основа, основанная на распределении степеней «вход-выход» для прогнозирования. для безмасштабных и случайных графов Эрдеша–Реньи . [2] Однако совсем недавно было продемонстрировано, что управляемость сети (и другие методы, основанные только на структуре, которые используют исключительно связность графа, , чтобы упростить основную динамику), как недостигать, так и превышать количество, а также какие наборы узлов драйвера лучше всего контролируют динамику сети, подчеркивая важность избыточности (например, канализации) и нелинейной динамики при определении управления. [3]
Также примечательно, что Liu's et al. формулировка [2] предсказал бы те же значения для цепного графа и для слабого плотносвязного графа. Очевидно, что оба этих графика имеют очень разные распределения степеней. Недавняя неопубликованная работа [4] возникает вопрос, будет ли степень , которая является чисто локальной мерой в сетях, полностью описывать управляемость и будут ли даже немного удаленные узлы не играть никакой роли в определении управляемости сети. Действительно, для многих реальных сетей, а именно пищевых сетей, нейронных и метаболических сетей, несоответствие значений и рассчитано Лю и др. [2] примечательно. Если управляемость определяется главным образом степенью, то почему и настолько разные для многих реальных сетей? Они спорили [2] (arXiv:1203.5161v1), что это может быть связано с эффектом корреляции степеней. Однако было показано [4] что управляемость сети можно изменить, только используя центральность по посредничеству и центральность по близости , без использования степени (теории графов) вообще или корреляций степеней.
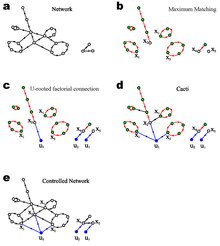
управляемость Структурная
Понятие структурных свойств было впервые введено Лином (1974). [5] а затем расширен Шилдсом и Пирсоном (1976). [6] и, альтернативно, получено Гловером и Сильверманом (1976). [7] Главный вопрос заключается в том, является ли отсутствие управляемости или наблюдаемости характерным для переменных параметров системы. В рамках структурного управления параметрами системы являются либо независимые свободные переменные, либо фиксированные нули. Это справедливо для моделей физических систем, поскольку значения параметров никогда не известны точно, за исключением нулевых значений, которые выражают отсутствие взаимодействий или связей.
Максимальное соответствие [ править ]
В теории графов паросочетание — это набор ребер, не имеющих общих вершин. Лю и др. [2] распространил это определение на ориентированный граф, где паросочетание представляет собой набор направленных ребер, которые не имеют общих начальных или конечных вершин. Легко проверить, что паросочетание ориентированного графа представляет собой набор вершинно-непересекающихся простых путей и циклов. Максимальное сопоставление направленной сети можно эффективно вычислить, работая в двудольном представлении с использованием классического алгоритма Хопкрофта – Карпа выполняется за время O( E √ N , который в худшем случае ). Для неориентированного графа аналитические решения размера и количества максимальных паросочетаний были изучены с использованием метода полости, разработанного в статистической физике. [8] Лю и др. [2] расширил вычисления для ориентированного графа.
Рассчитывая максимальные совпадения широкого спектра реальных сетей, Лю и др. [2] утверждал, что количество узлов-драйверов определяется главным образом распределением степени сети . Они также рассчитали среднее количество узлов-драйверов для ансамбля сети с произвольным распределением степеней, используя метод полости . Интересно, что для цепного графа и слабого плотносвязного графа, оба из которых имеют очень разные распределения степеней по входу и выходу; формулировка Liu et al. [2] предсказал бы те же значения . Кроме того, для многих сетей реального мира, а именно пищевых сетей, нейронных и метаболических сетей, несоответствие значений и рассчитано Лю и др. [2] примечательно. Если управляемость определяется исключительно степенью, то почему и настолько разные для многих реальных сетей? Остается открытым вопрос о том, влияет ли «устойчивость управления» в сетях в большей степени при использовании централизации по промежуточности и централизации по близости. [4] над метриками, основанными на степени .
Хотя более разреженные графики труднее контролировать, [2] [4] очевидно, было бы интересно выяснить, являются ли центральность по посредничеству и центральность по близости [4] или степень неоднородности [2] играет более важную роль в определении управляемости разреженных графов с почти подобными распределениями степеней.
составными квантовыми системами и алгебраическая теория Управление графов
Теория управления сетями также была разработана в контексте универсального управления составными квантовыми системами, где подсистемы и их взаимодействия связаны с узлами и связями соответственно. [9] Эта структура позволяет сформулировать критерий Калмана с помощью инструментов алгебраической теории графов через минимальный ранг графа и связанные с ним понятия. [10] [11]
См. также [ править ]
Ссылки [ править ]
- ^ Шарма, Анкуш; Чинти, Катерина; Капобьянко, Энрико (2017). «Многотиповая сетевая целевая управляемость при фенотипически охарактеризованной остеосаркоме: роль микроокружения опухоли» . Границы в иммунологии . 8 : 918. дои : 10.3389/fimmu.2017.00918 . ISSN 1664-3224 . ПМЦ 5536125 . ПМИД 28824643 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час я дж к л м Лю, Ян-Ю; Слотин, Жан-Жак; Барабаши, Альберт-Ласло (2011). «Управляемость сложных сетей». Природа . 473 (7346). ООО «Спрингер Сайенс энд Бизнес Медиа»: 167–173. Бибкод : 2011Natur.473..167L . дои : 10.1038/nature10011 . ISSN 0028-0836 . ПМИД 21562557 . S2CID 4334171 .
- ^ Гейтс, Александр Дж.; Роша, Луис М. (18 апреля 2016 г.). «Управление сложными сетями требует как структуры, так и динамики» . Научные отчеты . 6 (1). Springer Science and Business Media LLC: 24456. arXiv : 1509.08409 . Бибкод : 2016НатСР...624456Г . дои : 10.1038/srep24456 . ISSN 2045-2322 . ПМЦ 4834509 . ПМИД 27087469 .
- ^ Jump up to: Перейти обратно: а б с д и Банерджи, С.Дж.; Рой, С. (2012). «Ключ к управляемости сети». arXiv : 1209.3737 [ physical.soc-ph ].
- ^ Jump up to: Перейти обратно: а б К.-Т. Лин, IEEE Trans. Авто. Контр. 19 (1974).
- ^ Р.В. Шилдс и Дж.Б. Пирсон, IEEE Trans. Авто. Контр. 21 (1976).
- ^ К. Гловер и Л. М. Сильверман, IEEE Trans. Авто. Контр. 21 (1976).
- ^ Л. Здеборова и М. Мезар, J. Stat. Мох. 05 (2006).
- ^ Бургарт, Дэниел; Джованнетти, Витторио (5 сентября 2007 г.). «Полный контроль посредством локально-индуцированной релаксации». Письма о физических отзывах . 99 (10): 100501. arXiv : 0704.3027 . Бибкод : 2007PhRvL..99j0501B . дои : 10.1103/physrevlett.99.100501 . ISSN 0031-9007 . ПМИД 17930379 . S2CID 6560929 .
- ^ Бургарт, Дэниел; Д'Алессандро, Доменико; Хогбен, Лесли ; Северини, Симона; Янг, Майкл (2013). «Нулевое принуждение, линейная и квантовая управляемость для систем, развивающихся в сетях» . Транзакции IEEE при автоматическом управлении . 58 (9): 2349–2354. arXiv : 1111.1475 . дои : 10.1109/TAC.2013.2250075 . МР 3101617 . S2CID 6939245 .
- ^ С. О'Рурк, Б. Тури, https://arxiv.org/abs/1511.05080. Архивировано 18 октября 2016 г. в Wayback Machine .














