Самая длинная общая подстрока

Не путать с самой длинной общей подпоследовательностью .

В информатике самая длинная общая подстрока из двух или более строк — это самая длинная строка , которая является подстрокой всех из них. Может существовать более одной самой длинной общей подстроки. Приложения включают дедупликацию данных и обнаружение плагиата .

Примеры

Строки «BADANAT» и «CANADAS» имеют общие подстроки «ADA» и «ANA» максимальной длины.

На рисунке показаны две строки, где задача имеет несколько решений. Хотя вхождения подстроки всегда перекрываются, невозможно получить более длинную общую подстроку, «объединив» их.

Строки «ABABC», «BABCA» и «ABCBA» имеют только одну самую длинную общую подстроку, а именно. «ABC» длиной 3. Другими распространенными подстроками являются «A», «AB», «B», «BA», «BC» и «C».

  ABABC
    |||
   BABCA
    |||
    ABCBA

Определение проблемы

Учитывая две строки, $S$ длины $m$ и $T$ длины $n$, найдите самую длинную строку, которая является подстрокой обеих $S$ и $T$.

Обобщением является задача о k - общих подстроках . Учитывая набор строк $S=\{S_{1},\ldots ,S_{K}\}$, где $|S_{i}|=n_{i}$ и ${\textstyle \sum n_{i}=N}$. Найдите для каждого $2\leq k\leq K$, самая длинная строка, которая встречается как подстрока как минимум $k$ струны.

Алгоритмы

Можно найти длины и начальные позиции самых длинных общих подстрок $S$ и $T$ в $\Theta$$(n+m)$ время с помощью обобщенного суффиксного дерева . Более быстрый алгоритм может быть достигнут в модели вычислений со словным ОЗУ , если размер $\sigma$ входного алфавита находится в $2^{o\left({\sqrt {\log(n+m)}}\right)}$. В частности, этот алгоритм работает в ${\textstyle O\left((n+m)\log \sigma /{\sqrt {\log(n+m)}}\right)}$ время использования $O\left((n+m)\log \sigma /\log(n+m)\right)$ космос. Решение проблемы за счет на динамическое программирование затрат $\Theta (nm)$. Решение обобщенной задачи принимает $\Theta (n_{1}+\cdots +n_{K})$ пространство и $\Theta (n_{1}\cdots n_{K})$ время с динамическим программированием и принять $\Theta (n_{1}+\cdots +n_{K})$ время с обобщенным суффиксным деревом .

Суффиксное дерево

Обобщенное суффиксное дерево для строк «ABAB», «BABA» и «ABBA» с номерами 0, 1 и 2.

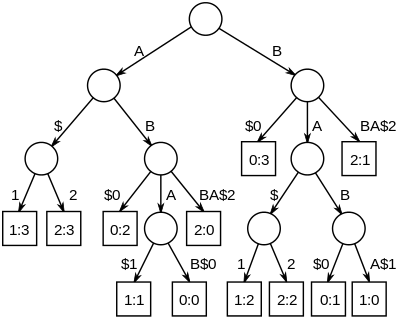
Самые длинные общие подстроки набора строк можно найти, построив обобщенное суффиксное дерево для строк, а затем найдя самые глубокие внутренние узлы, имеющие конечные узлы из всех строк в поддереве ниже него. Рисунок справа представляет собой суффиксное дерево строк «ABAB», «BABA» и «ABBA», дополненное уникальными символами завершения строки, чтобы превратиться в «ABAB$0», «BABA$1» и «ABBA$2». Узлы, представляющие «A», «B», «AB» и «BA», имеют листья-потомки всех строк с номерами 0, 1 и 2.

Построение суффиксного дерева занимает $\Theta (N)$ время (если размер алфавита постоянный). Если дерево обходится снизу вверх с помощью битового вектора, указывающего, какие строки находятся под каждым узлом, проблема k-общих подстрок может быть решена в $\Theta (NK)$ время. Если суффиксное дерево подготовлено для поиска наименьшего общего предка за постоянное время , его можно решить в $\Theta (N)$ время.

Динамическое программирование

Следующий псевдокод находит набор самых длинных общих подстрок между двумя строками с помощью динамического программирования:

function LongestCommonSubstring(S[1..r], T[1..n])
    L := array(1..r, 1..n)
    z := 0
    ret := {}

    for i := 1..r
        for j := 1..n
            if S[i] = T[j]
                if i = 1 or j = 1
                    L[i, j] := 1
                else
                    L[i, j] := L[i − 1, j − 1] + 1
                if L[i, j] > z
                    z := L[i, j]
                    ret := {S[i − z + 1..i]}
                else if L[i, j] = z
                    ret := ret ∪ {S[i − z + 1..i]}
            else
                L[i, j] := 0
    return ret

Этот алгоритм работает в $O(nr)$ время. Массив L хранит длину самой длинной общей подстроки префиксов S[1..i] и T[1..j] которые заканчиваются на позиции i и j, соответственно. Переменная z используется для хранения длины самой длинной общей подстроки, найденной на данный момент. Набор ret используется для хранения набора строк длиной z. Набор ret можно эффективно сохранить, просто сохранив индекс i, который является последним символом самой длинной общей подстроки (размера z) вместо S[i-z+1..i]. Таким образом, все самые длинные общие подстроки будут для каждого i в ret, S[(ret[i]-z)..(ret[i])].

Следующие приемы можно использовать для уменьшения использования памяти реализацией:

• Для экономии памяти оставьте только последнюю и текущую строку таблицы DP ( $O(\min(r,n))$ вместо $O(nr)$)
  • Последняя и текущая строки могут быть сохранены в одном и том же одномерном массиве, пройдя внутренний цикл назад.
• Сохраняйте в строках только ненулевые значения. Это можно сделать, используя хеш-таблицы вместо массивов. Это полезно для больших алфавитов.

См. также

• Самая длинная палиндромная подстрока
• n -gram , все возможные подстроки длины n , содержащиеся в строке

Внешние ссылки

• Словарь алгоритмов и структур данных: самая длинная общая подстрока
• Perl/XS реализация алгоритма динамического программирования
• Perl/XS реализация алгоритма суффиксного дерева
• Реализации динамического программирования на разных языках в викибуках
• рабочая реализация AS3 алгоритма динамического программирования
• Реализация C на основе суффиксного дерева самой длинной общей подстроки для двух строк