Суперпермейт

В комбинаторной математике суперперммутация строка на n символах - это , которая содержит каждую перестановку -символов N в качестве подстроения . Хотя тривиальные суперперматации могут быть просто составлены из каждой перестановки, объединенной вместе, суперматации также могут быть короче (за исключением тривиального случая n = 1), поскольку разрешено перекрытие. Например, в случае n = 2 Superpermutation 1221 содержит все возможные перестановки (12 и 21), но более короткая строка 121 также содержит оба перестановки.

Было показано, что для 1 ≤ n ≤ 5 наименьшее суперперммутация на N -символах имеет длину 1! + 2! +… + N ! (последовательность A180632 в OEI ). Первые четыре наименьших суперперматации имеют соответствующие длины 1, 3, 9 и 33, образующие струны 1, 121, 123121321 и 123412314231243121342132413214321. Однако для n = 5, есть несколько самых маленьких суперперматации, имеют длину 153. Один из таких суперперматаций. показано ниже, в то время как еще одна и та же длина может быть полученным путем переключения всех четырех и пятерки во второй половине струны (после жирного шрифта 2 ): ^{[ 1 ]}

1234512341523412534123541231452314253142351423154231245312435124315243125431 2 1345213425134215342135421324513241532413524132541321453214352143251432154321

Для случаев n > 5 наименьшая суперперммутация еще не была доказана, ни схема, чтобы найти их, но были найдены нижние и верхние границы для них.

Поиск суперперматации

Диаграмма создания суперперммутации с 3 символами из суперпермутации с двумя символами

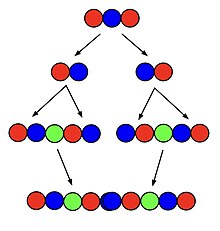
Один из наиболее распространенных алгоритмов для создания суперперматации порядка $n$ это рекурсивный алгоритм. Во -первых, суперпермутация порядка $n-1$ разделен на свои индивидуальные перестановки в порядке того, как они появились в суперпермутации. Затем каждая из этих перестановки помещается рядом с собственной копией с помощью N -TH -символа, добавленного между двумя копиями. Наконец, каждая полученная структура расположена рядом друг с другом, и все соседние идентичные символы объединяются. ^{[ 2 ]}

Например, суперпермутация Ордена 3 может быть создана из одного с двумя символами; Начиная с суперпермутации 121 и разделяя его на перестановки 12 и 21, перестановки копируются и размещаются как 12312 и 21321. Они расположены вместе для создания 123121321, а идентичные соседние 2 с в середине объединяются для создания 12312131, который идентичные соседние 2 с в середине объединяются для создания 123121321, которые идентичные соседние 2 с. действительно является суперпермутацией порядка 3. Этот алгоритм приводит к кратчайшей супермеротации для всех n меньше, чем или равен 5, но становится все более длинным, чем максимально кратчайшим, как n увеличивается за пределы этого. ^{[ 2 ]}

Другим способом поиска суперперматации заключается в создании графика , где каждая перестановка является вершиной , и каждая перестановка связана с краем. Каждый край имеет вес, связанный с ним; Вес рассчитывается, увидев, сколько символов может быть добавлено до конца одной перестановки (сбросив одно и то же количество символов с самого начала), чтобы привести к другой перестановке. ^{[ 2 ]} Например, преимущество от 123 до 312 имеет вес 2, потому что 123 + 12 = 12312 = 312. Любой гамильтонианский путь через созданный график является суперперммутацией, и проблема поиска пути с наименьшим весом становится формой путешествующего продавца проблема . Первый случай суперперммутации меньше длины $1!+2!+\ldots +n!$ был найден с использованием компьютерного поиска по этому методу Робином Хьюстоном.

Нижние границы или проблема харухи

анонимный плакат о по науке и математике (" / sci / ") совете 4chan В сентябре 2011 года доказал, что наименьшая суперперммута на n символах ( n ≥ 2) имеет по крайней мере длину n ! + ( n -1)! + ( n −2)! + n - 3. ^{[ 3 ]} Что касается японской аниме -серии «Меланхолия Харухи Сузумия» , особенно тот факт, что она первоначально транслировалась как нелинейное повествование , проблема была представлена на доске изображений как «проблема харухи»: ^{[ 4 ]} Если бы вы хотели посмотреть 14 эпизодов первого сезона сериала в каждом возможном порядке, что будет самой короткой цепочкой эпизодов, которые вам нужно будет посмотреть? ^{[ 5 ]} Доказательство этой нижней границы пришло к широкому общественному интересам в октябре 2018 года, после того, как математик и компьютерный ученый Робин Хьюстон написал об этом. ^{[ 3 ]} 25 октября 2018 года Робин Хьюстон, Джей Пантоне и Винс Вартер опубликовали утонченную версию этого доказательства в онлайн-энциклопедии целочисленных последовательностей (OEI). ^{[ 5 ]}^{[ 6 ]} Опубликованная версия этого доказательства, приписанная «анонимному 4ч -плакату», появляется в Engen and Vatter ( 2021 ). ^{[ 7 ]} В частности, для «проблемы харухи (случай для 14 символов) текущая нижняя и верхняя граница составляет 93 884,313,611 и 93 924 230,411 соответственно. ^{[ 3 ]} Это означает, что просмотр сериала в каждом возможном порядке потребует около 4,3 миллионов лет. ^{[ 8 ]}

Верхние границы

20 октября 2018 года, адаптируя строительство Аарона Уильямса для строительства гамильтонианских путей через график Cayley группы симметричной , ^{[ 9 ]} Автор научной фантастики и математик Грег Иган разработал алгоритм для производства суперперматации длины n ! + ( n -1)! + ( n −2)! + ( n −3)! + n - 3. ^{[ 2 ]} До 2018 года это были самые маленькие суперперматации ≥ 7 . n известные , ( n ! ) -2 + ^{[ 2 ]} 27 февраля 2019 года, используя идеи, разработанные Робином Хьюстоном, Иган создал суперпермутацию для n = 7 из длины 5906. ^{[ 2 ]} Существуют ли аналогичные более короткие суперперматации для значений n > 7, остается открытым вопросом. Лучшая нижняя граница тока (см. Раздел выше) для n = 7 по -прежнему 5884.

Смотрите также

Superpattern , перестановка, которая содержит каждую перестановку N -символов как шаблон перестановки
Последовательность de bruijn , похожая проблема с циклическими последовательностями

Дальнейшее чтение

Эшлок, Даниэль А.; Tillotson, Jenett (1993), «Строительство небольших суперперматаций и минимальных инъективных суперстраций», Congressum Numerantium , 93 : 91–98, ZBL 0801.05004
Анонимный 4ч -плакат; Хьюстон, Робин; Пантоне, Джей; Вестер, Винс (25 октября 2018 г.). «Нижняя граница по длине самого короткого сверхпаттерна» (PDF) . Онлайн-энциклопедия целочисленных последовательностей . {{cite journal}}: CS1 Maint: числовые имена: список авторов ( ссылка )

Ссылки

^ Джонстон, Натаниэль (28 июля 2013 г.). «Неограниченность минимальных суперперматаций» . Дискретная математика . 313 (14): 1553–1557. Arxiv : 1303.4150 . BIBCODE : 2013ARXIV1303.4150J . doi : 10.1016/j.disc.2013.03.024 . S2CID 12018639 . ZBL 1368.05004 . Получено 16 марта 2014 года .
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон Иган, Грег (20 октября 2018 г.). «Суперперматации» . gregegan.net . Получено 15 января 2020 года .
^ Jump up to: ^а ^{беременный} ^в Григгс, Мэри Бет. «Анонимный пост 4chan может помочь решить 25-летнюю математическую тайну» . Грава .
^ Anon, - SAN (17 сентября 2011 г.). III "Перетуттационная нить III Норос
^ Jump up to: ^а ^{беременный} Кларрейх, Эрика (5 ноября 2018 г.). «Научно-фантастический писатель Грег Иган и анонимная проблема Math Whiz Advance Mumbure» . Quanta Magazine . Получено 21 июня 2020 года .
^ Анонимный 4ч -плакат; Хьюстон, Робин; Пантоне, Джей; Вестер, Винс (25 октября 2018 г.). «Нижняя граница по длине самого короткого сверхпаттерна» (PDF) . OEIS . Получено 27 октября 2018 года . {{cite web}}: CS1 Maint: числовые имена: список авторов ( ссылка )
^ Энген, Майкл; Vatter, Винсент (2021), «содержащий все перестановки», американский математический месяц , 128 (1): 4–24, Arxiv : 1810.08252 , doi : 10.1080/00029890.2021.1835384
^ Spalding, Katie (2018-10-30). «4chan только что решил многолетнюю математическую тайну» . IflScience . Получено 2023-10-05 .
^ Аарон, Уильямс (2013). «Гамильтоничность Cayley Digraph в симметричной группе, сгенерированной σ = (1 2 ... N) и τ = (1 2)». arxiv : 1307.2549v3 [ math.co ].

Внешние ссылки

Минимальная проблема суперпермутации - блог Натаниэля Джонстона
Грама, Джеймс. "Supermutations - NumberPhile" (видео) . YouTube . Брэди Харан . Получено 1 февраля 2018 года .
Оригинальный пост 4chan на / sci / , архивировано на varosu.org
Твит Робин Хьюстон, который привлек внимание 4чан
Статья о проблеме поиска коротких суперперматаций в журнале Quanta

[1] Джонстон, Натаниэль (28 июля 2013 г.). «Неограниченность минимальных суперперматаций» . Дискретная математика . 313 (14): 1553–1557. Arxiv : 1303.4150 . BIBCODE : 2013ARXIV1303.4150J . doi : 10.1016/j.disc.2013.03.024 . S2CID 12018639 . ZBL 1368.05004 . Получено 16 марта 2014 года .

[Greg_Egan-2] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон Иган, Грег (20 октября 2018 г.). «Суперперматации» . gregegan.net . Получено 15 января 2020 года .

[:0-3] Jump up to: ^а ^{беременный} ^в Григгс, Мэри Бет. «Анонимный пост 4chan может помочь решить 25-летнюю математическую тайну» . Грава .

[4] Anon, - SAN (17 сентября 2011 г.). III "Перетуттационная нить III Норос

[:1-5] Jump up to: ^а ^{беременный} Кларрейх, Эрика (5 ноября 2018 г.). «Научно-фантастический писатель Грег Иган и анонимная проблема Math Whiz Advance Mumbure» . Quanta Magazine . Получено 21 июня 2020 года .

[6] Анонимный 4ч -плакат; Хьюстон, Робин; Пантоне, Джей; Вестер, Винс (25 октября 2018 г.). «Нижняя граница по длине самого короткого сверхпаттерна» (PDF) . OEIS . Получено 27 октября 2018 года . {{cite web}}: CS1 Maint: числовые имена: список авторов ( ссылка )

[engenvatter-7] Энген, Майкл; Vatter, Винсент (2021), «содержащий все перестановки», американский математический месяц , 128 (1): 4–24, Arxiv : 1810.08252 , doi : 10.1080/00029890.2021.1835384

[8] Spalding, Katie (2018-10-30). «4chan только что решил многолетнюю математическую тайну» . IflScience . Получено 2023-10-05 .

[9] Аарон, Уильямс (2013). «Гамильтоничность Cayley Digraph в симметричной группе, сгенерированной σ = (1 2 ... N) и τ = (1 2)». arxiv : 1307.2549v3 [ math.co ].

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]