Теорема перечисления Полиа

Теорема перечисления Пойа , также известная как теорема Редфилда-Пойа и подсчет Полиа , — это теорема в комбинаторике , которая одновременно следует из леммы Бернсайда о количестве орбит на действия группы множестве и в конечном итоге обобщает ее . Теорема была впервые опубликована Дж. Ховардом Редфилдом в 1927 году. В 1937 году она была независимо переоткрыта Джорджем Полиа , который затем широко популяризировал результат, применив его ко многим задачам счета, в частности к подсчету химических соединений .

Теорема нумерации Пойа была включена в символическую комбинаторику и теорию комбинаторных видов .

Упрощенная, невзвешенная версия

Пусть X — конечное множество пусть G — группа перестановок действующая X и (или конечная группа симметрии, на X , ) . Набор X может представлять собой конечный набор бусинок, а G может быть выбранной группой перестановок бусинок. Например, если X — ожерелье из n бусинок в круге, то вращательная симметрия важна , поэтому G — циклическая группа Cn _, а если X — браслет из n бусинок в круге, вращения и отражения важны G , поэтому группа диэдра D _n порядка 2 n . Предположим далее, что Y — конечное множество цветов — цветов бус — так что Y ^Х — это набор цветных композиций из бусин (более формально: Y ^Х это набор функций $X\to Y$ .) Тогда группа G действует на Y ^Х. Теорема нумерации Пойа подсчитывает количество орбит под G цветных наборов бусин по следующей формуле:

\left|Y^{X}/G\right|={\frac {1}{|G|}}\sum _{g\in G}m^{c(g)}

где $m=|Y|$ — количество цветов, а c ( g ) — количество циклов группового элемента g, рассматривать его как перестановку X. если

Полная, взвешенная версия

В более общей и более важной версии теоремы цвета также имеют вес одним или несколькими способами, и цветов может быть бесконечное количество при условии, что набор цветов имеет производящую функцию с конечными коэффициентами. В одномерном случае предположим, что

f(t)=f_{0}+f_{1}t+f_{2}t^{2}+\cdots

является производящей функцией набора цветов, так что существует f _w цветов веса w для каждого целого числа w ≥ 0. В многомерном случае вес каждого цвета представляет собой вектор целых чисел и существует производящая функция f ( t ₁ , t ₂ , ...), который сводит в таблицу количество цветов для каждого заданного вектора весов.

В теореме перечисления используется еще одна многомерная производящая функция, называемая индексом цикла :

Z_{G}(t_{1},t_{2},\ldots ,t_{n})={\frac {1}{|G|}}\sum _{g\in G}t_{1}^{c_{1}(g)}t_{2}^{c_{2}(g)}\cdots t_{n}^{c_{n}(g)}

где n — количество элементов X , а _ck ( g количество k -циклов элемента группы g как перестановки X. ) —

Цветная композиция — это орбита действия группы G на множестве Y ^Х (где Y — набор цветов, а Y ^Х обозначает множество всех функций φ: X → Y ). Вес x такого расположения определяется как сумма весов φ( ) всем x в X. по Теорема утверждает, что производящая функция F количества цветных расположений по весу определяется выражением:

F(t)=Z_{G}(f(t),f(t^{2}),f(t^{3}),\ldots ,f(t^{n}))

или в многомерном случае:

F(t_{1},t_{2},\ldots )=Z_{G}(f(t_{1},t_{2},\ldots ),f(t_{1}^{2},t_{2}^{2},\ldots ),f(t_{1}^{3},t_{2}^{3},\ldots ),\ldots ,f(t_{1}^{n},t_{2}^{n},\ldots )).

Чтобы перейти к упрощенной версии, приведенной ранее, если имеется m цветов и все они имеют вес 0, то f ( t ) = m и

\left|Y^{X}/G\right|=F(0)=Z_{G}(m,m,\ldots ,m)={\frac {1}{|G|}}\sum _{g\in G}m^{c(g)}.

В знаменитом применении подсчета деревьев (см. ниже) и ациклических молекул расположение «цветных бусинок» на самом деле представляет собой расположение расположений, таких как ветви укорененного дерева. Таким образом, производящая функция f для цветов получается из производящей функции F для компоновок, а теорема нумерации Пойа становится рекурсивной формулой.

Примеры

Ожерелья и браслеты

Цветные кубики

Сколькими способами можно раскрасить стороны трехмерного куба в m цветов с точностью до вращения куба? Группа вращения куба C действует на шесть сторон куба, которые эквивалентны бусинкам. Его индекс цикла

Z_{C}(t_{1},t_{2},t_{3},t_{4})={\frac {1}{24}}\left(t_{1}^{6}+6t_{1}^{2}t_{4}+3t_{1}^{2}t_{2}^{2}+8t_{3}^{2}+6t_{2}^{3}\right)

который получается путем анализа действия каждого из 24 элементов C на 6 сторон куба, см. здесь подробности .

Мы принимаем, что все цвета имеют вес 0, и обнаруживаем, что существуют

F(0)=Z_{C}(m,m,m,m)={\frac {1}{24}}\left(m^{6}+3m^{4}+12m^{3}+8m^{2}\right)

разные раскраски.

Графы на трех и четырех вершинах

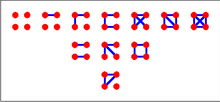
Граф на m вершинах можно интерпретировать как расположение цветных бусин. Множество X «бусинок» — это множество ${\binom {m}{2}}$ возможных ребер, а набор цветов Y = {черный, белый} соответствует ребрам, которые присутствуют (черный) или отсутствуют (белый). Теорему нумерации Пойа можно использовать для вычисления количества графов с точностью до изоморфизма с фиксированным числом вершин или производящей функции этих графов в зависимости от количества ребер, которые они имеют. Для последней цели мы можем сказать, что черное или присутствующее ребро имеет вес 1, а отсутствующее или белое ребро имеет вес 0. Таким образом, $f(t)=1+t$ — производящая функция набора цветов. Соответствующая группа симметрии $G=S_{m},$ симметрическая группа по m буквам. Эта группа действует на множестве X возможных ребер: перестановка φ превращает ребро {a, b} в ребро {φ(a), φ(b)}. С этими определениями класс изоморфизма графов с m вершинами — это то же самое, что орбита действия G на множестве Y ^Х цветных композиций; количество ребер графа равно весу композиции.

Неизоморфные графы на трех вершинах

Восемь графов на трех вершинах (до определения изоморфных графов) показаны справа. Существует четыре класса изоморфизма графов, которые также показаны справа.

Индекс цикла группы S3 _, действующей на множестве трех ребер, равен

Z_{G}(t_{1},t_{2},t_{3})={\frac {1}{6}}\left(t_{1}^{3}+3t_{1}t_{2}+2t_{3}\right)

(получено путем проверки структуры цикла действия элементов группы; см. здесь ). Таким образом, согласно теореме перечисления, производящая функция графов на 3 вершинах с точностью до изоморфизма равна

F(t)=Z_{G}\left(t+1,t^{2}+1,t^{3}+1\right)={\frac {1}{6}}\left((t+1)^{3}+3(t+1)(t^{2}+1)+2(t^{3}+1)\right),

что упрощается до

F(t)=t^{3}+t^{2}+t+1.

Таким образом, существует один граф, каждый из которых имеет от 0 до 3 ребер.

Индекс цикла группы S4 _, действующей на множестве из 6 ребер, равен

Z_{G}(t_{1},t_{2},t_{3},t_{4})={\frac {1}{24}}\left(t_{1}^{6}+9t_{1}^{2}t_{2}^{2}+8t_{3}^{2}+6t_{2}t_{4}\right)

(см. здесь .) Следовательно

F(t)=Z_{G}\left(t+1,t^{2}+1,t^{3}+1,t^{4}+1\right)={\frac {(t+1)^{6}+9(t+1)^{2}(t^{2}+1)^{2}+8(t^{3}+1)^{2}+6(t^{2}+1)(t^{4}+1)}{24}}

что упрощается до

F(t)=t^{6}+t^{5}+2t^{4}+3t^{3}+2t^{2}+t+1.

Эти графики показаны справа.

Тройные деревья с укоренением

Множество T ₃ корневых троичных деревьев состоит из корневых деревьев, у которых каждый узел (или нелистовая вершина) имеет ровно три потомка (листья или поддеревья). Небольшие тройные деревья показаны справа. Обратите внимание, что корневые троичные деревья с n узлами эквивалентны корневым деревьям с n вершинами степени не выше 3 (без учета листьев). В общем, два корневых дерева изоморфны, если одно можно получить из другого путем перестановки дочерних элементов его узлов. Другими словами, группа, действующая на детей узла, является симметричной S3 _. группой Мы определяем вес такого троичного дерева как количество узлов (или нелистовых вершин).

Тернарные деревья с корнем на 0, 1, 2, 3 и 4 узлах (= нелистовые вершины). Корень показан синим цветом, листья не показаны. Каждый узел имеет столько листьев, чтобы число его потомков было равно 3.

Можно рассматривать корневое троичное дерево как рекурсивный объект, который представляет собой либо лист, либо узел с тремя дочерними элементами, которые сами являются корневыми троичными деревьями. Эти дети эквивалентны четкам; симметрической группы S3 _равен индекс цикла действующей на них

Z_{S_{3}}(t_{1},t_{2},t_{3})={\frac {t_{1}^{3}+3t_{1}t_{2}+2t_{3}}{6}}.

Теорема перечисления Пойа переводит рекурсивную структуру корневых троичных деревьев в функциональное уравнение для производящей функции F(t) корневых троичных деревьев по числу узлов. Это достигается путем «раскрашивания» трех дочерних элементов корневыми троичными деревьями, взвешенными по номеру узла, так что функция генерации цвета определяется выражением $f(t)=F(t)$ что по теореме перечисления дает

{\frac {F(t)^{3}+3F(t)F(t^{2})+2F(t^{3})}{6}}

как производящая функция для корневых троичных деревьев, взвешенных на единицу меньше номера узла (поскольку сумма весов дочерних элементов не учитывает корень), так что

F(t)=1+t\cdot {\frac {F(t)^{3}+3F(t)F(t^{2})+2F(t^{3})}{6}}.

Это эквивалентно следующей рекуррентной формуле для числа t _n корневых троичных деревьев с n узлами:

{\begin{aligned}t_{0}&=1\\t_{n+1}&={\frac {1}{6}}\left(\sum _{a+b+c=n}t_{a}t_{b}t_{c}+3\sum _{a+2b=n}t_{a}t_{b}+2\sum _{3a=n}t_{a}\right)\end{aligned}}

где a , b и c — целые неотрицательные числа.

Первые несколько значений $t_{n}$ являются

1, 1, 1, 2, 4, 8, 17, 39, 89, 211, 507, 1238, 3057, 7639, 19241 (последовательность A000598 в OEIS ).

Доказательство теоремы

Упрощенная форма теоремы перечисления Пойа следует из леммы Бернсайда , которая гласит, что число орбит раскрасок есть среднее число элементов $Y^{X}$ фиксируется перестановкой g группы G по всем перестановкам g . Взвешенная версия теоремы имеет по существу то же доказательство, но с уточненной формой леммы Бернсайда для взвешенного перечисления. Это эквивалентно применению леммы Бернсайда отдельно к орбитам разного веса.

Для более понятных обозначений пусть $x_{1},x_{2},\ldots$ — переменные производящей функции f функции $Y$ . Учитывая вектор весов $\omega$ , позволять $x^{\omega }$ обозначим соответствующий мономиальный член функции f . Применение леммы Бернсайда к весовым орбитам $\omega$ , число орбит этого веса равно

{\frac {1}{|G|}}\sum _{g\in G}\left|(Y^{X})_{\omega ,g}\right|

где $(Y^{X})_{\omega ,g}$ – набор раскрасок веса $\omega$ которые также фиксируются g . Если затем суммировать по всем возможным весам, мы получим

F(x_{1},x_{2},\ldots )={\frac {1}{|G|}}\sum _{g\in G,\omega }x^{\omega }\left|(Y^{X})_{\omega ,g}\right|.

При этом элемент группы g с циклической структурой $j_{1}(g),j_{2}(g),\ldots ,j_{n}(g)$ будет способствовать сроку

t_{1}^{j_{1}(g)}t_{2}^{j_{2}(g)}\cdots t_{n}^{j_{n}(g)}

к индексу цикла G . Элемент g фиксирует элемент $\phi \in Y^{X}$ тогда и только тогда, когда функция φ постоянна на каждом цикле q функции g . Для каждого такого цикла q производящая функция по весу | д | одинаковые цвета из множества, пронумерованного f, — это