R-четность

R-четность — это концепция в физике элементарных частиц . В минимальной суперсимметричной стандартной модели барионное и лептонное число больше не сохраняются всеми перенормируемыми связями в теории. Поскольку сохранение барионного и лептонного числа было проверено очень точно, эти связи должны быть очень малыми, чтобы не противоречить экспериментальным данным. R-четность – это $\mathbb {Z} _{2}$ симметрия, действующая на поля минимальной суперсимметричной стандартной модели (MSSM), которая запрещает эти связи и может быть определена как ^[1]

P_{\mathrm {R} }=(-1)^{3B+L+2s},

или, что то же самое, как

P_{\mathrm {R} }=(-1)^{3(B-L)+2s},

где $s$ — спин , $B$ — барионное число, а $L$ — лептонное число. Все частицы Стандартной модели имеют R-четность +1, а суперсимметричные частицы имеют R-четность -1.

Обратите внимание, что существуют разные формы паритета с разными эффектами и принципами, не следует путать этот паритет ни с каким другим паритетом .

Кандидат на темную материю

При сохранении R-четности легчайшая суперсимметричная частица ( LSP ) не может распасться. Таким образом, эта легчайшая частица (если она существует) может объяснить наблюдаемую недостающую массу Вселенной, которую обычно называют темной материей . ^[2] Чтобы соответствовать наблюдениям, предполагается, что эта частица имеет массу 100 ГэВ/ с. ² это 1 ТэВ/ c ², нейтрален и взаимодействует только посредством слабых взаимодействий и гравитационных взаимодействий . Ее часто называют слабо взаимодействующей массивной частицей или вимпом.

Обычно кандидат темной материи MSSM представляет собой смесь электрослабых гаугино и хиггсино и называется нейтралино . В расширениях MSSM возможно, что нейтрино станет кандидатом на роль темной материи. Другой возможностью является гравитино , которое взаимодействует только посредством гравитационных взаимодействий и не требует строгой R-четности.

Связи MSSM, нарушающие R-четность

Перенормируемые связи MSSM, нарушающие R-четность:

$\int d^{2}\theta \;\lambda _{1}\;U^{c}D^{c}D^{c}$ нарушает $B$ на 1 единицу

Самое сильное ограничение, связанное только с этой связью, связано с ненаблюдением нейтрон-антинейтронных колебаний.

$\int d^{2}\theta \;\lambda _{2}\;QD^{c}L$ нарушает $L$ на 1 единицу

Самым сильным ограничением, связанным только с этой связью, является нарушение универсальности константы Ферми. $G_{F}$ при распаде кваркового и лептонного заряженного тока.

$\int d^{2}\theta \;\lambda _{3}\;LE^{c}L$ нарушает $L$ на 1 единицу

Самым сильным ограничением, связанным только с этой связью, является нарушение универсальности константы Ферми при распаде лептонного заряженного тока.

$\int d^{2}\theta \;\kappa \;LH_{u}$ нарушает $L$ на 1 единицу

Самым сильным ограничением, связанным только с этой связью, является то, что она приводит к большой массе нейтрино.

Хотя ограничения на одиночные связи достаточно сильны, если несколько связей объединяются вместе, они приводят к распаду протона . Таким образом, существуют дополнительные максимальные границы значений связей из максимальных границ скорости распада протона.

Распад протона

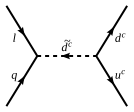
Без сохранения и принятия барионного и лептонного числа ${\mathcal {O}}(1)$ Для связей, нарушающих R-четность, протон может распасться примерно за 10 ⁻² секунд или, если минимальное нарушение вкуса предполагается , время жизни протона может быть увеличено до 1 года. Поскольку наблюдается время жизни протона больше 10 ³³ до 10 ³⁴ лет (в зависимости от точного канала распада), это крайне невыгодно для модели. R-четность обнуляет все перенормируемые барионные и лептонные связи, нарушающие числа, а протон стабилен на перенормируемом уровне, а время жизни протона увеличивается до 10 ³² лет и практически соответствует современным данным наблюдений.

Поскольку распад протона включает одновременное нарушение как лептонного, так и барионного числа, ни одна перенормируемая связь, нарушающая R-четность, не приводит к распаду протона. Это побудило к изучению нарушения R-четности, когда только один набор связей, нарушающих R-четность, не равен нулю, что иногда называют гипотезой доминирования одиночной связи.

Возможное происхождение R-четности

Очень привлекательный способ мотивировать R-четность — это $непрерывная калибровочная симметрия B — L$ , которая спонтанно нарушается в масштабе, недоступном для текущих экспериментов. Непрерывный $U(1)_{B-L}$ нарушающие $B$ и $L.$ запрещает перенормируемые члены , ^[3]^[4]^[5]^[6] Если $U(1)_{B-L}$ нарушается только скалярными вакуумными средними значениями (или другими параметрами порядка), которые несут четные целые значения 3( $B - L$ ) , то существует точно сохраняющаяся дискретная остаточная подгруппа, которая имеет желаемые свойства. ^[7]^[8]^[9]^[10]^[11] Ключевой вопрос состоит в том, чтобы определить, развивает ли снейтрино (суперсимметричный партнер нейтрино), которое является нечетным при R-четности, вакуумное математическое ожидание. На феноменологических основаниях можно показать, что этого не может произойти ни в одной теории, где $U(1)_{B-L}$ нарушается на масштабе, значительно превышающем электрослабой . Это верно для любой теории, основанной на крупномасштабном качающемся механизме . ^[12] Как следствие, в таких теориях R-четность остается точной при всех энергиях.

Это явление может возникнуть как автоматическая симметрия в SO(10) теориях Великого объединения . Это естественное появление R-четности возможно, потому что в SO (10) фермионы Стандартной модели возникают из 16-мерного спинорного представления , а Хиггс возникает из 10-мерного векторного представления. Чтобы реализовать инвариантную связь SO(10), необходимо иметь четное число спинорных полей (т.е. иметь спинорную четность). После нарушения симметрии GUT эта спинорная четность переходит в R-четность до тех пор, пока для нарушения симметрии GUT не использовались спинорные поля. Построены явные примеры таких теорий SO(10). ^[13]^[14]

См. также

R-симметрия

Ссылки

^ Мартин, СП (6 сентября 2011 г.). «Букварь суперсимметрии». Расширенная серия по направлениям физики высоких энергий . 18 :1–98. arXiv : hep-ph/9709356 . дои : 10.1142/9789812839657_0001 . ISBN 978-981-02-3553-6 . S2CID 118973381 .
^ Юнгман, Г.; Камионковски, М.; Грист, К. (1996). «Суперсимметричная темная материя». Отчеты по физике . 267 (5–6): 195–373. arXiv : hep-ph/9506380 . Бибкод : 1996PhR...267..195J . дои : 10.1016/0370-1573(95)00058-5 . S2CID 119067698 .
^ Мохапатра, Р.Н. (1986). «Новый вклад в безнейтринный двойной бета-распад в суперсимметричных теориях». Физический обзор D . 34 (11): 3457–3461. Бибкод : 1986PhRvD..34.3457M . дои : 10.1103/PhysRevD.34.3457 . ПМИД 9957083 .
^ Фонт, А.; Ибаньес, Ле; Кеведо, Ф. (1989). «Означает ли стабильность протона существование дополнительного Z ⁰?» (PDF) . Physics Letters B. 228 ( 1): 79–88. Бибкод : 1989PhLB..228...79F . doi : 10.1016/0370-2693(89)90529-7 .
^ Мартин, СП (1992). «Некоторые простые критерии калиброванной R-паритета». Физический обзор D . 46 (7): R2769–R2772. arXiv : hep-ph/9207218 . Бибкод : 1992PhRvD..46.2769M . дои : 10.1103/PhysRevD.46.R2769 . ПМИД 10015267 . S2CID 14821065 .
^ Мартин, СП (1996). «Следствия суперсимметричных моделей с естественным сохранением R-четности». Физический обзор D . 54 (3): 2340–2348. arXiv : hep-ph/9602349 . Бибкод : 1996PhRvD..54.2340M . дои : 10.1103/PhysRevD.54.2340 . ПМИД 10020912 . S2CID 5751474 .
^ Файе, П. (1975). «Суперкалибровочное инвариантное расширение механизма Хиггса и модель электрона и его нейтрино». Ядерная физика Б . 90 : 104–124. Бибкод : 1975NuPhB..90..104F . дои : 10.1016/0550-3213(75)90636-7 .
^ Салам, А.; Стратди, Дж. (1975). «Суперсимметрия и сохранение фермионного числа». Ядерная физика Б . 87 (1): 85–92. Бибкод : 1975НуФБ..87...85С . дои : 10.1016/0550-3213(75)90253-9 .
^ Фаррар, Греция; Вайнберг, С. (1983). «Суперсимметрия при обычных энергиях. II. R-инвариантность, бозоны Голдстоуна и массы калибровочных фермионов». Физический обзор D . 27 (11): 2732. Бибкод : 1983PhRvD..27.2732F . дои : 10.1103/PhysRevD.27.2732 .
^ Файе, П. (1977). «Спонтанно нарушенные суперсимметричные теории слабого, электромагнитного и сильного взаимодействий». Буквы по физике Б. 69 (4): 489–494. Бибкод : 1977PhLB...69..489F . дои : 10.1016/0370-2693(77)90852-8 .
^ Фаррар, Греция; Файе, П. (1978). «Феноменология рождения, распада и обнаружения новых адронных состояний, связанных с суперсимметрией». Буквы по физике Б. 76 (5): 575. Бибкод : 1978PhLB...76..575F . дои : 10.1016/0370-2693(78)90858-4 .
^ Аулах, CS; Мелфо, А.; Рашин А.; Сеньянович, Г. (1998). «Суперсимметрия и крупномасштабная симметрия слева и справа». Физический обзор D . 58 (11): 115007. arXiv : hep-ph/9712551 . Бибкод : 1998PhRvD..58k5007A . doi : 10.1103/PhysRevD.58.115007 . S2CID 43296921 .
^ Аулах, CS; Байц, Б.; Мелфо, А.; Рашин А.; Сеньянович, Г. (2001). «Теория SO (10) R-четности и массы нейтрино». Ядерная физика Б . 597 (1–3): 89–109. arXiv : hep-ph/0004031 . Бибкод : 2001НуФБ.597...89А . дои : 10.1016/S0550-3213(00)00721-5 . S2CID 119100803 .
^ Аулах, CS; Байц, Б.; Мелфо, А.; Сеньянович, Г.; Виссани, Ф. (2004). «Минимальная суперсимметричная теория великого объединения». Буквы по физике Б. 588 (3–4): 196–202. arXiv : hep-ph/0306242 . Бибкод : 2004PhLB..588..196A . дои : 10.1016/j.physletb.2004.03.031 . S2CID 119401374 .

Внешние ссылки

Барбье, Р.; и др. (2005). «Суперсимметрия, нарушающая R-четность». Отчеты по физике . 420 (1–6): 1–195. arXiv : hep-ph/0406039 . Бибкод : 2005ФР...420....1Б . doi : 10.1016/j.physrep.2005.08.006 .
«Нарушение R-четности…» xstructure.inr.ac.ru .
«Нарушение R-четности…» ФНАЛ . Архивировано из оригинала 28 мая 2010 г.

[1] Мартин, СП (6 сентября 2011 г.). «Букварь суперсимметрии». Расширенная серия по направлениям физики высоких энергий . 18 :1–98. arXiv : hep-ph/9709356 . дои : 10.1142/9789812839657_0001 . ISBN 978-981-02-3553-6 . S2CID 118973381 .

[2] Юнгман, Г.; Камионковски, М.; Грист, К. (1996). «Суперсимметричная темная материя». Отчеты по физике . 267 (5–6): 195–373. arXiv : hep-ph/9506380 . Бибкод : 1996PhR...267..195J . дои : 10.1016/0370-1573(95)00058-5 . S2CID 119067698 .

[3] Мохапатра, Р.Н. (1986). «Новый вклад в безнейтринный двойной бета-распад в суперсимметричных теориях». Физический обзор D . 34 (11): 3457–3461. Бибкод : 1986PhRvD..34.3457M . дои : 10.1103/PhysRevD.34.3457 . ПМИД 9957083 .

[4] Фонт, А.; Ибаньес, Ле; Кеведо, Ф. (1989). «Означает ли стабильность протона существование дополнительного Z ⁰?» (PDF) . Physics Letters B. 228 ( 1): 79–88. Бибкод : 1989PhLB..228...79F . doi : 10.1016/0370-2693(89)90529-7 .

[5] Мартин, СП (1992). «Некоторые простые критерии калиброванной R-паритета». Физический обзор D . 46 (7): R2769–R2772. arXiv : hep-ph/9207218 . Бибкод : 1992PhRvD..46.2769M . дои : 10.1103/PhysRevD.46.R2769 . ПМИД 10015267 . S2CID 14821065 .

[6] Мартин, СП (1996). «Следствия суперсимметричных моделей с естественным сохранением R-четности». Физический обзор D . 54 (3): 2340–2348. arXiv : hep-ph/9602349 . Бибкод : 1996PhRvD..54.2340M . дои : 10.1103/PhysRevD.54.2340 . ПМИД 10020912 . S2CID 5751474 .

[7] Файе, П. (1975). «Суперкалибровочное инвариантное расширение механизма Хиггса и модель электрона и его нейтрино». Ядерная физика Б . 90 : 104–124. Бибкод : 1975NuPhB..90..104F . дои : 10.1016/0550-3213(75)90636-7 .

[8] Салам, А.; Стратди, Дж. (1975). «Суперсимметрия и сохранение фермионного числа». Ядерная физика Б . 87 (1): 85–92. Бибкод : 1975НуФБ..87...85С . дои : 10.1016/0550-3213(75)90253-9 .

[9] Фаррар, Греция; Вайнберг, С. (1983). «Суперсимметрия при обычных энергиях. II. R-инвариантность, бозоны Голдстоуна и массы калибровочных фермионов». Физический обзор D . 27 (11): 2732. Бибкод : 1983PhRvD..27.2732F . дои : 10.1103/PhysRevD.27.2732 .

[10] Файе, П. (1977). «Спонтанно нарушенные суперсимметричные теории слабого, электромагнитного и сильного взаимодействий». Буквы по физике Б. 69 (4): 489–494. Бибкод : 1977PhLB...69..489F . дои : 10.1016/0370-2693(77)90852-8 .

[11] Фаррар, Греция; Файе, П. (1978). «Феноменология рождения, распада и обнаружения новых адронных состояний, связанных с суперсимметрией». Буквы по физике Б. 76 (5): 575. Бибкод : 1978PhLB...76..575F . дои : 10.1016/0370-2693(78)90858-4 .

[12] Аулах, CS; Мелфо, А.; Рашин А.; Сеньянович, Г. (1998). «Суперсимметрия и крупномасштабная симметрия слева и справа». Физический обзор D . 58 (11): 115007. arXiv : hep-ph/9712551 . Бибкод : 1998PhRvD..58k5007A . doi : 10.1103/PhysRevD.58.115007 . S2CID 43296921 .

[13] Аулах, CS; Байц, Б.; Мелфо, А.; Рашин А.; Сеньянович, Г. (2001). «Теория SO (10) R-четности и массы нейтрино». Ядерная физика Б . 597 (1–3): 89–109. arXiv : hep-ph/0004031 . Бибкод : 2001НуФБ.597...89А . дои : 10.1016/S0550-3213(00)00721-5 . S2CID 119100803 .

[14] Аулах, CS; Байц, Б.; Мелфо, А.; Сеньянович, Г.; Виссани, Ф. (2004). «Минимальная суперсимметричная теория великого объединения». Буквы по физике Б. 588 (3–4): 196–202. arXiv : hep-ph/0306242 . Бибкод : 2004PhLB..588..196A . дои : 10.1016/j.physletb.2004.03.031 . S2CID 119401374 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]