Гауссов логарифм

В математике логарифмы сложения и вычитания или гауссовы логарифмы могут использоваться для нахождения логарифмов суммы . и разности пары значений, логарифмы которых известны, не зная самих значений ^[1]

Их математические основы восходят к Зеккини Леонелли. ^[2]^[3] и Карл Фридрих Гаусс ^[4]^[1]^[5] в начале 1800-х годов. ^[2]^[3]^[4]^[1]^[5]

Операции сложения и вычитания можно рассчитать по формуле:

\log _{b}{\big (}|X|+|Y|{\big )}=x+s_{b}(y-x),

\log _{b}{\big (}{\big |}|X|-|Y|{\big |}{\big )}=x+d_{b}(y-x),

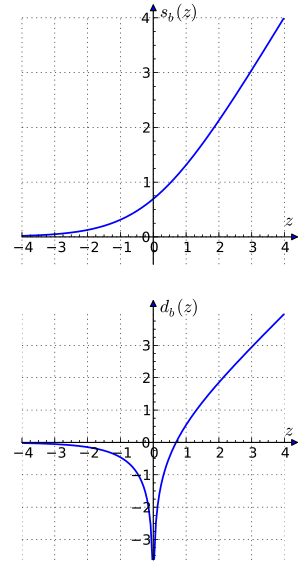
где $x=\log _{b}\!|X|$ , $y=\log _{b}\!|Y|$ , функция «сумма» определяется формулой $s_{b}(z)=\log _{b}(1+b^{z})$ и функция «разности» по $d_{b}(z)=\log _{b}\!|1-b^{z}|$ . Функции $s_{b}(z)$ и $d_{b}(z)$ также известны как гауссовы логарифмы .

Для натуральных логарифмов с $b=e$ существуют следующие тождества с гиперболическими функциями :

s_{e}(z)=\ln 2+{\frac {z}{2}}+\ln \left(\cosh {\frac {z}{2}}\right)

d_{e}(z)=\ln 2+{\frac {z}{2}}+\ln \left|\,\sinh {\frac {z}{2}}\right|

Это показывает, что $s_{e}$ имеет разложение Тейлора , в котором все члены, кроме первого, рациональны , а все нечетные члены, кроме линейного, равны нулю.

Упрощение умножения, деления, получения корней и степеней уравновешивается стоимостью оценки этих функций для сложения и вычитания.

См. также

Ссылки

^ Jump up to: ^а ^б ^с «Логарифм: сложение и вычитание, или Гауссовы логарифмы» . Британская энциклопедия, одиннадцатое издание .
^ Jump up to: ^а ^б Леонелли, Зеккини (1803) [1802]. Логарифмическое дополнение. Теория дополнительных и дидуктивных логарифмов (на французском языке). Бордо: Броссье. (Примечание: 1802/1803 — это XI год по французскому республиканскому календарю .)
^ Jump up to: ^а ^б Леонарди, Готфрид Вильгельм (1806). Логарифмические дополнения ЛЕОНЕЛЛИ как вклад в восполнение недостатков обычных логарифмических таблиц. Перевод с французского с некоторыми дополнениями ГОТФРИДА ВИЛЬГЕЛЬМА ЛЕОНХАРДИ, младшего лейтенанта избирательного саксонского корпуса полевой артиллерии (на немецком языке). Дрезден: Walther'sche Hofbuchhandlung. Зеккини Леонелли (Примечание. Расширенный перевод « Supplement logarithmique. Théorie des logarithmes addels et diductifs» .)
^ Jump up to: ^а ^б Гаусс, Иоганн Карл Фридрих (12 февраля 1808 г.). «ЛЕОНЕЛЛИ, Логарифмические добавки». Общая литературная газета (на немецком языке) (45). Галле-Лейпциг: 353–356.
^ Jump up to: ^а ^б Даннингтон, Гай Уолдо (2004) [1955]. Грей, Джереми; Дозе, Фриц-Эгберт (ред.). Карл Фридрих Гаусс – титан науки . Серия «Спектр» (переработанная ред.). Математическая ассоциация Америки (МАА). ISBN 978-0-88385-547-8 . ISBN 0-88385-547-X .

Дальнейшее чтение

Старк, Брюс Д. (1997) [1995]. Таблицы Старка для определения лунного расстояния и определения всемирного времени с помощью секстантных наблюдений, включая удобный способ отточить навыки небесной навигации на суше (2-е изд.). Публикации Звездного пути. ISBN 978-0914025214 . 091402521X . Проверено 2 декабря 2015 г. (Примечание. Содержит таблицу гауссовских логарифмов lg (1+10 ^-х).)
Каливода, Ян (30 июля 2003 г.). «Брюс Старк - Таблицы для определения лунного расстояния и определения времени по Гринвичу с помощью секстантных наблюдений (1995, 1997)» (обзор). Прага, Чехия. Архивировано из оригинала 12 января 2004 г. Проверено 2 декабря 2015 г. …] Брюс Старк […] использует гауссовы логарифмы, которые позволяют оставаться в мире логарифмов все время вычислений и превращать сложение натуральных чисел в сложение и вычитание их обычных и специальных логарифмических значений с помощью специальной таблицы. . Это гораздо проще, чем приводить бревна к их естественным значениям, складывать их и снова конвертировать в бревна. Более того, гауссовские журналы дают большую точность результатов, чем традиционный метод вычислений, и помогают 5-значным значениям журнала быть достаточно точными для этого метода. […] Использование Брюсом «гауссианов» является оригинальным в области навигации. Я не знаю другого примера их использования моряками или авиаторами - за исключением советских штурманов, у которых в стандартной таблице были установлены гауссианы до ок. 1960. […] хаверсина , что не допускалось в советскую навигационную практику. […] Гауссианцы мирно сотрудничают с хаверсинусами в рационализации процедуры LD […] [1] [2]
Кремер, Герман (29 августа 2002 г.). «Логарифам гауссовского сложения исполняется 200 лет» . de.sci.mathematik (на немецком языке). Архивировано из оригинала 7 июля 2018 г. Проверено 7 июля 2018 г.
Кюн, Клаус (2008). «CF Гаусс и логарифмы» (PDF) (на немецком языке). Аллинг-Бибург, Германия. Архивировано (PDF) из оригинала 14 июля 2018 г. Проверено 14 июля 2018 г.

[Theodora-1] Jump up to: ^а ^б ^с «Логарифм: сложение и вычитание, или Гауссовы логарифмы» . Британская энциклопедия, одиннадцатое издание .

[Leonelli_1802-2] Jump up to: ^а ^б Леонелли, Зеккини (1803) [1802]. Логарифмическое дополнение. Теория дополнительных и дидуктивных логарифмов (на французском языке). Бордо: Броссье. (Примечание: 1802/1803 — это XI год по французскому республиканскому календарю .)

[Leonhardi_1806-3] Jump up to: ^а ^б Леонарди, Готфрид Вильгельм (1806). Логарифмические дополнения ЛЕОНЕЛЛИ как вклад в восполнение недостатков обычных логарифмических таблиц. Перевод с французского с некоторыми дополнениями ГОТФРИДА ВИЛЬГЕЛЬМА ЛЕОНХАРДИ, младшего лейтенанта избирательного саксонского корпуса полевой артиллерии (на немецком языке). Дрезден: Walther'sche Hofbuchhandlung. Зеккини Леонелли (Примечание. Расширенный перевод « Supplement logarithmique. Théorie des logarithmes addels et diductifs» .)

[Gauss_1808-4] Jump up to: ^а ^б Гаусс, Иоганн Карл Фридрих (12 февраля 1808 г.). «ЛЕОНЕЛЛИ, Логарифмические добавки». Общая литературная газета (на немецком языке) (45). Галле-Лейпциг: 353–356.

[Dunnington_2004-5] Jump up to: ^а ^б Даннингтон, Гай Уолдо (2004) [1955]. Грей, Джереми; Дозе, Фриц-Эгберт (ред.). Карл Фридрих Гаусс – титан науки . Серия «Спектр» (переработанная ред.). Математическая ассоциация Америки (МАА). ISBN 978-0-88385-547-8 . ISBN 0-88385-547-X .

[1]

[2]

[3]

[4]

[5]