Цепь Маркова с дискретным временем

В теории вероятности цепь Маркова с дискретным временем ( DTMC ) представляет собой последовательность случайных величин, известную как случайный процесс , в котором значение следующей переменной зависит только от значения текущей переменной, а не от каких-либо переменных в прошлом. . Например, машина может иметь два состояния A и E. : Когда он находится в состоянии A , существует 40% вероятность его перехода в состояние E и 60% вероятность того, что он останется в A. состоянии Когда он находится в состоянии E , существует 70% вероятность его перехода в A и 30% вероятность того, что он останется E. в Последовательность состояний машины представляет собой цепь Маркова. Если обозначить цепочку через $X_{0},X_{1},X_{2},...$ затем $X_{0}$ это состояние, в котором машина запускается и $X_{10}$ – случайная величина, описывающая его состояние после 10 переходов. Процесс продолжается вечно, индексируясь натуральными числами .

Примером случайного процесса, не являющегося цепью Маркова, является модель машины, которая имеет состояния A и E и переходит в A из любого состояния с вероятностью 50 %, если она когда-либо посещала A раньше, и вероятностью 20 %, если она уже посещала A. никогда раньше не посещал A (оставляя вероятность 50% или 80%, что машина переместится в E ). Это связано с тем, что поведение машины зависит от всей истории: если машина находится в E , у нее может быть 50% или 20% шанс перейти в A , в зависимости от ее прошлых значений. Следовательно, оно не обладает марковским свойством .

Цепь Маркова можно описать стохастической матрицей , в которой перечислены вероятности перехода в каждое состояние из любого отдельного состояния. Из этой матрицы можно вычислить вероятность пребывания в определенном состоянии на n шагах в будущем. Пространство состояний цепи Маркова можно разделить на взаимодействующие классы, которые описывают, какие состояния достижимы друг из друга (за один переход или за несколько). Каждое состояние можно описать как переходное или повторяющееся, в зависимости от вероятности того, что цепочка когда-либо вернется в это состояние. Цепи Маркова могут обладать такими свойствами, как периодичность, обратимость и стационарность. Цепь Маркова с непрерывным временем похожа на цепь Маркова с дискретным временем, но она перемещает состояния непрерывно во времени, а не дискретными шагами по времени. Другие случайные процессы могут удовлетворять свойству Маркова — свойству, согласно которому прошлое поведение не влияет на процесс, а влияет только на настоящее состояние.

Определение

Цепь Маркова с дискретным временем представляет собой последовательность случайных величин. $X_{0},X_{1},X_{2},...$ со свойством Маркова , а именно, что вероятность перехода в следующее состояние зависит только от текущего состояния, а не от предыдущих состояний:

\Pr(X_{n+1}=x\mid X_{1}=x_{1},X_{2}=x_{2},\ldots ,X_{n}=x_{n})=\Pr(X_{n+1}=x\mid X_{n}=x_{n}),

если обе условные вероятности корректно определены, т. е. если

\Pr(X_{1}=x_{1},\ldots ,X_{n}=x_{n})>0.

Возможные значения X _i образуют счетное множество S, называемое пространством состояний цепи. ^[1]

Цепи Маркова часто описываются последовательностью ориентированных графов , где ребра графа n помечены вероятностями перехода из одного состояния в момент времени n в другие состояния в момент времени n + 1, $\Pr(X_{n+1}=x\mid X_{n}=x_{n}).$ Та же информация представлена матрицей перехода от времени n ко времени n + 1. Однако часто предполагается, что цепи Маркова однородны во времени (см. варианты ниже), и в этом случае график и матрица независимы от n и, таким образом, не представлены в виде последовательностей.

Эти описания подчеркивают структуру цепи Маркова, которая не зависит от начального распределения. $\Pr(X_{1}=x_{1}).$ Когда цепь однородна во времени, ее можно интерпретировать как конечный автомат, присваивающий вероятность перехода из каждой вершины или состояния в соседнюю. Вероятность $\Pr(X_{n}=x\mid X_{1}=x_{1})$ состояния машины можно анализировать как статистическое поведение машины с элементом $x_{1}$ пространства состояний в качестве входных данных или как поведение машины с начальным распределением $\Pr(X_{1}=y)=[x_{1}=y]$ состояний в качестве входных данных, где $[P]$ это скобка Айверсона . ^{[ нужна ссылка ]}

Вариации

Однородные во времени цепи Маркова (или стационарные цепи Маркова) — это процессы, в которых

\Pr(X_{n+1}=x\mid X_{n}=y)=\Pr(X_{n}=x\mid X_{n-1}=y)

для всех н . Вероятность перехода не зависит от n . ^[1]

Цепь Маркова с памятью (или цепь Маркова порядка m )

где m конечно, является процессом, удовлетворяющим

{\begin{aligned}&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{1}=x_{1})\\={}&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{n-m}=x_{n-m}){\text{ for }}n>m\end{aligned}}

Другими словами, будущее состояние зависит от прошлых m состояний. Можно построить цепочку

(Y_{n})

от

(X_{n})

который обладает «классическим» марковским свойством, принимая в качестве пространства состояний упорядоченные m -кортежи значений X , т.е.

Y_{n}=\left(X_{n},X_{n-1},\ldots ,X_{n-m+1}\right)

. ^{[ нужна ссылка ]}

n- шаговые переходы

Вероятность перехода из состояния i в состояние j за n шагов по времени равна

p_{ij}^{(n)}=\Pr(X_{n}=j\mid X_{0}=i)

и одношаговый переход

p_{ij}=\Pr(X_{1}=j\mid X_{0}=i).

Для однородной по времени цепи Маркова:

p_{ij}^{(n)}=\Pr(X_{k+n}=j\mid X_{k}=i)

и

p_{ij}=\Pr(X_{k+1}=j\mid X_{k}=i).

Вероятности n -шагового перехода удовлетворяют уравнению Чепмена–Колмогорова , согласно которому для любого k такого, что 0 < k < n ,

p_{ij}^{(n)}=\sum _{r\in S}p_{ir}^{(k)}p_{rj}^{(n-k)}

где S — пространство состояний цепи Маркова. ^[1]

Маргинальное распределение Pr( X _n = x ) — это распределение по состояниям в момент времени n . Начальное распределение Pr( X ₀ = x ). Эволюция процесса за один временной шаг описывается формулой

\Pr(X_{n}=j)=\sum _{r\in S}p_{rj}\Pr(X_{n-1}=r)=\sum _{r\in S}p_{rj}^{(n)}\Pr(X_{0}=r).

(Верхний индекс ( n ) является индексом , а не показателем степени ).

Общение классов и свойств

Состояние j называется доступным из состояния i (записывается i → j ), если система, запущенная в состоянии i, имеет ненулевую вероятность перехода в состояние j в какой-то момент. Формально состояние j доступно из состояния i , если существует целое число n _ij ≥ 0 такое, что

\Pr(X_{n_{ij}}=j\mid X_{0}=i)=p_{ij}^{(n_{ij})}>0.

состояние i Говорят, что взаимодействует с состоянием j (записывается i ↔ j ), если и i → j, и j → i . Коммуникационный класс — это максимальный набор состояний C, такой, что каждая пара состояний в C взаимодействует друг с другом. Коммуникация — это отношение эквивалентности , а взаимодействующие классы — это классы эквивалентности этого отношения. ^[1]

Коммуникирующий класс является закрытым, если вероятность выхода из класса равна нулю, а именно, если i находится в C , а j нет, то j недоступен из i . ^[1] Набор взаимодействующих классов образует ориентированный ациклический граф, наследуя стрелки из исходного пространства состояний. Коммуникационный класс является закрытым тогда и только тогда, когда в этом графе у него нет исходящих стрелок.

Состояние i называется существенным или окончательным, если для всех j таких, что i → j, также верно, что j → i . Состояние i несущественно, если оно не существенно. ^[2] Состояние является окончательным тогда и только тогда, когда его взаимодействующий класс закрыт.

Цепь Маркова называется неприводимой, если ее пространство состояний представляет собой единый взаимодействующий класс; другими словами, если из любого состояния можно попасть в любое состояние. ^[1]^[3]^: 20

Периодичность

Государство $i$ имеет период $k$ если таковые имеются, возвращение в состояние $i$ должно встречаться кратно $k$ временные шаги. Формально период государственного $i$ определяется как

k=\gcd\{n>0:\Pr(X_{n}=i\mid X_{0}=i)>0\}

(где $\gcd$ — наибольший общий делитель ) при условии, что это множество не пусто. В противном случае период не определен. ^[1] Обратите внимание, что хотя состояние имеет период $k$ , возможно, не удастся достичь состояния в $k$ шаги. Например, предположим, что можно вернуться в состояние в $\{6,~8,~10,~12,\dots \}$ временные шаги; $k$ было бы $2$ , Несмотря на то $2$ не отображается в этом списке.

Если $k=1$ , то состояние называется апериодическим. В противном случае ( $k>1$ ), состояние называется периодическим с периодом $k$ . Периодичность — это свойство класса, то есть, если состояние имеет период $k$ тогда каждое состояние в своем взаимодействующем классе имеет период $k$ . ^[1]

Кратковременность и повторение

Состояние i называется переходным, если, учитывая, что мы начинаем в состоянии i , существует ненулевая вероятность того, что мы никогда не вернемся в i . Формально, пусть случайная величина T _i будет первым временем возврата в состояние i («время попадания»):

T_{i}=\inf\{n\geq 1:X_{n}=i\}.

Число

f_{ii}^{(n)}=\Pr(T_{i}=n\mid X_{0}=i)

— вероятность того, что мы вернемся в состояние i впервые после n шагов.Следовательно, состояние i является переходным, если

\Pr(T_{i}<\infty \mid X_{0}=i)=\sum _{n=1}^{\infty }f_{ii}^{(n)}<1.

Состояние i является повторяющимся (или постоянным), если оно не является временным. Повторяемость и кратковременность являются свойствами класса, то есть они либо справедливы, либо не справедливы в равной степени для всех членов взаимодействующего класса. ^[1]

Состояние i является повторяющимся тогда и только тогда, когда ожидаемое количество посещений i бесконечно: ^[1]

\sum _{n=0}^{\infty }p_{ii}^{(n)}=\infty .

Положительный рецидив

Даже если время попадания конечно с вероятностью 1, оно не обязательно должно иметь конечное математическое ожидание . Среднее время повторения в состоянии i — это ожидаемое время возврата M _i :

M_{i}=E[T_{i}]=\sum _{n=1}^{\infty }n\cdot f_{ii}^{(n)}.

Состояние i является положительно рекуррентным (или ненулевым постоянным), если M _i конечно; в противном случае состояние i является нулевым рекуррентным (или нулевым постоянным). Положительное и нулевое повторение являются свойствами классов. ^[1]

Поглощающие государства

Состояние i называется поглощающим, если из него невозможно выйти. Следовательно, состояние i является поглощающим тогда и только тогда, когда

p_{ii}=1{\text{ and }}p_{ij}=0{\text{ for }}i\not =j.

Если каждое состояние может достичь поглощающего состояния, то цепь Маркова является поглощающей цепью Маркова . ^[4]^[5]

Обратимая цепь Маркова

Цепь Маркова называется обратимой, если существует такое распределение вероятностей $π$ по ее состояниям, что

\pi _{i}\Pr(X_{n+1}=j\mid X_{n}=i)=\pi _{j}\Pr(X_{n+1}=i\mid X_{n}=j)

для всех времен n и всех состояний i и j . Это условие известно как условие детального баланса (или уравнение локального баланса).

Учитывая фиксированное произвольное время n и используя сокращение

p_{ij}=\Pr(X_{n+1}=j\mid X_{n}=i)\,,

подробное уравнение баланса можно записать более компактно как

\pi _{i}p_{ij}=\pi _{j}p_{ji}\,.

^[1]

Один временной шаг от n до n + 1 можно рассматривать как то, что каждый человек i изначально имеет $π$ _i долларов и платит каждому человеку j долю p _ij от этой суммы. Подробное условие баланса гласит, что при каждом платеже другой человек возвращает точно такую же сумму денег. ^[6] Очевидно, что общая сумма денег $π,$ которую имеет каждый человек, остается неизменной после определенного временного шага, поскольку каждый потраченный доллар уравновешивается соответствующим полученным долларом. Более формально это можно показать равенством

\sum _{i}\pi _{i}p_{ij}=\sum _{i}\pi _{j}p_{ji}=\pi _{j}\sum _{i}p_{ji}=\pi _{j}\,,

который, по сути, гласит, что общая сумма денег, которую человек j получает (в том числе и от себя) в течение определенного периода времени, равна сумме денег, которую он платит другим, что равняется всем деньгам, которые у него были изначально, поскольку предполагалось, что все деньги потрачены (что то есть сумма p _ji равна 1 по i ). Предположение носит технический характер, поскольку деньги, которые на самом деле не используются, рассматриваются просто как выплаты от человека j самому себе (то есть p _jj не обязательно равно нулю).

Поскольку n было произвольным, это рассуждение справедливо для любого n , и, следовательно, для обратимых цепей Маркова $π$ всегда является стационарным распределением Pr( X _{n +1} = j | X _n = i ) для каждого n .

Если цепь Маркова начинается в установившемся распределении, т. е. если $\Pr(X_{0}=i)=\pi _{i}$ , затем $\Pr(X_{n}=i)=\pi _{i}$ для всех $n$ и подробное уравнение баланса можно записать как

\Pr(X_{n}=i,X_{n+1}=j)=\Pr(X_{n+1}=i,X_{n}=j)\,.

Левая и правая части этого последнего уравнения идентичны, за исключением того, что индексы времени n и n + 1 меняются местами.

Критерий Колмогорова дает необходимое и достаточное условие обратимости цепи Маркова непосредственно из вероятностей матрицы перехода. Критерий требует, чтобы произведения вероятностей вокруг каждого замкнутого контура были одинаковыми в обоих направлениях вокруг контура.

Обратимые цепи Маркова распространены в подходах Монте-Карло (MCMC) цепей Маркова, поскольку подробное уравнение баланса для желаемого распределения $π$ обязательно подразумевает, что цепь Маркова была построена так, что $π$ является устойчивым распределением. Даже в случае неоднородных во времени цепей Маркова, где используется несколько матриц перехода, если каждая такая матрица перехода демонстрирует подробный баланс с желаемым $распределением π$ , это обязательно означает, что $π$ является установившимся распределением цепи Маркова.

Ближайшая обратимая цепь Маркова

Для любой однородной по времени цепи Маркова, заданной матрицей перехода $P\in \mathbb {R} ^{n\times n}$ , любая норма $||\cdot ||$ на $\mathbb {R} ^{n\times n}$ который индуцирован скалярным произведением и любым вектором вероятности $\pi$ , существует единственная матрица перехода $P^{*}$ который является обратимым согласно $\pi$ и что ближе всего $P$ по норме $||\cdot ||.$ Матрица $P^{*}$ может быть вычислено путем решения задачи квадратично-выпуклой оптимизации. ^[7]

Например, рассмотрим следующую цепь Маркова:

Эта цепь Маркова не обратима. По норме Фробениуса ближайшая обратимая цепь Маркова по $\pi =\left({\frac {1}{3}},{\frac {1}{3}},{\frac {1}{3}}\right)$ может быть вычислено как

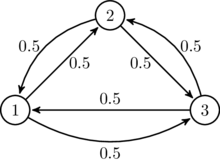
Если мы выберем вектор вероятности случайным образом как $\pi =\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{2}}\right)$ , то ближайшая обратимая цепь Маркова по норме Фробениуса приближенно имеет вид

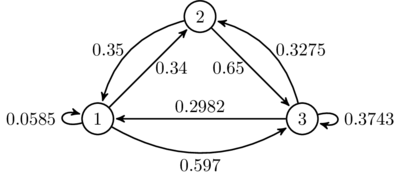
Стационарные распределения

Распределение $\pi$ представляет собой стационарное распределение цепи Маркова со стохастической матрицей $P$ тогда и только тогда, когда $\pi P=\pi$ . Это можно записать как: ^[1]

\forall j\in \mathbb {S} :\sum _{i\in \mathbb {S} }\pi _{i}p_{ij}=\pi _{j}

.

Это условие подразумевает, что $\pi P^{n}=\pi$ и, следовательно, если цепь Маркова $(X_{n},n\in \mathbb {N} )$ имеет начальное распространение $X_{0}=\pi$ затем $X_{n}=\pi$ (в раздаче) для любого $n\in \mathbb {N}$ . ^[1]

Если цепь Маркова неприводима, то она имеет стационарное распределение тогда и только тогда, когда она положительно рекуррентна, ^[8] в этом случае уникальное такое распределение определяется выражением $\pi _{i}={\frac {1}{M_{i}}}$ где $M_{i}=\mathbb {E} (T_{i})$ среднее время повторения i . ^[1]

Если в цепочке имеется более одного закрытого взаимодействующего класса, ее стационарные распределения не будут уникальными (рассмотрим любой замкнутый взаимодействующий класс $C_{i}$ в цепочке; у каждого будет свое уникальное стационарное распределение $\pi _{i}$ . Распространение этих распределений на всю цепочку, приравнивая к нулю все значения вне класса связи, приводит к тому, что набор инвариантных мер исходной цепочки представляет собой набор всех выпуклых комбинаций $\pi _{i}$ х). Однако если состояние j апериодично, то $\lim \nolimits _{n\rightarrow \infty }p_{jj}^{(n)}={\tfrac {C}{M_{j}}}$ и для любого другого состояния i пусть f _ij будет вероятностью того, что цепочка когда-либо посетит состояние j, если оно начинается с i , $\lim \nolimits _{n\rightarrow \infty }p_{ij}^{(n)}=C{\tfrac {f_{ij}}{M_{j}}}.$

Если состояние i периодично с периодом k > 1, то предел $\lim \nolimits _{n\rightarrow \infty }p_{ii}^{(n)}$ не существует, хотя предел $\lim \nolimits _{n\rightarrow \infty }p_{ii}^{(kn+r)}$ существует для каждого целого числа r .

Стационарный анализ и неоднородная во времени цепь Маркова

Цепь Маркова не обязательно должна быть однородной во времени, чтобы иметь равновесное распределение. Если существует распределение вероятностей по состояниям ${\boldsymbol {\pi }}$ такой, что

\pi _{j}=\sum _{i\in S}\pi _{i}\,\Pr(X_{n+1}=j\mid X_{n}=i)

для каждого состояния j и каждый раз n тогда ${\boldsymbol {\pi }}$ является равновесным распределением цепи Маркова. Такое может произойти в методах Монте-Карло с цепями Маркова (MCMC) в ситуациях, когда используется несколько различных матриц перехода, поскольку каждая из них эффективна для определенного типа смешивания, но каждая матрица соответствует общему равновесному распределению.

Время ударов

Время попадания — это время, начиная с данного набора состояний и до тех пор, пока цепочка не достигнет данного состояния или набора состояний. Распределение такого периода времени имеет распределение фазового типа. Простейшим таким распределением является распределение одного экспоненциально распределенного перехода. ^{[ нужна ссылка ]}

Ожидаемое время попадания

Для подмножества состояний A ⊆ S вектор k ^А времени попадания (где элемент $k_{i}^{A}$ представляет собой ожидаемое значение , начиная с состояния i , в котором цепочка входит в одно из состояний множества A ) является минимальным неотрицательным решением ^[9]

{\begin{aligned}k_{i}^{A}=0&{\text{ for }}i\in A\\-\sum _{j\in S}q_{ij}k_{j}^{A}=1&{\text{ for }}i\notin A.\end{aligned}}

Эргодическая теорема

Пример эргодической теории , эргодическая теорема для состояний, которая для неприводимой апериодической цепи Маркова для любых двух состояний i и j , ^[1]

p_{i,j}^{(n)}\rightarrow {\frac {1}{M_{j}}}

как

n\rightarrow \infty

.

Примечания

^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п Гриметт, Греция ; Стирзакер, Д.Р. (1992). «6». Вероятность и случайные процессы (второе изд.). Издательство Оксфордского университета. ISBN 0198572220 .
^ Ашер Левин, Дэвид (2009). Цепи Маркова и времена смешивания . п. 16 . ISBN 978-0-8218-4739-8 .
^ Лоулер, Грегори Ф. (2006). Введение в случайные процессы (2-е изд.). ЦРК Пресс. ISBN 1-58488-651-Х .
^ Гринстед, Чарльз М.; Снелл, Дж. Лори (июль 1997 г.). «Глава 11: Цепи Маркова» (PDF) . Введение в вероятность . Американское математическое общество. ISBN 978-0-8218-0749-1 .
^ Кемени, Джон Г .; Снелл, Дж. Лори (июль 1976 г.) [1960]. «Глава 3: Поглощающие цепи Маркова». В Геринге, ФРВ; Халмош, PR (ред.). Конечные цепи Маркова (второе изд.). Нью-Йорк Берлин Гейдельберг Токио: Springer-Verlag. стр. 224 . ISBN 978-0-387-90192-3 .
^ Ричард Дарретт (19 мая 2012 г.). Основы случайных процессов . Springer Science & Business Media. п. 37. ИСБН 978-1-4614-3615-7 . Архивировано из оригинала 6 февраля 2017 года.
^ А. Нильсен, М. Вебер. Интернет-публикация в журнале «Численная линейная алгебра с приложениями», DOI: 10.1002/nla.1967, 2015.
^ Серфозо, Ричард (2009), «Основы прикладных случайных процессов» , Вероятность и ее приложения : 35, doi : 10.1007/978-3-540-89332-5 , ISBN 978-3-540-89331-8 , MR 2484222 , заархивировано из оригинала 19 марта 2015 г.
^ Норрис, младший (1997). «Цепи Маркова в непрерывном времени II». Марковские цепи . стр. 108–127. дои : 10.1017/CBO9780511810633.005 . ISBN 9780511810633 .

Ссылки

А. А. Марков (1971). «Распространение предельных теорем теории вероятностей на сумму переменных, связанных в цепочку». перепечатано в Приложении B: Р. Ховард. Динамические вероятностные системы, том 1: Цепи Маркова . Джон Уайли и сыновья.
Марков А.А. (2006). «Пример статистического исследования текста «Евгений Онегин» по поводу соединения образцов в цепочки». Наука в контексте . 19 (4). Перевод Линка, Дэвид: 591–600. дои : 10.1017/s0269889706001074 . S2CID 144854176 .
Лео Брейман (1992) [1968] Вероятность . Оригинальное издание опубликовано Аддисон-Уэсли; перепечатано Обществом промышленной и прикладной математики. ISBN 0-89871-296-3 . (См. главу 7)
Дж. Л. Дуб (1953) Стохастические процессы . Нью-Йорк: Джон Уайли и сыновья ISBN 0-471-52369-0 .
С. П. Мейн и Р. Л. Твиди (1993) Марковские цепи и стохастическая устойчивость . Лондон: Спрингер-Верлаг ISBN 0-387-19832-6 . онлайн: МЦСС . Появится второе издание, Cambridge University Press, 2009 г.
Кемени, Джон Г.; Хэзлтон Миркил; Дж. Лори Снелл; Джеральд Л. Томпсон (1959). Конечные математические структуры (1-е изд.). Энглвуд Клиффс, Нью-Джерси: Prentice-Hall, Inc. Номер карточного каталога Библиотеки Конгресса 59-12841. Классический текст. см. главу 6. Конечные цепи Маркова, стр. 384 и далее.
Джон Г. Кемени и Дж. Лори Снелл (1960) Конечные цепи Маркова , компания Д. ван Ностранда ISBN 0-442-04328-7
Э. Нуммелин. «Общие неприводимые цепи Маркова и неотрицательные операторы». Издательство Кембриджского университета, 1984, 2004. ISBN 0-521-60494-X
Сенета, Э. Неотрицательные матрицы и цепи Маркова . 2-я ред. изд., 1981, XVI, 288 стр., Серия Springer в мягкой обложке по статистике. (Первоначально опубликовано Allen & Unwin Ltd., Лондон, 1973 г.) ISBN 978-0-387-29765-1

[PRS-1] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п Гриметт, Греция ; Стирзакер, Д.Р. (1992). «6». Вероятность и случайные процессы (второе изд.). Издательство Оксфордского университета. ISBN 0198572220 .

[2] Ашер Левин, Дэвид (2009). Цепи Маркова и времена смешивания . п. 16 . ISBN 978-0-8218-4739-8 .

[Lawler-3] Лоулер, Грегори Ф. (2006). Введение в случайные процессы (2-е изд.). ЦРК Пресс. ISBN 1-58488-651-Х .

[Grin-4] Гринстед, Чарльз М.; Снелл, Дж. Лори (июль 1997 г.). «Глава 11: Цепи Маркова» (PDF) . Введение в вероятность . Американское математическое общество. ISBN 978-0-8218-0749-1 .

[Kem-5] Кемени, Джон Г .; Снелл, Дж. Лори (июль 1976 г.) [1960]. «Глава 3: Поглощающие цепи Маркова». В Геринге, ФРВ; Халмош, PR (ред.). Конечные цепи Маркова (второе изд.). Нью-Йорк Берлин Гейдельберг Токио: Springer-Verlag. стр. 224 . ISBN 978-0-387-90192-3 .

[Durrett2012-6] Ричард Дарретт (19 мая 2012 г.). Основы случайных процессов . Springer Science & Business Media. п. 37. ИСБН 978-1-4614-3615-7 . Архивировано из оригинала 6 февраля 2017 года.

[7] А. Нильсен, М. Вебер. Интернет-публикация в журнале «Численная линейная алгебра с приложениями», DOI: 10.1002/nla.1967, 2015.

[8] Серфозо, Ричард (2009), «Основы прикладных случайных процессов» , Вероятность и ее приложения : 35, doi : 10.1007/978-3-540-89332-5 , ISBN 978-3-540-89331-8 , MR 2484222 , заархивировано из оригинала 19 марта 2015 г.

[norris2-9] Норрис, младший (1997). «Цепи Маркова в непрерывном времени II». Марковские цепи . стр. 108–127. дои : 10.1017/CBO9780511810633.005 . ISBN 9780511810633 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]