Поглощающая цепь Маркова

В математической теории вероятностей поглощающая цепь Маркова — это цепь Маркова , в которой каждое состояние может достичь поглощающего состояния. Поглощающее состояние – это состояние, из которого, попав в него, невозможно выйти.

Как и общие цепи Маркова, могут существовать поглощающие цепи Маркова с непрерывным временем и бесконечным пространством состояний. Однако эта статья концентрируется на случае дискретного пространства состояний с дискретным временем.

Формальное определение

Цепь Маркова является поглощающей цепью, если ^[1]^[2]

существует хотя бы одно поглощающее состояние и
из любого состояния можно перейти хотя бы в одно поглощающее состояние за конечное число шагов.

В поглощающей цепи Маркова состояние, которое не является поглощающим, называется переходным.

Каноническая форма

Пусть поглощающая цепь Маркова с матрицей перехода P имеет t переходных состояний и r поглощающих состояний. В отличие от типичной матрицы перехода, строки P представляют источники, а столбцы представляют пункты назначения. Затем

P={\begin{bmatrix}Q&R\\\mathbf {0} &I_{r}\end{bmatrix}},

где Q — матрица t -x -t , R — ненулевая матрица t -x -r , 0 — нулевая матрица r -x- t , а I _r — r -x- r единичная матрица . Таким образом, Q описывает вероятность перехода из одного переходного состояния в другое, а R описывает вероятность перехода из некоторого переходного состояния в некоторое поглощающее состояние.

Вероятность перехода от i к j ровно за k шагов — это ( i , j )-запись P ^к, дальнейшее вычисление ниже. При рассмотрении только переходных состояний вероятность, найденная в левом верхнем углу P ^к, ( i , j )-запись Q ^к.

Фундаментальная матрица

Ожидаемое количество посещений переходного состояния

Основным свойством поглощающей цепи Маркова является ожидаемое количество посещений переходного состояния j, начиная с переходного состояния i (до поглощения). Можно установить, что это задается записью ( i , j ) так называемой фундаментальной матрицы N , полученной суммированием Q ^к для всех k (от 0 до ∞). Можно доказать, что

N:=\sum _{k=0}^{\infty }Q^{k}=(I_{t}-Q)^{-1},

где I _t — единичная матрица t -by -t . Вычисление этой формулы является матричным эквивалентом геометрической прогрессии скаляров: ${\textstyle \sum }_{k=0}^{\infty }q^{k}={\tfrac {1}{1-q}}$ .

Имея под рукой матрицу N , легко получить и другие свойства цепи Маркова. ^[2]

Ожидаемое количество шагов до поглощения

Ожидаемое количество шагов до поглощения в любом поглощающем состоянии при запуске в переходном состоянии i можно вычислить посредством суммы по переходным состояниям. Значение задается i- й записью вектора

\mathbf {t} :=N\mathbf {1} ,

где 1 — вектор-столбец длины t , все элементы которого равны 1.

Поглощение вероятностей

По индукции

P^{k}={\begin{bmatrix}Q^{k}&(1-Q^{k})NR\\\mathbf {0} &I_{r}\end{bmatrix}}.

Вероятность того, что в конечном итоге будет поглощено поглощающим состоянием j при старте из переходного состояния i, определяется ( i , j )-записью матрицы

B:=NR

.

Число столбцов этой матрицы равно числу поглощающих состояний r .

Аппроксимацию этих вероятностей можно также получить непосредственно из ( i , j )-записи $P^{k}$ для достаточно большого значения k , когда i — индекс переходного процесса, а j — индекс поглощающего состояния. Это потому, что

\left(\lim _{k\to \infty }P^{k}\right)_{i,t+j}=B_{i,j}

.

Вероятность временного посещения

Вероятность посещения переходного состояния j при старте из переходного состояния i - это ( i , j )-запись матрицы

H:=(N-I_{t})(N_{\operatorname {dg} })^{-1},

где N _dg — диагональная матрица с той же диагональю, что N. и

Разница в количестве временных посещений

Дисперсия количества посещений переходного состояния j с началом переходного состояния i (до поглощения) представляет собой ( i , j )-запись матрицы

N_{2}:=N(2N_{\operatorname {dg} }-I_{t})-N_{\operatorname {sq} },

где N _sq — Адамара произведение N на самого себя (т.е. каждая запись N возведена в квадрат).

Разница в количестве шагов

Отклонение количества шагов до поглощения при запуске в переходном состоянии i - это i -я запись вектора.

(2N-I_{t})\mathbf {t} -\mathbf {t} _{\operatorname {sq} },

где t _sq — произведение Адамара на t самого себя (т.е., как и в случае с N _sq , каждая запись t возводится в квадрат).

Примеры

Генерация строк

Рассмотрим процесс многократного подбрасывания честной монеты до тех пор, пока не появится последовательность (орёл, решка, орёл). Этот процесс моделируется поглощающей цепью Маркова с матрицей перехода

P={\begin{bmatrix}1/2&1/2&0&0\\0&1/2&1/2&0\\1/2&0&0&1/2\\0&0&0&1\end{bmatrix}}.

Первое состояние представляет пустую строку , второе состояние — строку «H», третье — строку «HT», а четвертое — строку «HTH». Хотя на самом деле подбрасывание монеты прекращается после генерации строки «HTH», перспектива поглощающей цепи Маркова заключается в том, что процесс перешел в поглощающее состояние, представляющее строку «HTH», и, следовательно, не может выйти.

Для этой поглощающей цепи Маркова фундаментальная матрица имеет вид

{\begin{aligned}N&=(I-Q)^{-1}=\left({\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}-{\begin{bmatrix}1/2&1/2&0\\0&1/2&1/2\\1/2&0&0\end{bmatrix}}\right)^{-1}\\[4pt]&={\begin{bmatrix}1/2&-1/2&0\\0&1/2&-1/2\\-1/2&0&1\end{bmatrix}}^{-1}={\begin{bmatrix}4&4&2\\2&4&2\\2&2&2\end{bmatrix}}.\end{aligned}}

Ожидаемое количество шагов, начиная с каждого из переходных состояний, равно

\mathbf {t} =N\mathbf {1} ={\begin{bmatrix}4&4&2\\2&4&2\\2&2&2\end{bmatrix}}{\begin{bmatrix}1\\1\\1\end{bmatrix}}={\begin{bmatrix}10\\8\\6\end{bmatrix}}.

Следовательно, ожидаемое количество подбрасываний монеты до наблюдения за последовательностью (орёл, решка, орёл) равно 10, что соответствует состоянию, представляющему пустую строку.

Азартные игры

Игры, полностью основанные на случайности, можно смоделировать с помощью поглощающей цепи Маркова. Классическим примером этого является древнеиндийская настольная игра « Змеи и лестницы» . График слева ^[3] отображает вероятностную массу в одиночном поглощающем состоянии, которое представляет собой последний квадрат, когда матрица перехода возводится во все большие и большие степени. Чтобы определить ожидаемое количество ходов для завершения игры, вычислите вектор t, как описано выше, и проверьте t _start , который равен примерно 39,2.

Тестирование на инфекционные заболевания

Тестирование на инфекционные заболевания, как препаратов крови, так и в медицинских клиниках, часто преподается как пример поглощающей цепи Маркова. ^[4] Например, общественная модель Центров по контролю и профилактике заболеваний США (CDC) для ВИЧ и гепатита B: ^[5] иллюстрирует свойство, заключающееся в том, что поглощение цепей Маркова может привести к обнаружению заболевания по сравнению с потерей обнаружения другими способами.

В стандартной модели CDC цепь Маркова имеет пять состояний: состояние, в котором человек не инфицирован, затем состояние с инфицированным, но необнаружимым вирусом, состояние с обнаруживаемым вирусом и поглощающие состояния выхода из клиники/выхода из клиники. или быть обнаруженным (цель). Типичными скоростями перехода между марковскими состояниями являются вероятность p в единицу времени заражения вирусом, w для скорости удаления периода окна (время до обнаружения вируса), q для скорости выхода/потери из системы и d для обнаружения, предполагая типичную скорость $\lambda$ во время которого система здравоохранения проводит тесты препарата крови или пациентов, о которых идет речь.

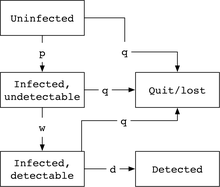
Классический пример модели скрининга вируса ВИЧ или гепатита

Отсюда следует, что мы можем «пройтись» по модели Маркова, чтобы определить общую вероятность обнаружения человека, начинающегося как необнаруженный, путем умножения вероятностей перехода в каждое следующее состояние модели как:

${\frac {p}{(p+q)}}{\frac {w}{(w+q)}}{\frac {d}{(d+q)}}$ .

Последующее общее абсолютное количество ложноотрицательных тестов (основная проблема Центров по контролю и профилактике заболеваний) будет тогда равно количеству тестов, умноженному на вероятность достижения инфицированного, но необнаружимого состояния, умноженному на продолжительность пребывания в инфицированном необнаружимом состоянии:

${\frac {p}{(p+q)}}{\frac {1}{(w+q)}}\lambda$ .

См. также

Ссылки

^ Jump up to: ^а ^б Гринстед, Чарльз М.; Снелл, Дж. Лори (июль 1997 г.). «Глава 11: Цепи Маркова» (PDF) . Введение в вероятность . Американское математическое общество. ISBN 978-0-8218-0749-1 .
^ Jump up to: ^а ^б Кемени, Джон Г .; Снелл, Дж. Лори (июль 1976 г.) [1960]. «Гл. 3: Поглощающие цепи Маркова». В Геринге, ФРВ; Халмош, PR (ред.). Конечные цепи Маркова (второе изд.). Нью-Йорк Берлин Гейдельберг Токио: Springer-Verlag. стр. 224 . ISBN 978-0-387-90192-3 .
^ На основе определения, найденного в СК Альтхен; Л. Кинг; К. Шиллинг (март 1993 г.). «Как долго длится игра в змеи и лестницы?». Математический вестник . 78 (478). Математический вестник, Vol. 77, № 478: 71–76. дои : 10.2307/3619261 . JSTOR 3619261 .
^ результаты, поиск (28 июля 1998 г.). Марковские цепи . Кембридж: Издательство Кембриджского университета. ISBN 9780521633963 .
^ Сандерс, Джиллиан Д.; Анайя, Генри Д.; Аш, Стивен; Хоанг, Туен; Голден, Джоя Ф.; Баюми, Ахмед М.; Оуэнс, Дуглас К. (июнь 2010 г.). «Экономическая эффективность стратегий по улучшению тестирования на ВИЧ и получения результатов: экономический анализ рандомизированного контролируемого исследования» . Журнал общей внутренней медицины . 25 (6): 556–563. дои : 10.1007/s11606-010-1265-5 . ISSN 0884-8734 . ПМК 2869414 . ПМИД 20204538 .

Внешние ссылки

[Grin-1] Jump up to: ^а ^б Гринстед, Чарльз М.; Снелл, Дж. Лори (июль 1997 г.). «Глава 11: Цепи Маркова» (PDF) . Введение в вероятность . Американское математическое общество. ISBN 978-0-8218-0749-1 .

[Kem-2] Jump up to: ^а ^б Кемени, Джон Г .; Снелл, Дж. Лори (июль 1976 г.) [1960]. «Гл. 3: Поглощающие цепи Маркова». В Геринге, ФРВ; Халмош, PR (ред.). Конечные цепи Маркова (второе изд.). Нью-Йорк Берлин Гейдельберг Токио: Springer-Verlag. стр. 224 . ISBN 978-0-387-90192-3 .

[3] На основе определения, найденного в СК Альтхен; Л. Кинг; К. Шиллинг (март 1993 г.). «Как долго длится игра в змеи и лестницы?». Математический вестник . 78 (478). Математический вестник, Vol. 77, № 478: 71–76. дои : 10.2307/3619261 . JSTOR 3619261 .

[4] результаты, поиск (28 июля 1998 г.). Марковские цепи . Кембридж: Издательство Кембриджского университета. ISBN 9780521633963 .

[5] Сандерс, Джиллиан Д.; Анайя, Генри Д.; Аш, Стивен; Хоанг, Туен; Голден, Джоя Ф.; Баюми, Ахмед М.; Оуэнс, Дуглас К. (июнь 2010 г.). «Экономическая эффективность стратегий по улучшению тестирования на ВИЧ и получения результатов: экономический анализ рандомизированного контролируемого исследования» . Журнал общей внутренней медицины . 25 (6): 556–563. дои : 10.1007/s11606-010-1265-5 . ISSN 0884-8734 . ПМК 2869414 . ПМИД 20204538 .

[1]

[2]

[3]

[4]

[5]