Сферический сегмент
Эта статья включает список литературы , связанную литературу или внешние ссылки , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . ( Май 2024 г. ) |



В геометрии сферический сегмент — это твердое тело, определяемое разрезанием сферы или шара парой параллельных плоскостей .Его можно представить как сферическую шапку с усеченной вершиной, поэтому она соответствует усеченной сфере .
Поверхность сегмента сферического сферической (без учета оснований) называется зоной .
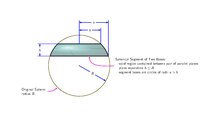
Если радиус сферы называется R , радиусы оснований сферического сегмента — a и b , а высота сегмента (расстояние от одной параллельной плоскости до другой) — h , то объем сферического сегмента равен
Для частного случая, когда верхняя плоскость касается сферы, мы имеем и твердое тело превращается в сферическую шапку . [1]
Приведенное выше уравнение для объема сферического сегмента можно записать так:
Таким образом, объем сегмента равен сумме трех объемов: двух прямых круговых цилиндров, один радиуса a , второй радиуса b (оба высотой ) и сфера радиуса .
Площадь изогнутой поверхности сферической зоны, исключая верхнее и нижнее основания, определяется выражением
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Керн, Уиллис; Бланд, Джеймс (1938). Твердые измерения с доказательствами (второе изд.). Нью-Йорк: John Wiley & Sons, Inc., стр. 97–103 . Проверено 16 мая 2024 г.
- Керн, Уильям Ф.; Бланд, Джеймс Р. (1938). Твердые измерения с доказательствами . п. 95–97 .
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Сферический сегмент» . Математический мир .
- Вайсштейн, Эрик В. «Сферическая зона» . Математический мир .
- Краткое изложение сферических формул


![{\displaystyle V={\biggl [}\pi a^{2}\left({\frac {h}{2}}{\biggr)}\right]+{\biggl [}\pi b^{2 }\left({\frac {h}{2}}{\biggr )}\right]+{\biggl [}{\frac {4}{3}}\pi \left({\frac {h}{ 2}}\right)^{3}{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7471ad7473b6909c362fb97c9fd839ac4d0f7b1)

