Пространственная неоднородность
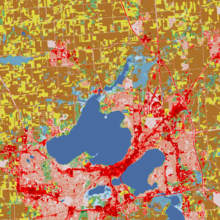
Пространственная неоднородность — это свойство, обычно приписываемое ландшафту или населению . Это относится к неравномерному распределению различных концентраций каждого вида на территории. Ландшафт с пространственной неоднородностью представляет собой сочетание концентраций нескольких видов растений или животных (биологических), или образований местности (геологических), или характеристик окружающей среды (например, осадков, температуры, ветра), заполняющих его территорию. Популяция, демонстрирующая пространственную неоднородность, — это популяция, в которой различные концентрации особей этого вида распределены по территории неравномерно; почти синоним слова «неравномерно распределенный».
Терминология
[ редактировать ]Пространственную неоднородность можно перефразировать как масштабную иерархию гораздо большего количества мелких вещей, чем крупных. Он был сформулирован как закон масштабирования. [1]
Пространственная неоднородность или иерархия масштабирования могут быть измерены или количественно определены с помощью ht-index : числа, вызванного разрывами головы/хвоста . [2] [3]
Примеры
[ редактировать ]Окружающая среда с большим разнообразием сред обитания, таких как различная топография , типы почв и климат, способна вместить большее количество видов . Ведущее научное объяснение этому состоит в том, что, когда организмы могут точно разделить ландшафт на уникальные подходящие среды обитания, больше видов могут сосуществовать в ландшафте без конкуренции - явление, называемое «разделением ниши». Пространственная неоднородность – понятие, параллельное продуктивности экосистемы , видовое богатство животных напрямую связано с видовым богатством растений в определенном ареале. Растительность служит источником пищи, средой обитания и так далее. Следовательно, если растительности мало, популяция животных тоже будет. Чем больше видов растений присутствует в экосистеме, тем больше разнообразие микросред обитания. Богатство видов растений напрямую отражает пространственную неоднородность экосистемы.
Типы
[ редактировать ]Существуют два основных типа пространственной неоднородности. Пространственная локальная неоднородность классифицирует географические явления, значения атрибутов которых значительно схожи в пределах непосредственно локальной окрестности, но которые значительно различаются в близлежащих районах за пределами этой непосредственно локальной окрестности (например, горячие точки, холодные точки). Пространственная стратифицированная неоднородность классифицирует географические явления, у которых внутри слоев дисперсия значений атрибутов значительно ниже, чем их дисперсия между слоями, например, наборы экологических зон или классов землепользования в пределах данной географической области. [4]
Тестирование
[ редактировать ]Пространственную локальную неоднородность можно проверить с помощью LISA, Gi и SatScan, а пространственную стратифицированную неоднородность атрибута можно измерить с помощью географического детектора q -статистики: [4]
где популяция разбита на h = 1, ..., L страты; N обозначает размер популяции, σ 2 означает дисперсию атрибута. Значение q находится в пределах [0, 1], 0 указывает на отсутствие пространственной стратифицированной неоднородности, 1 указывает на идеальную пространственную стратифицированную неоднородность. Значение q указывает процент дисперсии атрибута, объясняемый стратификацией. q F. соответствует нецентральной функции плотности вероятности

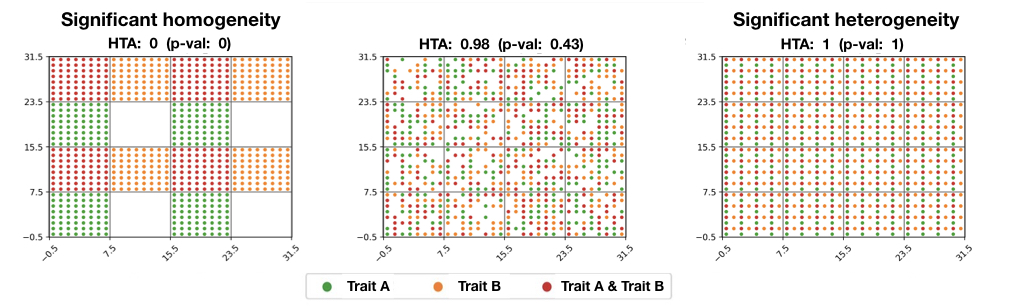
Пространственную неоднородность многомерных данных и 3D-данных также можно оценить статистически с помощью «Индекс HTA (средний индекс гетерогенности)» . : [5]
Модели
[ редактировать ]Пространственная стратифицированная неоднородность
[ редактировать ]Географический детектор на основе оптимальных параметров
[ редактировать ]Географический детектор на основе оптимальных параметров (OPGD) характеризует пространственную неоднородность с помощью оптимизированных параметров дискретизации пространственных данных для выявления географических факторов и интерактивного воздействия факторов, а также оценки рисков. [6] [7]
Интерактивный детектор пространственных ассоциаций
[ редактировать ]Интерактивный детектор пространственных ассоциаций (IDSA) оценивает мощность интерактивных определителей (PID) на основе пространственной стратифицированной неоднородности, пространственной автокорреляции и пространственного нечеткого наложения объясняющих переменных. [8]
Географически оптимальная неоднородность на основе зон
[ редактировать ]Гетерогенность на основе географически оптимальных зон (GOZH) исследует отдельные и интерактивные детерминанты географических атрибутов (например, глобальную влажность почвы) на большой территории исследования на основе выявления объяснимых географически оптимальных зон. [9]
Надежный географический детектор
[ редактировать ]Робастный географический детектор (RGD) преодолевает ограничение чувствительности при дискретизации пространственных данных и оценивает робастную мощность определителей объясняющих переменных. [10]
мета-ЗВЕЗДА
[ редактировать ]Независимая от модели пространственная трансформация и режим (meta-STAR) представляет собой основу для интеграции пространственной неоднородности в пространственные статистические модели (например, методы пространственного ансамбля, пространственные нейронные сети) с целью повышения их точности. Он предполагает использование пространственных сетей/преобразований и пространственных модераторов , а также обрабатывает наборы геопространственных данных, представляющие географические явления в различных масштабах. [11]
Закон географии
[ редактировать ]В публикации 2004 года под названием «Действительность и полезность законов в географической информатике и географии» Майкл Фрэнк Гудчайлд предположил, что пространственная неоднородность может быть кандидатом на роль закона географии, аналогичного первому закону географии Тоблера . [12] В литературе цитируется эта статья и утверждается, что этот закон «географические переменные демонстрируют неконтролируемую дисперсию». [12] [13] [14] Часто называемый вторым законом географии или вторым законом географии Майкла Гудчайлда, это одна из многих концепций, конкурирующих за этот термин, включая второй закон географии Тоблера и закон географии Арбиа . [13] [14] [15]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Цзян Б. 2015. Геопространственный анализ требует другого образа мышления: проблема пространственной неоднородности. Геожурнал 80 (1), 1–13.
- ^ Цзян Б. и Инь Дж. 2014. Ht-индекс для количественной оценки фрактальной или масштабной структуры географических объектов, Анналы Ассоциации американских географов, 104 (3), 530–541.
- ^ Цзян Б. 2013. Разрывы головы и хвоста: новая схема классификации данных с распределением с тяжелым хвостом, The Professional Geographer, 65 (3), 482–494.
- ^ Jump up to: а б Ван Дж.Ф., Чжан Т.Л., Фу Б.Дж. 2016. Мера пространственной стратифицированной неоднородности. Экологические показатели 67: 250-256.
- ^ Jump up to: а б Алона Леви-Юргенсон и другие, Оценка гетерогенности пространственных данных с использованием индекса HTA с применением к пространственной транскриптомике и визуализации, Биоинформатика, том 37, выпуск 21, ноябрь 2021 г., страницы 3796–3804, https://doi.org/10.1093/ биоинформатика/btab569
- ^ Сун, Юнцзе; Ван, Цзиньфэн; Ге, Юн; Сюй, Чэндун (2020). «Модель географического детектора на основе оптимальных параметров расширяет географические характеристики объясняющих переменных для анализа пространственной неоднородности: случаи с различными типами пространственных данных» . ГИС-науки и дистанционное зондирование . 57 (5): 593–610. дои : 10.1080/15481603.2020.1760434 . hdl : 20.500.11937/79549 . ISSN 1548-1603 . S2CID 219418482 .
- ^ Сун, Юнцзе (2021). «Модель географических детекторов на основе оптимальных параметров (OPGD) для анализа пространственной неоднородности и исследования факторов» .
- ^ Сун, Юнцзе; Ву, Пэн (2021). «Интерактивный детектор пространственных ассоциаций» . Международный журнал географической информатики . 35 (8): 1676–1701. дои : 10.1080/13658816.2021.1882680 . ISSN 1365-8816 . S2CID 234812819 .
- ^ Ло, Пэн; Сун, Юнцзе; Хуан, Синь; Ма, Хунлян; Лю, Цзинь; Яо, Яо; Мэн, Лицю (2022). «Выявление факторов, определяющих пространственно-временные различия во влажности почвы Северного полушария с использованием географически оптимальной зональной модели неоднородности» . Журнал фотограмметрии и дистанционного зондирования ISPRS . 185 : 111–128. Бибкод : 2022JPRS..185..111L . дои : 10.1016/j.isprsjprs.2022.01.009 . S2CID 246496936 .
- ^ Чжан, Цзэхуа; Сун, Юнцзе; Ву, Пэн (2022). «Надежный географический детектор» . Международный журнал прикладного наблюдения Земли и геоинформации . 109 : 102782. дои : 10.1016/j.jag.2022.102782 . hdl : 20.500.11937/88650 . S2CID 248470509 .
- ^ Се Ю, Чен В, Хэ Э, Цзя Икс, Бао Х, Чжоу Икс, Гош Р, Равиратинам П (2023). «Использование неоднородности в пространстве с помощью статистически управляемого метаобучения» . Знания и информационные системы . 65 (6): 2699–2729. дои : 10.1007/s10115-023-01847-0 . ПМЦ 9994417 . ПМИД 37035130 .
- ^ Jump up to: а б Гудчайлд, Майкл (2004). «Действительность и полезность законов в географической информатике и географии». Анналы Ассоциации американских географов . 94 (2): 300–303. дои : 10.1111/j.1467-8306.2004.09402008.x . S2CID 17912938 .
- ^ Jump up to: а б Цзоу, Муцюань; Ван, Лижэнь; Ву, Пин; Тран, Ванья (23 июля 2022 г.). «Модели совместного размещения типа β для определения централизации близости в наборах пространственных данных» . ISPRS Int. Дж. Гео-Инф . 11 (8): 418. doi : 10.3390/ijgi11080418 .
- ^ Jump up to: а б Чжан, Ю; Шэн, Ву; Чжао, Чжиюань; Ян, Сипин; Фан, Чжисян (30 января 2023 г.). «Модель городского потока толпы, объединяющая географические характеристики» . Научные отчеты . 13 . дои : 10.1038/s41598-023-29000-5 . ПМЦ 9886992 .
- ^ Тоблер, Уолдо (2004). «О первом законе географии: ответ» . Анналы Ассоциации американских географов . 94 (2): 304–310. дои : 10.1111/j.1467-8306.2004.09402009.x . S2CID 33201684 . Проверено 10 марта 2022 г.
