Контекстно-свободная грамматика
Эта статья нуждается в дополнительных цитатах для проверки . ( февраль 2012 г. ) |
В формального языка теории контекстно-свободная грамматика ( CFG ) — это формальная грамматика которой , правила производства может применяться к нетерминальному символу независимо от его контекста.В частности, в контекстно-свободной грамматике каждое продукционное правило имеет вид
с одиночный нетерминальный символ и строка терминалов и/или нетерминалов ( может быть пустым). Независимо от того, какие символы его окружают, единственный нетерминал слева всегда можно заменить на с правой стороны. Это отличает ее от контекстно-зависимой грамматики , которая может иметь правила продукции в виде с нетерминальный символ и , , и строки терминальных и/или нетерминальных символов.
Формальная грамматика — это, по сути, набор правил производства, которые описывают все возможные строки на данном формальном языке. Правила производства — это простые замены. Например, первое правило на картинке,
заменяет с . Для данного нетерминального символа может существовать несколько правил замены. Язык, порожденный грамматикой, представляет собой набор всех строк терминальных символов, которые могут быть получены путем повторного применения правил из некоторого конкретного нетерминального символа («начального символа»).Нетерминальные символы используются в процессе деривации, но не появляются в окончательной строке результата.
Языки, созданные с помощью контекстно-свободных грамматик, известны как контекстно-свободные языки (CFL). Различные контекстно-свободные грамматики могут создавать один и тот же контекстно-свободный язык. Важно отличать свойства языка (внутренние свойства) от свойств конкретной грамматики (внешние свойства). Вопрос о языковом равенстве (генерируют ли две заданные контекстно-свободные грамматики один и тот же язык?) неразрешим .
Контекстно-свободные грамматики возникают в лингвистике , где они используются для описания структуры предложений и слов естественного языка они были изобретены лингвистом Ноамом Хомским , и для этой цели . Напротив, в информатике по мере увеличения использования рекурсивно определенных понятий они использовались все больше и больше. В ранних приложениях грамматики использовались для описания структуры языков программирования . В более новом приложении они используются в важной части расширяемого языка разметки (XML), называемой определением типа документа . [2]
В лингвистике некоторые авторы используют термин «грамматика фразовой структуры» для обозначения контекстно-свободных грамматик, при этом грамматики фразовой структуры отличаются от грамматик зависимостей . В информатике популярным обозначением контекстно-свободных грамматик является форма Бэкуса-Наура , или BNF.
Фон
[ редактировать ]По крайней мере, со времен древнеиндийского ученого Панини лингвисты описывали грамматики языков с точки зрения их блочной структуры и описывали, как предложения рекурсивно строятся из более мелких фраз и, в конечном итоге, из отдельных слов или элементов слов. Важным свойством этих блочных структур является то, что логические единицы никогда не перекрываются. Например, предложение:
- Джон, чья синяя машина стояла в гараже, пошел в продуктовый магазин.
может быть заключен в логические скобки (с логическими метасимволами [ ] ) следующим образом:
- [ Джон [ , [ чья [ синяя машина ]] [ была [ в [ гараже ]]] , ]] [ шла [ в [ ] ] продуктовый магазин ]] .
Контекстно-свободная грамматика обеспечивает простой и математически точный механизм для описания методов, с помощью которых фразы в некотором естественном языке строятся из более мелких блоков, естественным образом фиксируя «блочную структуру» предложений. Его простота делает формализм поддающимся строгому математическому исследованию. Важные особенности синтаксиса естественного языка, такие как согласие и ссылка, являются не частью контекстно-свободной грамматики, а базовой рекурсивной структурой предложений, способом вложения предложений в другие предложения и способом составления списков прилагательных и наречий. проглоченный существительными и глаголами, описан точно.
Бесконтекстные грамматики — это особая форма систем Полу-Туэ , которые в своей общей форме восходят к работам Акселя Туэ .
Формализм контекстно-свободных грамматик был разработан в середине 1950-х годов Ноамом Хомским , [3] а также их отнесение к особому типу формальных грамматик (которые он назвал грамматиками фразовой структуры ). [4] Некоторые авторы, однако, оставляют этот термин для более ограниченных грамматик в иерархии Хомского: контекстно-зависимые грамматики или контекстно-свободные грамматики. В более широком смысле грамматики фразовой структуры также известны как грамматики избирательного округа. Таким образом, определяющей чертой грамматик фразовой структуры является их приверженность отношению избирателя, в отличие от отношения зависимости, как в грамматиках зависимости . Хомского В рамках порождающей грамматики синтаксис естественного языка описывался контекстно-свободными правилами в сочетании с правилами преобразования. [5]
Блочная структура была введена в языки программирования в рамках проекта Алгол (1957–1960), который, как следствие, также включал контекстно-свободную грамматику для описания результирующего синтаксиса Алгола. Это стало стандартной особенностью компьютерных языков, а обозначение грамматик, используемых в конкретных описаниях компьютерных языков, стало известно как форма Бэкуса-Наура в честь двух членов комитета по разработке языка Алгол. [3] Аспект «блочной структуры», который фиксируют контекстно-свободные грамматики, настолько фундаментален для грамматики, что термины «синтаксис» и «грамматика» часто отождествляются с правилами контекстно-свободной грамматики, особенно в информатике. Формальные ограничения, не отраженные в грамматике, считаются частью «семантики» языка.
Контекстно-свободные грамматики достаточно просты, чтобы позволить создавать эффективные алгоритмы синтаксического анализа , которые для данной строки определяют, может ли она быть сгенерирована из грамматики и если да, то каким образом. Анализатор Эрли является примером такого алгоритма, в то время как широко используемые анализаторы LR и LL представляют собой более простые алгоритмы, которые работают только с более ограничительными подмножествами контекстно-свободных грамматик.
Формальные определения
[ редактировать ]Контекстно-свободная грамматика G определяется 4- кортежом , где [6]
- V — конечное множество; каждый элемент называется нетерминальным символом или переменной . Каждая переменная представляет отдельный тип фразы или предложения в предложении. Переменные также иногда называют синтаксическими категориями. Каждая переменная определяет подъязык языка, определенного G .
- Σ — конечное множество терминальных s, не пересекающихся с V , которые составляют фактическое содержание предложения. Набор терминалов представляет собой алфавит языка, определяемый G. грамматикой
- R — конечное отношение в , где звездочка обозначает операцию звезды Клини . Члены R называются правилами (перезаписи) или продукцией грамматики. (также обычно обозначается буквой P )
- S — начальная переменная (или начальный символ), используемая для представления всего предложения (или программы). Это должен быть элемент V .
Обозначение производственного правила
[ редактировать ]Производственное правило в R математически формализуется как пара , где является нетерминалом и представляет собой строку переменных и/или терминалов; вместо использования записи упорядоченной пары продукционные правила обычно записываются с использованием оператора стрелки с как его левая часть и β как его правая часть: .
Допускается, чтобы β была пустой строкой , и в этом случае ее принято обозначать ε. Форма называется ε -продукцией. [7]
Обычно все правые части одной и той же левой части перечисляются в одной строке, используя | ( вертикальная черта ), чтобы разделить их. Правила и следовательно, можно записать как . В этом случае, и называются соответственно первой и второй альтернативой.
Применение правил
[ редактировать ]Для любых строк , мы говорим, что u непосредственно дает v , записанный как , если с и такой, что и . Таким образом, v является результатом применения правила тебе .
Повторяющееся применение правил
[ редактировать ]Для любых строк мы говорим, u дает v или v получено что из u, если существует целое положительное число k и строки такой, что . Это отношение обозначается , или в некоторых учебниках. Если , отношение держит. Другими словами, и - это рефлексивное транзитивное замыкание (позволяющее строке поддаться самому себе) и транзитивное замыкание (требующее хотя бы одного шага) , соответственно.
Контекстно-свободный язык
[ редактировать ]Язык грамматики это набор
всех строк терминальных символов, полученных из начального символа.
Язык L называется контекстно-свободным языком (CFL), если существует CFG G такой, что .
Недетерминированные автоматы с выталкиванием распознают именно контекстно-свободные языки.
Примеры
[ редактировать ]Этот раздел нуждается в дополнительных цитатах для проверки . ( Июль 2018 г. ) |
Слова, объединенные в обратную сторону
[ редактировать ]Грамматика , с постановками
- С → аСа ,
- S → bSb ,
- S → ε ,
является контекстно-свободным. Это неправильно, поскольку включает ε-продукцию. Типичный вывод в этой грамматике:
- S → aSa → aaSaa → отецSbaa → отец
Это дает понять, что . Язык контекстно-свободный, однако можно доказать, что он не регулярен .
Если произведения
- С → а ,
- С → б ,
контекстно-свободная грамматика для множества всех палиндромов в алфавите { a , b } . добавляются, получается [8]
Правильно построенные скобки
[ редактировать ]Каноническим примером контекстно-свободной грамматики является сопоставление скобок, которое представляет общий случай. Имеются два терминальных символа «(» и «)» и один нетерминальный символ S. Правила производства таковы:
- С → СС ,
- С → ( S ) ,
- С → ()
Первое правило позволяет символу S умножаться; второе правило позволяет заключать символ S в соответствующие круглые скобки; и третье правило завершает рекурсию. [9]
Правильно сформированные вложенные скобки и квадратные скобки
[ редактировать ]Второй канонический пример — это два разных типа сопоставления вложенных круглых скобок, описываемых постановками:
- С → СС
- С → ()
- С → ( С )
- С → []
- С → [ С ]
с терминальными символами [ ] ( ) и нетерминальными S.
Из этой грамматики можно вывести следующую последовательность:
- ([ [ [ ()() [ ][ ] ] ]([ ]) ])
Соответствующие пары
[ редактировать ]В контекстно-свободной грамматике мы можем объединять символы в пары так же, как с помощью скобок . Самый простой пример:
- S → аСб
- С → аб
Эта грамматика порождает язык , что не является регулярным (согласно лемме о накачке для регулярных языков ).
Специальный символ ε обозначает пустую строку. Изменив приведенную выше грамматику на
- S → аСб
- С → е
мы получаем грамматику, порождающую язык вместо. Отличается только тем, что содержит пустую строку, а исходная грамматика ее не содержит.
Отдельное количество букв a и b
[ редактировать ]Контекстно-свободная грамматика языка, состоящая из всех строк над {a,b}, содержащих неравное количество букв a и b:
- С → Т | ты
- Т → НДС | ВаВ | ТаВ
- У → ВбУ | ВбВ | УбВ
- В → аВбВ | бВаВ | ε
Здесь нетерминал T может генерировать все строки с большим количеством a, чем b, нетерминал U генерирует все строки с большим количеством b, чем a, а нетерминал V генерирует все строки с равным количеством a и b. Исключение третьего варианта в правилах для T и U не ограничивает язык грамматики.
Второй блок букв двойного размера.
[ редактировать ]Другим примером нерегулярного языка является . Он является контекстно-свободным, поскольку его можно сгенерировать с помощью следующей контекстно-свободной грамматики:
- С → bSbb | А
- А → аА | ε
Логические формулы первого порядка
[ редактировать ]Правила формирования терминов и формул формальной логики соответствуют определению контекстно-свободной грамматики, за исключением того, что набор символов может быть бесконечным и может быть более одного начального символа.
Примеры языков, которые не являются контекстно-свободными
[ редактировать ]В отличие от правильно сформированных вложенных и квадратных скобок из предыдущего раздела, здесь не существует контекстно-свободной грамматики для генерации всех последовательностей двух разных типов круглых скобок, каждая из которых сбалансирована отдельно , независимо от другой , где эти два типа не должны вкладываться внутри одной. другое, например:
- [ ( ] )
или
- [ [ [ [(((( ] ] ] ]))))(([ ))(([ ))([ )( ])( ])( ])
Тот факт, что этот язык не является контекстно-свободным, можно доказать, используя лемму о накачке для контекстно-свободных языков и доказательство от противного, заметив, что все слова вида должно принадлежать языку. Вместо этого этот язык принадлежит к более общему классу и может быть описан конъюнктивной грамматикой , которая, в свою очередь, также включает в себя другие неконтекстно-свободные языки, такие как язык всех слов формы .
Регулярные грамматики
[ редактировать ]Каждая регулярная грамматика является контекстно-свободной, но не все контекстно-свободные грамматики являются регулярными. [10] Например, следующая контекстно-свободная грамматика также является регулярной.
- С → а
- С → аС
- С → бС
Терминалами здесь являются a и b единственным нетерминалом является S. , а Описанный язык представляет собой все непустые строки песок это заканчивается на .
Эта грамматика является регулярной : ни одно правило не имеет более одного нетерминала в правой части, и каждый из этих нетерминалов находится на одном и том же конце правой части.
Каждая регулярная грамматика напрямую соответствует недетерминированному конечному автомату , поэтому мы знаем, что это регулярный язык .
Используя вертикальные черты, приведенную выше грамматику можно описать более кратко следующим образом:
- С → а | АС | бакалавриат
Выводы и синтаксические деревья
[ редактировать ]Получение . строки для грамматики — это последовательность приложений грамматических правил, которые преобразуют начальный символ в строку Вывод доказывает, что строка принадлежит языку грамматики.
Вывод полностью определяется путем задания для каждого шага:
- правило, примененное на этом этапе
- появление его левой части, к которой оно применяется
Для ясности обычно также указывается промежуточная строка.
Например, с грамматикой:
- С → С + С
- С → 1
- С → а
строка
- 1 + 1 + а
может быть получен из начального символа S следующим выводом:
- С
- → S + S (по правилу 1. на S )
- → S + S + S (по правилу 1. на втором S )
- → 1 + S + S (по правилу 2. на первом S )
- → 1 + 1 + S (по правилу 2. на втором S )
- → 1 + 1 + a (по правилу 3. на третьем S )
Часто применяется стратегия, которая детерминированно выбирает следующий нетерминал для перезаписи:
- в крайнем левом выводе это всегда самый левый нетерминал;
- в крайнем правом выводе это всегда самый правый нетерминал.
При такой стратегии вывод полностью определяется последовательностью применяемых правил. Например, одно из крайних левых производных одной и той же строки — это
- С
- → S + S (по правилу 1 на крайнем левом S )
- → 1 + S (по правилу 2 на крайнем левом S )
- → 1 + S + S (по правилу 1 на крайнем левом S )
- → 1 + 1 + S (по правилу 2 на крайнем левом S )
- → 1 + 1 + a (по правилу 3 на крайнем левом S ),
который можно резюмировать как
- правило 1
- правило 2
- правило 1
- правило 2
- правило 3.
Один крайний правый вывод:
- С
- → S + S (по правилу 1 на крайнем правом S )
- → S + S + S (по правилу 1 на крайнем правом S )
- → S + S + a (по правилу 3 на крайнем правом S )
- → S + 1 + a (по правилу 2 на крайнем правом S )
- → 1 + 1 + a (по правилу 2 на крайнем правом S ),
который можно резюмировать как
- правило 1
- правило 1
- правило 3
- правило 2
- правило 2.
Различие между крайним левым выводом и крайним правым выводом важно, поскольку в большинстве парсеров преобразование входных данных определяется путем предоставления фрагмента кода для каждого грамматического правила, который выполняется всякий раз, когда правило применяется. Поэтому важно знать, определяет ли синтаксический анализатор крайний левый или крайний правый вывод, поскольку это определяет порядок, в котором будут выполняться фрагменты кода. См. пример парсеров LL и парсеров LR .
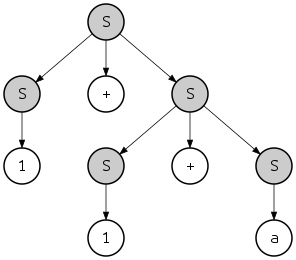
Вывод также в некотором смысле накладывает иерархическую структуру на производную строку. Например, если строка «1 + 1 + a» получена в соответствии с крайним левым выводом, описанным выше, структура строки будет такой:
- {{1} S + {{1} S + { a } S } S } S
где {...} S указывает на подстроку, признанную принадлежащей S . Эту иерархию также можно представить в виде дерева:
Это дерево называется деревом разбора или «конкретным синтаксическим деревом» строки, в отличие от абстрактного синтаксического дерева . В этом случае представленные крайний левый и крайний правый выводы определяют одно и то же дерево разбора; однако существует еще один крайний правый вывод той же строки
- С
- → S + S (по правилу 1 на крайнем правом S )
- → S + a (по правилу 3 на крайнем правом S )
- → S + S + a (по правилу 1 на крайнем правом S )
- → S + 1 + a (по правилу 2 на крайнем правом S )
- → 1 + 1 + a (по правилу 2 на крайнем правом S ),
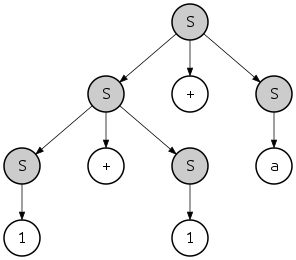
который определяет строку с другой структурой
- {{{1} S + {1} S } S + { a } S } S
и другое дерево разбора:
Однако обратите внимание, что оба дерева разбора могут быть получены как крайним левым, так и крайним правым выводом. Например, последнее дерево можно получить с помощью крайнего левого вывода следующим образом:
- С
- → S + S (по правилу 1 на крайнем левом S )
- → S + S + S (по правилу 1 на крайнем левом S )
- → 1 + S + S (по правилу 2 на крайнем левом S )
- → 1 + 1 + S (по правилу 2 на крайнем левом S )
- → 1 + 1 + a (по правилу 3 на крайнем левом S ),
Если строка в языке грамматики имеет более одного дерева синтаксического анализа, то грамматика называется неоднозначной грамматикой . Такие грамматики обычно трудно анализировать, поскольку анализатор не всегда может решить, какое грамматическое правило ему следует применить. Обычно неоднозначность является особенностью грамматики, а не языка, и можно найти однозначную грамматику, которая генерирует тот же контекстно-свободный язык. Однако есть определенные языки, которые могут быть созданы только с помощью неоднозначных грамматик; такие языки называются по своей сути неоднозначными языками .
Нормальные формы
[ редактировать ]Каждая контекстно-свободная грамматика без ε-продукции имеет эквивалентную грамматику в нормальной форме Хомского и грамматику в нормальной форме Грейбаха . «Эквивалент» здесь означает, что две грамматики порождают один и тот же язык.
Особенно простая форма правил продукции в грамматиках нормальной формы Хомского имеет как теоретическое, так и практическое значение. Например, учитывая контекстно-свободную грамматику, можно использовать нормальную форму Хомского для построения алгоритма с полиномиальным временем , который решает, находится ли данная строка на языке, представленном этой грамматикой, или нет ( алгоритм CYK ).
Свойства замыкания
[ редактировать ]Контекстно-свободные языки закрыты относительно различных операций, то есть если K и L языки контекстно-свободный, как и результат следующих операций:
- объединение К ∪ L ; конкатенация К ∘ L ; Клини Стар Л * [11]
- подстановка (в частности гомоморфизм ) [12]
- обратный гомоморфизм [13]
- пересечение с обычным языком [14]
Они не замкнуты ни относительно общего пересечения (следовательно, ни относительно дополнения ) и множества разностей. [15]
Решаемые проблемы
[ редактировать ]Ниже приведены некоторые разрешимые проблемы, связанные с контекстно-свободными грамматиками.
Разбор
[ редактировать ]Задача синтаксического анализа, проверка принадлежности данного слова языку, заданному контекстно-свободной грамматикой, разрешима с использованием одного из алгоритмов синтаксического анализа общего назначения:
- Алгоритм CYK (для грамматик в нормальной форме Хомского )
- Парсер Эрли
- GLR-парсер
- LL-парсер (только для соответствующего подкласса грамматик LL( k ))
бесконтекстный анализ грамматик нормальной формы Хомского показал, что Лесли Г. Валиант сводится к умножению булевых матриц , таким образом наследуя верхнюю границу сложности O ( n 2.3728639 ). [16] [17] [примечание 1] И наоборот, Лилиан Ли показала O ( n 3-е ) Умножение булевой матрицы должно быть сведено к O ( n 3−3е ) Разбор CFG, устанавливая тем самым некую нижнюю границу для последнего. [18]
Достижимость, продуктивность, обнуляемость
[ редактировать ]| Пример грамматики: | |||
|---|---|---|---|
| С → Бб | Копия | Ээ | |||
| Б → Бб | б | |||
| С → С | |||
| Д → Бд | компакт- диск | д | |||
| Е → Ээ | |||
Нетерминальный символ называется продуктивным , или производящим , если имеется вывод для какой-то строки терминальных символов. называется достижимым, если существует вывод для некоторых строк нетерминальных и терминальных символов от начального символа. называется бесполезным , если оно недостижимо или непродуктивно. называется обнуляемым, если существует вывод . Правило называется ε-продукцией . Вывод называется циклом .
Известно, что алгоритмы исключают из заданной грамматики, не меняя ее сгенерированный язык,
- непродуктивные символы, [19] [примечание 2]
- недостижимые символы, [21] [22]
- ε-продукции, за одним возможным исключением, [примечание 3] [23] и
- циклы. [примечание 4]
В частности, альтернативу, содержащую бесполезный нетерминальный символ, можно удалить из правой части правила.Такие правила и альтернативы называются бесполезными . [24]
В изображенном примере грамматики нетерминал D недоступен, а E непродуктивен, а C → C вызывает цикл.Следовательно, пропуск последних трех правил не меняет язык, порожденный грамматикой, равно как и пропуск альтернатив «| Cc | Ee » в правой части правила для S .
Контекстно-свободная грамматика называется правильной, если она не имеет ни бесполезных символов, ни ε-продукций, ни циклов. [25] Комбинируя приведенные выше алгоритмы, любую контекстно-свободную грамматику, не порождающую ε, можно преобразовать в слабо эквивалентную собственную.
регулярности и LL( k ) Проверка
[ редактировать ]Можно решить, ли данная грамматика является регулярной грамматикой . [26] а также является ли это LL( k ) грамматикой для данного k ≥0. [27] : 233 Если k не задано, последняя проблема неразрешима. [27] : 252
Учитывая контекстно-свободную грамматику, невозможно решить, является ли ее язык регулярным. [28] и не является ли это языком LL( k ) для данного k . [27] : 254
Пустота и конечность
[ редактировать ]Существуют алгоритмы, позволяющие решить, является ли язык данной контекстно-свободной грамматики пустым, а также конечным ли он. [29]
Неразрешимые проблемы
[ редактировать ]Некоторые вопросы, неразрешимые для более широких классов грамматик, становятся разрешимыми для контекстно-свободных грамматик; например, проблема пустоты (генерирует ли грамматика вообще какие-либо терминальные строки) неразрешима для контекстно-зависимых грамматик , но разрешима для контекстно-свободных грамматик.
Однако многие проблемы неразрешимы даже для контекстно-свободных грамматик; наиболее известные из них рассматриваются ниже.
Универсальность
[ редактировать ]Учитывая CFG, генерирует ли он язык всех строк в алфавите терминальных символов, используемых в его правилах? [30] [31]
Сведение к этой проблеме можно продемонстрировать на основе хорошо известной неразрешимой проблемы определения того, принимает ли машина Тьюринга конкретный ввод ( проблема остановки ). В сокращении используется концепция истории вычислений , строки, описывающей все вычисления машины Тьюринга . Можно построить CFG, который генерирует все строки, которые не принимают истории вычислений для конкретной машины Тьюринга на определенном входе, и, таким образом, он будет принимать все строки только в том случае, если машина не принимает этот вход.
Языковое равенство
[ редактировать ]Учитывая два CFG, генерируют ли они один и тот же язык? [31] [32]
Неразрешимость этой проблемы является прямым следствием предыдущей: невозможно даже решить, эквивалентна ли CFG тривиальной CFG, определяющей язык всех строк.
Языковое включение
[ редактировать ]Учитывая два CFG, может ли первый сгенерировать все строки, которые может сгенерировать второй? [31] [32]
Если бы эта проблема была разрешима, то можно было бы решить и равенство языков: две CFG и сгенерировать тот же язык, если является подмножеством и является подмножеством .
Нахождение на более низком или более высоком уровне иерархии Хомского
[ редактировать ]Используя теорему Грейбаха , можно показать, что две следующие проблемы неразрешимы:
- Учитывая контекстно-зависимую грамматику , описывает ли она контекстно-свободный язык?
- Учитывая контекстно-свободную грамматику, описывает ли она обычный язык ? [31] [32]
Грамматическая неоднозначность
[ редактировать ]Учитывая CFG, является ли это двусмысленным ?
Неразрешимость этой проблемы следует из того, что если бы существовал алгоритм определения неоднозначности, то можно было бы решить проблему соответствия Поста , которая, как известно, неразрешима. [33] Это можно доказать с помощью леммы Огдена . [34]
Языковая разобщенность
[ редактировать ]Учитывая две CFG, существует ли какая-либо строка, выводимая из обеих грамматик?
Если бы эта проблема была разрешима, то можно было бы решить и неразрешимую проблему почтового соответствия (PCP): заданные строки над каким-то алфавитом , пусть грамматика состоят из правила
- ;
где обозначает перевернутую строку и не встречается среди ; и пусть грамматика состоят из правила
- ;
Тогда экземпляр PCP, заданный имеет решение тогда и только тогда, когда и поделиться производной строкой. Слева от строки (перед ) будет представлять верхнюю часть решения для экземпляра PCP, а правая сторона будет нижней, наоборот.
Расширения
[ редактировать ]Очевидный способ расширить формализм контекстно-свободной грамматики — позволить нетерминалам иметь аргументы, значения которых передаются внутри правил. такие функции естественного языка, как соглашение и ссылка Это позволяет естественным образом выражать , а также аналоги языка программирования, такие как правильное использование и определение идентификаторов. Например, теперь мы можем легко выразить, что в английских предложениях подлежащее и глагол должны совпадать по числу. В информатике примеры такого подхода включают аффиксные грамматики , атрибутивные грамматики , индексированные грамматики и двухуровневые грамматики Ван Вейнгаардена . Подобные расширения существуют и в лингвистике.
Расширенная бесконтекстная грамматика (или обычная грамматика правой части ) — это такая грамматика, в которой правая часть правил продукции может быть регулярным выражением над терминалами и нетерминалами грамматики. Расширенные контекстно-свободные грамматики описывают именно контекстно-свободные языки. [35]
Другое расширение — разрешить появление дополнительных символов терминала в левой части правил, ограничивая их применение. Это порождает формализм контекстно-зависимых грамматик .
Подклассы
[ редактировать ]Существует ряд важных подклассов контекстно-свободных грамматик:
- LR( k ) Грамматики (также известные как детерминированные контекстно-свободные грамматики ) позволяют выполнять синтаксический анализ (распознавание строк) с помощью детерминированных автоматов с выталкиванием (PDA), но они могут описывать только детерминированные контекстно-свободные языки .
- Простые LR грамматики Look-Ahead LR — это подклассы, которые позволяют еще больше упростить синтаксический анализ. SLR и LALR распознаются с помощью того же КПК, что и LR, но в большинстве случаев с помощью более простых таблиц.
- Грамматики LL( k ) и LL( * ) позволяют анализировать путем прямого построения крайнего левого вывода, как описано выше, и описывают еще меньше языков.
- Простые грамматики - это подкласс грамматик LL (1), который в основном интересен своим теоретическим свойством, заключающимся в том, что языковое равенство простых грамматик разрешимо, а включение языков - нет.
- Грамматики в квадратных скобках обладают тем свойством, что терминальные символы делятся на пары левых и правых скобок, которые всегда совпадают в правилах.
- В линейных грамматиках нет правил с более чем одним нетерминалом в правой части.
- Регулярные грамматики являются подклассом линейных грамматик и описывают регулярные языки, т. е. соответствуют конечным автоматам и регулярным выражениям .
Анализ LR расширяет анализ LL для поддержки более широкого диапазона грамматик; в свою очередь, обобщенный анализ LR расширяет анализ LR для поддержки произвольных контекстно-свободных грамматик. На LL-грамматиках и LR-грамматиках он по существу выполняет синтаксический анализ LL и LR-анализ соответственно, тогда как на недетерминированных грамматиках он настолько эффективен, насколько можно ожидать. Хотя синтаксический анализ GLR был разработан в 1980-х годах, многие новые определения языка и генераторы синтаксических анализаторов продолжают основываться на синтаксическом анализе LL, LALR или LR и по сей день.
Лингвистические приложения
[ редактировать ]Хомский изначально надеялся преодолеть ограничения контекстно-свободных грамматик, добавив правила преобразования . [4]
Такие правила являются еще одним стандартным приемом традиционной лингвистики; например пассивизация на английском языке. Большая часть порождающей грамматики была посвящена поиску способов совершенствования описательных механизмов грамматики фразовой структуры и правил преобразования, позволяющих выражать именно те вещи, которые действительно позволяет естественный язык. Разрешение произвольных преобразований не достигает этой цели: они слишком эффективны и являются полными по Тьюрингу , если не добавлены существенные ограничения (например, никаких преобразований, которые вводят, а затем переписывают символы в бесконтекстной манере).
Общая позиция Хомского относительно неконтекстной свободы естественного языка с тех пор сохраняется: [36] хотя его конкретные примеры о неадекватности контекстно-свободных грамматик с точки зрения их слабой порождающей способности были позже опровергнуты. [37] Джеральд Газдар и Джеффри Пуллум утверждали, что, несмотря на несколько неконтекстно-свободных конструкций на естественном языке (таких как перекрестные зависимости в швейцарском немецком языке), [36] и дублирование в Бамбаре [38] ), подавляющее большинство форм естественного языка действительно являются контекстно-свободными. [37]
См. также
[ редактировать ]- Разбор грамматики выражений
- Стохастическая контекстно-свободная грамматика
- Алгоритмы генерации контекстно-свободной грамматики
- Лемма о накачке для контекстно-свободных языков
Ссылки
[ редактировать ]- ^ Брайан В. Керниган и Деннис М. Ричи (апрель 1988 г.). Язык программирования Си . Серия программного обеспечения Prentice Hall (2-е изд.). Энглвуд Клиффс / Нью-Джерси: Прентис Холл. ISBN 0131103628 . Здесь: Приложение.А
- ^ Введение в теорию автоматов, языки и вычисления , Джон Э. Хопкрофт, Раджив Мотвани, Джеффри Д. Уллман, Аддисон Уэсли, 2001, стр.191
- ^ Jump up to: а б Хопкрофт и Ульман (1979) , с. 106.
- ^ Jump up to: а б Хомский, Ноам (сентябрь 1956 г.), «Три модели описания языка», IEEE Transactions on Information Theory , 2 (3): 113–124, doi : 10.1109/TIT.1956.1056813 , S2CID 19519474
- ^ Юрафский, Дэниел; Мартин, Джеймс Х. (29 декабря 2021 г.). «Грамматика округа» (PDF) . Стэнфордский университет . Архивировано (PDF) из оригинала 14 марта 2017 г. Проверено 28 октября 2022 г.
- ^ Обозначения здесь взяты из Sipser (1997) , стр. 94. Hopcroft & Ullman (1979) (стр. 79) определяют контекстно-свободные грамматики как четырехкортежи таким же образом, но с другими именами переменных.
- ^ Хопкрофт и Уллман (1979) , стр. 90–92.
- ^ Хопкрофт и Ульман (1979) , упражнение 4.1a, стр. 103.
- ^ Хопкрофт и Ульман (1979) , Упражнение 4.1b, стр. 103.
- ^ Ахо, Альфред Вайно ; Лам, Моника С .; Сетхи, Рави ; Уллман, Джеффри Дэвид (2007). «4.2.7 Контекстно-свободные грамматики и регулярные выражения» (печать) . Составители: принципы, методы и инструменты (2-е изд.). Бостон, Массачусетс, США: Пирсон Аддисон-Уэсли. стр. 205–206 . ISBN 9780321486813 .
Любая конструкция, которая может быть описана регулярным выражением, может быть описана [бесконтекстной] грамматикой, но не наоборот.
- ^ Хопкрофт и Ульман (1979), стр.131, Теорема 6.1.
- ^ Хопкрофт и Ульман (1979), стр. 131–132, Теорема 6.2.
- ^ Хопкрофт и Уллман (1979), стр. 132–134, Теорема 6.3.
- ^ Хопкрофт и Ульман (1979), стр. 135–136, Теорема 6.5.
- ^ Хопкрофт и Ульман (1979), стр. 134–135, Теорема 6.4.
- ^ Лесли Валиант (январь 1974 г.). Общее бесконтекстное распознавание менее чем за кубическое время (Технический отчет). Университет Карнеги-Меллон. п. 11.
- ^ Лесли Г. Валиант (1975). «Общее контекстно-свободное распознавание менее чем за кубическое время» . Журнал компьютерных и системных наук . 10 (2): 308–315. дои : 10.1016/s0022-0000(75)80046-8 .
- ^ Лилиан Ли (2002). «Быстрый контекстно-свободный анализ грамматики требует быстрого умножения логических матриц» (PDF) . Дж АСМ . 49 (1): 1–15. arXiv : cs/0112018 . дои : 10.1145/505241.505242 . S2CID 1243491 . Архивировано (PDF) из оригинала 27 апреля 2003 г.
- ^ Хопкрофт и Ульман (1979) , Лемма 4.1, с. 88.
- ^ Эйкен, А.; Мерфи, Б. (1991). «Реализация регулярных древовидных выражений». Конференция ACM по функциональным языкам программирования и архитектуре компьютеров . стр. 427–447. CiteSeerX 10.1.1.39.3766 . ; здесь: Раздел 4
- ^ Хопкрофт и Ульман (1979) , Лемма 4.2, с. 89.
- ^ Хопкрофт, Мотвани и Ульман (2003) , Теорема 7.2, раздел 7.1, стр.255 и далее.
- ^ Хопкрофт и Ульман (1979) , Теорема 4.3, с. 90.
- ^ Джон Э. Хопкрофт; Раджив Мотвани; Джеффри Д. Уллман (2003). Введение в теорию автоматов, языки и вычисления . Эддисон Уэсли. ; здесь: п.7.1.1, стр.256
- ^ Нийхолт, Антон (1980), Контекстно-свободные грамматики: оболочки, нормальные формы и синтаксический анализ , Конспекты лекций по информатике, том. 93, Спрингер, с. 8, ISBN 978-3-540-10245-8 , МР 0590047 .
- ^ Это легко увидеть из определений грамматики.
- ^ Jump up to: а б с DJ Розенкранц и Р.Э. Стернс (1970). «Свойства детерминированных нисходящих грамматик» . Информация и контроль . 17 (3): 226–256. дои : 10.1016/S0019-9958(70)90446-8 .
- ^ Хопкрофт и Уллман (1979) , Упражнение 8.10a, стр. 214. Проблема остается неразрешимой, даже если язык создан с помощью «линейной» контекстно-свободной грамматики (т. е. с не более чем одним нетерминалом в правой части каждого правила, ср. упражнение 4.20, стр. 105).
- ^ Хопкрофт и Ульман (1979), стр. 137–138, Теорема 6.6.
- ^ Сипсер (1997) , Теорема 5.10, с. 181.
- ^ Jump up to: а б с д Хопкрофт и Ульман (1979) , с. 281.
- ^ Jump up to: а б с Хазевинкель, Михель (1994), Математическая энциклопедия: обновленный и аннотированный перевод советской «Математической энциклопедии» , Springer, Vol. IV, с. 56, ISBN 978-1-55608-003-6 .
- ^ Хопкрофт и Ульман (1979 , стр. 200–201, теорема 8.9)
- ^ Огден, Уильям (сентябрь 1968 г.). «Полезный результат для доказательства внутренней двусмысленности» . Теория математических систем . 2 (3): 191–194. дои : 10.1007/bf01694004 . ISSN 0025-5661 . S2CID 13197551 . Здесь: стр.4
- ^ Норвелл, Теодор. «Краткое введение в регулярные выражения и контекстно-свободные грамматики» (PDF) . п. 4. Архивировано (PDF) из оригинала 24 марта 2005 г. Проверено 24 августа 2012 г.
- ^ Jump up to: а б Шибер, Стюарт (1985), «Свидетельства против контекстной свободы естественного языка» (PDF) , Linguistics and Philosophy , 8 (3): 333–343, doi : 10.1007/BF00630917 , S2CID 222277837 , заархивировано (PDF) из оригинал от 15 апреля 2004 г.
- ^ Jump up to: а б Пуллум, Джеффри К.; Джеральд Газдар (1982), «Естественные языки и контекстно-свободные языки», Linguistics and Philosophy , 4 (4): 471–504, doi : 10.1007/BF00360802 , S2CID 189881482 .
- ^ Кали, Кристофер (1985), «Сложность словарного запаса Бамбары», Linguistics and Philosophy , 8 (3): 345–351, doi : 10.1007/BF00630918 , S2CID 189881984 .
Примечания
[ редактировать ]- ^ В статьях Валианта O ( n 2.81 ) дана самая известная на тот момент верхняя граница. См. раздел «Умножение матриц № Вычислительная сложность», чтобы узнать о связанных улучшениях с тех пор.
- ^ Для обычных древовидных грамматик Эйкен и Мерфи предлагают алгоритм с фиксированной точкой для обнаружения непродуктивных нетерминалов. [20]
- ^ Если грамматика может генерировать , правило нельзя избежать.
- ^ Это следствие теоремы об устранении единичного производства в Hopcroft & Ullman (1979), стр.91, теорема 4.4.
Дальнейшее чтение
[ редактировать ]- Хопкрофт, Джон Э .; Уллман, Джеффри Д. (1979), Введение в теорию автоматов, языки и вычисления , Аддисон-Уэсли . Глава 4: Контекстно-свободные грамматики, стр. 77–106; Глава 6: Свойства контекстно-свободных языков, стр. 125–137.
- Хопкрофт; Мотвани, Раджив; Уллман, Джеффри Д. (2003). Введение в теорию автоматов, языки и вычисления (2-е изд.). Река Аппер-Седл: Pearson Education International. ISBN 978-0321210296 .
- Сипсер, Майкл (1997), Введение в теорию вычислений , PWS Publishing, ISBN 978-0-534-94728-6 . Глава 2: Контекстно-свободные грамматики, стр. 91–122; Раздел 4.1.2: Решаемые проблемы, касающиеся контекстно-свободных языков, стр. 156–159; Раздел 5.1.1: Сокращение с помощью истории вычислений: стр. 176–183.
- Дж. Берстель, Л. Боассон (1990). Ян ван Леувен (ред.). Контекстно-свободные языки . Справочник по теоретической информатике. Том. Б. Эльзевир. стр. 59–102.
Внешние ссылки
[ редактировать ]- Программисты могут найти ответ на обмен стеком полезным.
- Разработчик CFG, созданный Кристофером Вонгом из Стэнфордского университета в 2014 году; изменен Кевином Гиббонсом в 2015 году.














































![{\displaystyle {(}^{n}{[}^{n}{)}^{n}{]}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/970271f0d3f69633f9882b0249b003ac8fb4344e)