Задача 100 заключенных

Каждый заключенный должен найти свой номер в одном из 100 ящиков, но может открыть только 50 ящиков.

Задача о 100 заключенных — математическая задача теории вероятностей и комбинаторики . В этой задаче 100 пронумерованных заключенных должны найти свои номера в одном из 100 ящиков, чтобы выжить. Правила гласят, что каждый заключенный может открывать только 50 ящиков и не может общаться с другими заключенными. На первый взгляд ситуация кажется безнадежной, но продуманная стратегия дает заключенным реальный шанс на выживание.

Анна Галь и Питер Бро Мильтерсен впервые предложили эту проблему в 2003 году.

Проблема

Проблема 100 заключенных имеет в литературе разные интерпретации. Следующая версия принадлежит Филиппу Флажоле и Роберту Седжвику :

Директор тюрьмы предлагает 100 заключенным, приговоренным к смертной казни, пронумерованным от 1 до 100, последний шанс. В комнате есть шкаф со 100 ящиками. В каждый закрытый ящик директор случайным образом кладет по одному номеру заключенного. Заключенные входят в комнату один за другим. Каждый заключенный может открыть и просмотреть 50 ящиков в любом порядке. После этого ящики снова закрываются. Если в ходе обыска каждый заключенный найдет свой номер в одном из ящиков, все заключенные будут помилованы. Если хотя бы один заключенный не найдет свой номер, все заключенные погибнут. Прежде чем первый заключенный войдет в комнату, заключенные могут обсудить стратегию, но не могут общаться, когда первый заключенный входит, чтобы заглянуть в ящики. Какова лучшая стратегия заключенных?

выберет 50 ящиков Если каждый заключенный самостоятельно и случайным образом , вероятность того, что один заключенный найдет их число, составит 50%. Вероятность того, что все заключенные найдут свои номера, является произведением одиночных вероятностей, то есть ( ⁠ 1 / 2 ⁠ ) ¹⁰⁰ ≈ 0,000 000 000 000 000 000 000 000 000 0008 , исчезающе малое число. Ситуация кажется безнадежной.

Решение

Стратегия

Удивительно, но существует стратегия, обеспечивающая вероятность выживания более 30%. Залог успеха в том, что заключенным не нужно заранее решать, какие ящики открывать. Каждый заключенный может использовать информацию, полученную из содержимого каждого ящика, который он уже открыл, чтобы решить, какой из них открыть следующим. Еще одно важное наблюдение состоит в том, что таким образом успех одного заключенного не зависит от успеха других заключенных, поскольку все они зависят от того, как распределены числа.

Для описания стратегии не только заключенные, но и ящики пронумерованы от 1 до 100; например, ряд за рядом, начиная с верхнего левого ящика. Стратегия теперь следующая:

1. Каждый заключенный сначала открывает ящик, помеченный своим номером.
2. Если в этом ящике содержится их номер, значит, они готовы и прошли успешно.
3. В противном случае в ящике содержится номер другого заключенного, и затем они открывают ящик, отмеченный этим номером.
4. Заключенный повторяет шаги 2 и 3 до тех пор, пока не найдет свой номер, или не потерпит неудачу, потому что номер не найден в первых пятидесяти открытых ящиках.

Если бы заключенный мог продолжать таким образом бесконечно, он неизбежно вернулся бы к тому ящику, с которого начал, образуя цикл перестановок (см. Ниже ). Начав со своего номера, заключенный гарантирует, что он находится в определенном цикле ящиков, содержащем его номер. Единственный вопрос заключается в том, длиннее ли какой-либо цикл более пятидесяти ящиков - и только один цикл может быть слишком длинным, поскольку максимум один может составлять более половины от общего числа ящиков.

Примеры

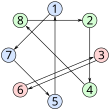
Причина, по которой эта стратегия является многообещающей, иллюстрируется следующим примером с использованием 8 заключенных и ящиков, где каждый заключенный может открыть 4 ящика. Начальник тюрьмы разложил номера заключенных по ящикам следующим образом:

количество ящиков	1	2	3	4	5	6	7	8
количество заключенных	7	4	6	8	1	3	5	2

Теперь заключенные действуют следующим образом:

• Заключенный 1 сначала открывает ящик 1 и находит номер 7. Затем он открывает ящик 7 и находит номер 5. Затем он открывает ящик 5, где находит свой номер и добивается успеха.
• Заключенный 2 открывает ящики 2, 4 и 8 в этом порядке. В последнем ящике они находят свой номер — 2.
• Заключенный 3 открывает ящики 3 и 6, где находит свой номер.
• Заключенный 4 открывает ящики 4, 8 и 2, где находит свой номер. Это тот же цикл, с которым столкнулся заключенный 2 и с которым столкнется заключенный 8. Каждый из этих заключенных найдет свой номер в третьем открытом ящике.
• Заключенные с 5 по 7 также найдут свои номера аналогичным образом.

В этом случае все заключенные узнают свои номера. Однако это не всегда так. Например, небольшое изменение количества перепутанных ящиков 5 и 8 приведет к тому, что заключенный 1 потерпит неудачу после открытия 1, 7, 5 и 2 (и не нахождения своего собственного номера):

количество ящиков	1	2	3	4	5	6	7	8
количество заключенных	7	4	6	8	2	3	5	1

А в следующей схеме заключенный 1 открывает ящики 1, 3, 7 и 4, и в этот момент им приходится безуспешно останавливаться:

количество ящиков	1	2	3	4	5	6	7	8
количество заключенных	3	1	7	5	8	6	4	2

Действительно, все заключенные, за исключением шестерых (которые добиваются прямого успеха), терпят неудачу.

Представление перестановок

Графические представления перестановок (1 7 5)(2 4 8)(3 6) и (1 3 7 4 5 8 2)(6)

Распределение директором тюрьмы номеров заключенных по ящикам математически можно описать как перестановку чисел от 1 до 100. Такая перестановка представляет собой взаимно однозначное отображение набора натуральных чисел от 1 до 100 в себя. Последовательность чисел, которая после многократного применения перестановки возвращается к первому числу, называется циклом перестановки. Любую перестановку можно разложить на непересекающиеся циклы, то есть циклы, не имеющие общих элементов. Перестановку первого примера выше можно записать в обозначениях цикла как

$(1~7~5)(2~4~8)(3~6)$

и, таким образом, состоит из двух циклов длины 3 и одного цикла длины 2. Перестановка третьего примера соответственно имеет вид

$(1~3~7~4~5~8~2)(6)$

и состоит из цикла длины 7 и цикла длины 1. Обозначение цикла не уникально, поскольку цикл длины $l$ можно написать в $l$ разными способами в зависимости от стартового номера цикла. При открытии ящиков с использованием описанной выше стратегии каждый заключенный выполняет один цикл, который всегда заканчивается его собственным номером. В случае восьми заключенных эта стратегия следования за циклом успешна тогда и только тогда, когда длина самого длинного цикла перестановки не превышает 4. Если перестановка содержит цикл длиной 5 или более, все заключенные, номера которых лежат в такой цикл не достигает своего числа после четырех шагов.

Вероятность успеха

Распределение вероятностей длины самого длинного цикла случайной перестановки чисел от 1 до 100. Зеленая область соответствует вероятности выживания заключенных.

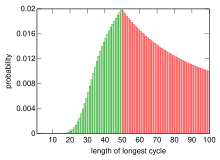
В исходной задаче 100 заключенных добьются успеха, если длина самого длинного цикла перестановки не превышает 50. Таким образом, вероятность их выживания равна вероятности того, что случайная перестановка чисел от 1 до 100 не содержит циклов длины большей чем 50. Эта вероятность определяется следующим.

Перестановка чисел от 1 до 100 может содержать не более одного цикла длиной $l>50$. Есть точно ${\tbinom {100}{l}}$ способы выбора чисел такого цикла (см. сочетание ). Внутри этого цикла эти числа можно расположить в $(l-1)!$ способы, поскольку существуют $l$ перестановки для представления различных циклов длины $l$ из-за циклической симметрии. Остальные числа можно расположить в $(100-l)!$ пути. Следовательно, количество перестановок чисел от 1 до 100 с циклом длины $l>50$ равно

${\binom {100}{l}}\cdot (l-1)!\cdot (100-l)!={\frac {100!}{l}}.$

Вероятность того, что ( равномерно распределенная ) случайная перестановка не содержит циклов длиной более 50, рассчитывается по формуле для одиночных событий и формуле для дополнительных событий, определяемой следующим образом:

$1-{\frac {1}{100!}}\left({\frac {100!}{51}}+\ldots +{\frac {100!}{100}}\right)=1-\left({\frac {1}{51}}+\ldots +{\frac {1}{100}}\right)=1-(H_{100}-H_{50})\approx 0.31183,$

где $H_{n}$ это $n$-й номер гармоники . Таким образом, при использовании стратегии следования циклу заключенные выживают в удивительных 31% случаев.

Асимптотика

Номера гармоник приблизительно определяются площадью под гиперболой и поэтому могут быть аппроксимированы логарифмом.

Если $2n$ вместо 100 заключенных считаются, где $n$ произвольное натуральное число, вероятность выживания заключенных при использовании стратегии следования циклу определяется выражением

$1-(H_{2n}-H_{n})=1-(H_{2n}-\ln 2n)+(H_{n}-\ln n)-\ln 2.$

С постоянной Эйлера-Машерони $\gamma$, для $n\to \infty$

$\lim _{n\to \infty }(H_{n}-\ln n)=\gamma$

имеет место, что приводит к асимптотической вероятности выживания

$\lim _{n\to \infty }(1-H_{2n}+H_{n})=1-\gamma +\gamma -\ln 2=1-\ln 2\approx 0.30685.$

Поскольку последовательность вероятностей монотонно убывает , заключенные выживают при использовании стратегии следования циклу более чем в 30% случаев независимо от количества заключенных.

Оптимальность

В 2006 году Юджин Кертин и Макс Варшауэр доказали оптимальность стратегии следования за циклом. Доказательство основано на эквиваленте аналогичной задачи, в которой всем заключенным разрешено присутствовать в комнате и наблюдать за открытием ящиков. Математически эта эквивалентность основана на лемме о переходе Фоаты , взаимно однозначном соответствии (канонического) обозначения цикла и однострочного обозначения перестановок. Во второй задаче вероятность выживания не зависит от выбранной стратегии и равна вероятности выживания в исходной задаче со стратегией следования по циклу. Поскольку произвольная стратегия для исходной задачи также может быть применена ко второй задаче, но не может обеспечить там более высокую вероятность выживания, стратегия следования по циклу должна быть оптимальной.

История

Проблема 100 заключенных была впервые рассмотрена в 2003 году Анной Галь и Питером Бро Мильтерсеном в материалах 30- го Международного коллоквиума по автоматам, языкам и программированию ( ICALP ). В их версии игрок А (начальник тюрьмы) случайным образом раскрашивает полоски бумаги с именами игроков команды Б (заключенных) в красный или синий цвет и кладет каждую полоску в отдельную коробку. Некоторые поля могут быть пустыми (см. ниже ). Для победы своей команды каждый игрок команды Б должен правильно угадать свой цвет после открытия половины коробок. Первоначально Галь и Мильтерсен предположили, что вероятность выигрыша быстро стремится к нулю с увеличением числа игроков. Однако Свен Скюм, коллега из Орхусского университета , обратил внимание на стратегию следования циклу для случая этой задачи, когда пустых ящиков нет. Поиск этой стратегии был оставлен открытым в качестве упражнения в публикации. Статья была удостоена награды за лучшую работу.

Весной 2004 года задача появилась в Джо Бюлера и Элвина Берлекэмпа колонке-головоломке в ежеквартальном журнале The Emissary of the Mathematical Sciences Research Institute . Таким образом, авторы заменили коробки на ПЗУ , а цветные полоски бумаги — на подписанные номера. Авторы отметили, что вероятность выигрыша может быть увеличена и в том случае, если участники команды не найдут свои номера. Если данный ответ является произведением всех найденных знаков и если длина самого длинного цикла равна половине (четного) числа игроков плюс один, то все члены команды в этом цикле либо все угадывают неправильно, либо все угадывают правильно. Даже если такое расширение стратегии предлагает видимое улучшение для небольшого числа игроков, оно становится незначительным, когда число игроков становится большим.

В последующие годы задача вошла в математическую литературу, где ее формулировали по-разному, например, с картами на столе. или кошельки в шкафчиках ( загадка шкафчика ). В форме задачи пленника она была поставлена ​​в 2006 году Кристофом Пёппе в журнале Spektrum der Wissenschaft и Питером Винклером в College Mathematics Journal . С небольшими изменениями эту форму переняли Филипп Флажоле, Роберт Седжвик и Ричард П. Стэнли в своих учебниках по комбинаторике. Задача, или загадка, вместе с подробным объяснением решения была представлена ​​каналом Veritasium в видеоролике на YouTube в 2023 году .

Варианты

Пустые коробки

Сначала Галь и Мильтерсен рассмотрели в своей статье случай, когда количество ящиков в два раза превышает количество членов команды, а половина ящиков пуста. Это более сложная проблема, поскольку пустые ячейки никуда не ведут и, следовательно, стратегия следования за циклом не может быть применена. Вопрос о том, стремится ли в этом случае вероятность победы к нулю с ростом числа членов команды, остается открытым.

В 2005 году Навин Гоял и Майкл Сакс разработали стратегию для команды B, основанную на стратегии следования циклу для более общей задачи, в которой доля пустых коробок, а также доля коробок, которые может открыть каждый член команды, являются переменными. Вероятность выигрыша в этом случае все еще стремится к нулю, но медленнее, чем предполагали Гал и Мильтерсен. Если количество членов команды и доля открываемых коробок фиксированы, вероятность победы остается строго больше нуля при добавлении большего количества пустых коробок.

Дэвид Эвис и Энн Бродбент рассмотрели в 2009 году квантово-теоретический вариант, в котором команда Б уверенно побеждает.

Злонамеренный директор

В случае, если директору тюрьмы не нужно распределять номера по ящикам случайным образом, и он понимает, что заключенные могут применять вышеупомянутую стратегию, и угадывает нумерацию ячеек, которые заключенные будут применять (например, номера, указанные на ящиках), он может сорвать стратегию. Для этого им достаточно добиться того, чтобы их распределение номеров заключенных по ящикам представляло собой перестановку с циклом длиной больше 50. Заключенные, в свою очередь, могут противодействовать этому, договариваясь между собой о конкретной случайной нумерации ящиков, при условии, что директор этого не подслушает или не потрудится отреагировать заменой цифр в ящиках до того, как впустят заключенных.

Один заключенный может внести одно изменение

В случае, если один заключенный сможет первым войти в комнату, осмотреть все ящики , а затем поменять содержимое двух ящиков, все заключенные выживут. Это так, поскольку любой цикл длиной больше 50 можно прервать, так что можно гарантировать, что все циклы имеют длину не более 50.

Для достаточно большого количества заключенных $N$, они могут обеспечить свой побег, открыв значительно меньше половины ящиков. В частности, каждому заключенному необходимо открыть только $O\left(N{\frac {\log \log N}{\log N}}\right)$ ящики для обеспечения побега всех заключенных.

Любой заключенный, нашедший свой номер, освобождается.

В варианте, когда любой заключенный, нашедший свой номер, оказывается на свободе, ожидаемая вероятность выживания человека при случайной перестановке выглядит следующим образом:

Без стратегии: ${\frac {1}{2}}$

Со стратегией исходной проблемы: $(1-\ln(2))\cdot 1+\sum _{k=\lfloor n/2\rfloor +1}^{N}{\frac {1}{k}}\left(1-{\frac {k}{n}}\right)=1-\ln(2)+\sum _{\lfloor n/2\rfloor +1}^{N}{\frac {1}{k}}-\sum _{k=\lfloor n/2\rfloor +1}^{N}{\frac {1}{n}}=1-\ln(2)+\ln(2)-{\frac {1}{2}}={\frac {1}{2}}$

Примечательно, что хотя мы получаем одинаковые ожидаемые значения, они происходят из очень разных распределений. При использовании второй стратегии некоторым заключенным просто суждено умереть или выжить при определенной расстановке сил, а при использовании первой стратегии (т. е. отсутствия стратегии) ​​существует «действительно» шанс 1/2 для каждой перестановки.

Проблема Монти Холла

В 2009 году Адам С. Ландсберг предложил следующий более простой вариант задачи о 100 заключенных, основанный на известной задаче Монти Холла :

За тремя закрытыми дверями случайным образом распределены машина, ключи от машины и коза. Играют два игрока: первый должен найти машину, второй — ключи от машины. Только если оба игрока добьются успеха, они смогут поехать на машине домой. Первый игрок входит в комнату и может последовательно открыть две двери из трех. Если они успешны, двери снова закрываются и в комнату входит второй игрок. Второй игрок также может открыть две из трех дверей, но не может ни в какой форме общаться с первым игроком. Какова вероятность победы, если оба игрока действуют оптимально?

Если игроки выбирают свои двери случайным образом, вероятность выигрыша составляет всего ⁠ 4/9 ⁠ ( около 44% ) . Однако оптимальная стратегия заключается в следующем:

• Игрок 1 первым открывает дверь 1. Если машина находится за дверью, игрок добился успеха. Если ключи находились за дверью, игрок затем открывает дверь 2; если вместо этого коза была за дверью, игрок затем открывает дверь 3.
• Игрок 2 первым открывает дверь 2. Если ключи находятся за дверью, игрок добился успеха. Если коза была за дверью, игрок затем открывает дверь 3; тогда как, если машина находилась за дверью, игрок затем открывает дверь 1.

В шести возможных распределениях машины, ключей и козла за тремя дверями игроки открывают следующие двери (в зеленых случаях игрок добился успеха):

	Машина — Ключи — Коза	Автомобиль — Коза — Ключи	Ключи — Машина — Коза	Ключи — Коза — Автомобиль	Коза — Машина — Ключи	Коза — Ключи — Автомобиль
Игрок 1	Дверь 1: Автомобиль	Дверь 1: Автомобиль	Дверь 1: Ключи Дверь 2: Автомобиль	Дверь 1: Ключи Дверь 2: Коза	Дверь 1: Коза Дверь 3: Ключи	Дверь 1: Коза Дверь 3: Автомобиль
Игрок 2	Дверь 2: Ключи	Дверь 2: Коза Дверь 3: Ключи	Дверь 2: Автомобиль Дверь 1: Ключи	(Дверь 2: Коза) (Дверь 3: Автомобиль)	(Дверь 2: Автомобиль) (Дверь 1: Коза)	Дверь 2: Ключи

Успех стратегии основан на построении корреляции между успехами и неудачами двух игроков. Здесь вероятность выигрыша равна ⁠ 2 / 3 ⁠ , что является оптимальным, поскольку первый игрок не может иметь более высокую вероятность выигрыша, чем эта. В дальнейшем варианте три приза спрятаны за тремя дверями, и три игрока должны самостоятельно найти назначенные им призы с двух попыток. В этом случае вероятность выигрыша также равна ⁠ 2 / 3 ⁠ при использовании оптимальной стратегии.

Нечетное количество попыток

Вместо того, чтобы находить их количество в первых 50 попытках, тест может заключаться в поиске числа в 50 попытках с нечетными номерами: 1, 3, ..., 97, 99 . Любой заключенный имеет 50% шанс найти свой номер при попытке с нечетным номером. Основная стратегия будет работать для всех заключенных, если перестановка заключенных содержит только циклы нечетной длины. Для 100 заключенных вероятность того, что все добьются успеха, используя основную стратегию, составляет примерно 7,9589%, что существенно выше вероятности (1/2). ¹⁰⁰ это было бы получено, если бы каждый заключенный открывал ящики самостоятельно и наугад.

См. также

• Дилемма заключенного
• Проблема трех заключенных
• Неожиданный парадокс зависания
• Статистика случайных перестановок
• Постоянная Голомба – Дикмана

Литература

• Филипп Флажоле , Роберт Седжвик (2009), Аналитическая комбинаторика , Издательство Кембриджского университета, ISBN  978-1-139-47716-1
• Ричард П. Стэнли (2013), Алгебраическая комбинаторика: прогулки, деревья, таблицы и многое другое , Тексты для студентов по математике , Springer, ISBN  978-1-461-46998-8
• Питер Винклер (2007), Математические повелители разума , Тейлор и Фрэнсис, ISBN  978-1-568-81336-3

Внешние ссылки

• Роб Хитон: Математики ненавидят гражданские свободы – 100 заключенных и 100 ящиков , 13 января 2014 г.
• Оливер Нэш: Пожалейте заключенных. Архивировано 14 июля 2014 г. в Wayback Machine , 12 декабря 2009 г.
• Джейми Малхолланд: Узники в коробках , весна 2011 г. (PDF)
• MinutePhysics : Невозможная ставка на YouTube и решение невозможной ставки на YouTube , 8 декабря 2014 г.
• Роберт Фельдт: Стохастическое моделирование в Джулии для проверки оптимальной стратегии, 6 июля 2022 г.