Нелинейная теория полупроводниковых лазеров

Лазерная теория Фабри-Перо (ФП) полупроводниковых лазеров оказывается нелинейной, поскольку усиления коэффициент показатель преломления и коэффициент потерь являются функциями потока энергии . Нелинейная теория позволил объяснить ряд экспериментов, некоторые из которых даже невозможно было объяснить (например, естественная ширина линии ), а тем более смоделировать на основе других теоретических моделей; это позволяет предположить, что разработанная нелинейная теория представляет собой новую парадигму теории лазеров.

Уравнения в усиливающей среде

Уравнения Максвелла описывают поле для пассивной среды и не могут быть использованы для описания поля в лазере и квантовом усилителе . Выведены феноменологические уравнения для электромагнитного поля в активной среде , т.е. уравнения Максвелла для активной среды и теорема Пойнтинга для этих уравнений. Уравнения Максвелла в усиливающей среде используются для получения уравнений потока энергии и для описания нелинейного фазового эффекта.

$(1)\quad rot{\vec {H}}=(\sigma -\eta ){\vec {E}}+{\partial {\vec {D}} \over \partial t},$
мы определили η как определенный коэффициент усиления; σ — удельная проводимость , описывающая некогерентные потери (например, на свободных электронах). Остальные уравнения Максвелла используются без изменений.
$(2)\quad rot{\vec {E}}=-{\partial B \over \partial t},divD=0,divB=0,$
$(3)\quad D=\epsilon '\epsilon _{0}E,B=\mu _{0}\mu H,$
Теорема Пойнтинга следует из (1)-(3):
$(4)\quad \int _{V}\eta |E(\omega )|^{2}\,dv=\int _{V}\sigma |E(\omega )|^{2}\,dv+\oint _{S}(Sn)ds,$

где S – вектор Пойнтинга ; V=sz, 0 <z<L, где s — поперечное сечение (по оси z) активной лазерной среды .
Уравнения для потока энергии следуют из (4):
$(5)\quad {\frac {dI^{+}}{dz}}=(\Gamma g(I^{+})-\alpha (I^{+}))I^{+},$
$(6)\quad {\frac {-dI^{-}}{dz}}=(\Gamma g(I^{-})-\alpha (I^{-}))I^{-},$
где
$(7)\quad \alpha (I)=(1-\Gamma )\alpha _{out}+\Gamma \alpha _{in}+\alpha _{x}+\alpha _{2p}(I),$
где $I$ – поток энергии; $s$ – площадь сечения активной зоны лазера; $\Gamma$ – коэффициент удержания; $\alpha _{in}$ – коэффициент поглощения в активной зоне; $\alpha _{out}$ – коэффициент поглощения вне активной зоны; $\alpha _{x}$ – потери из-за некогерентного рассеяния ; $\alpha _{2p}(I)$ – коэффициент двухфотонного поглощения; и $\alpha _{2p}(I)=\beta \cdot I$).

Формулы формы линии и естественной ширины линии

Разработана теория естественной ширины линии полупроводниковых лазеров, из которой следует, что показатель преломления n в ФП-лазерах и эффективный показатель преломления n _ef в лазерах с распределенной обратной связью (DFB) являются функциями E:
$(8)\quad n=n_{0}+n_{1}(\omega )E+n_{2}(\omega )E^{2},$
$(9)\quad n=n_{ef}^{0}+n_{ef}^{1}E+n_{ef}^{2}E^{2},$
Выведены формулы для формы линии в ФП и DFB лазерах. Эти формулы формы линии аналогичны и имеют следующий вид:
$(10)\quad L(v)=2\int _{0}^{\infty }\cos(2\pi v\tau )exp(A_{pa}|\tau |-B\tau ^{2})d\tau ,$
где $v={\tfrac {\omega -\omega L}{2\pi }};\quad \omega L$ – частота генерации лазера;

$(11)\quad A_{pa}={\frac {D_{0}}{P}},\quad B=(D_{1}+D_{2}P^{(1/2)})^{2},$
где $D_{0},D_{1},andD_{2}$ имеют разную форму для ФП и для DFB лазеров . Запишем естественную ширину линии Δν
$(12)\quad \Delta v=\Delta v^{(c)}T\left(\left(mW\right){\frac {A_{pa}}{P}}+B\right)F_{N}\left({\frac {P^{(c)}}{P}},k\right),$
где $T\left(\left(mW\right){\frac {A_{pa}}{P}}+B\right)$ – мостовая функция; $\Delta v^{(c)}$ и $P^{(c)}$ – характерная ширина линии и характерная мощность лазера; k – характерный параметр нелинейности лазера; q — безразмерная обратная степень:

$(13)\quad F_{N}(q,k)=1/\int _{0}^{\infty }exp(-xq-x^{2}(k/q^{1/2}-1)^{2})dx$

Самостоятельное значение имеет теория естественной ширины линии полупроводниковых лазеров. В то же время разработанная теория является неотъемлемой частью нелинейной теории лазеров, а ее понятия и введенные характеристические параметры используются во всех разделах нелинейной теории.

Усиление полупроводникового лазера

Используя уравнения матрицы плотности с релаксацией, были сделаны следующие выводы: спектральный коэффициент Эйнштейна в полупроводниковом лазере и, соответственно, коэффициент Эйнштейна ; получена формула эффекта насыщения в полупроводниковом лазере; было показано, что эффект насыщения в полупроводниковом лазере мал. Коэффициент усиления полупроводникового лазера получен с использованием уравнений матрицы плотности с релаксацией. Было обнаружено, что усиление лазера Фабри-Перо зависит от потока энергии, и это определяет «основной нелинейный эффект» в полупроводниковом лазере.

$(14)\quad g=g(I)=R\Delta \omega _{e}/(1-I(\delta \Delta \omega _{e}/\delta I)/\Delta \omega _{e}),$

где
$(15)\quad R=(\hbar \omega n_{g}/c)B_{21}(f_{2}-f_{1})S_{P}(\omega ).$

где $B_{21}$ коэффициент Эйнштейна для индуцированного перехода между двумя уровнями энергии при воздействии узкополосной волны записывается в следующем виде:
$(16)\quad B_{21}=({\hat {H}}_{21}/\hbar )^{2}/(2\Gamma _{0})$ где $\Delta \omega _{e}$ – эффективная естественная ширина линии; $I$ – поток энергии; $S_{P}(\omega )$ – спектральная плотность переходов.

Необходимое условие наведенного излучения 1-го рода.

Необходимые условия возникновения наведенного излучения 1-го и 2-го рода определены в . Необходимые условия наведенного излучения определяются требованием, чтобы коэффициент усиления был больше нуля. Необходимое условие наведенного излучения 1-го рода, сформулированное Бернаром и Дюраффуром. заключается в том, что население уровней, расположенных выше, становится больше, чем население уровней, расположенных ниже.

$(17)\quad f_{2}(E_{2})>f_{1}(E_{1}).$

Необходимое условие наведенного излучения 2-го рода.

Необходимое условие наведенного излучения 2-го рода, сформулированное Ноппе это что:

$(18)\quad \Delta \omega _{e}/(1-I(\delta \Delta \omega _{e}/\delta I)/\Delta \omega _{e})>0.$

Рисунок.1. Функции $g_{1}(I)$ и $g_{2}(I)$ от потока энергии I для двух наборов характеристических параметров.

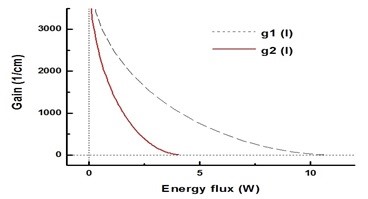
Необходимое условие наведенного излучения 2-го рода позволяет сформулировать основное ограничение мощности лазера: что подтверждено экспериментально:

$(19)\quad I<I(M),$

где $I$ – поток энергии; $I(M)$ – характерный параметр предельной мощности. На рисунке 1 показана функция $g(I)$ для двух наборов характеристических параметров.

Моделирование экспериментов

4.1. Уравнения Максвелла в усиливающей среде используются для получения уравнений потока энергии. Нелинейный фазовый эффект был описан и смоделирован. используя нелинейность показателя преломления. (см. рис.3).

4.2. На основе разработанной теории были смоделированы экспериментальные выходные характеристики: естественная ширина линии (см. моделирование в ) (см. рис.2), экспериментальные ватт-амперные характеристики (см. рис.4) и зависимость экспериментальной длины линии выходного излучения от тока в полупроводниковых инжекционных лазерах Фабри-Перо, (см. рис.3), а также ширину линии в DFB-лазерах (см. моделирование в ). Созданная теория позволяет моделировать большинство опубликованных экспериментов по измерению естественной ширины линии в лазерах Фабри-Перо и DFB-лазерах с распределенной обратной связью. двумя методами (с использованием (13) и (15)). На основе формулы, полученной для формы линии, 12 экспериментов по измерению естественной ширины линии в лазерах Фабри-Перо (например, см. рис.2) и 15 экспериментов в DFB-лазерах. были смоделированы. На основе формулы, полученной для естественной ширины линии, 15 экспериментов по измерению естественной ширины линии в лазерах Фабри-Перо и 15 экспериментов в DFB-лазерах. были смоделированы. Выведенная формула для формы линии излучения (ФП-лазеров и DFB-лазеры ) отличается от формулы линии Лоренца.

4.3. На основе разработанной теории были смоделированы экспериментальные выходные характеристики: естественная ширина линии (см. моделирование в ), экспериментальные ватт-амперные характеристики (см. рис.4) и зависимость экспериментальной длины линии выходного излучения от тока в полупроводниковых инжекционных лазерах Фабри-Перо (см. рис.3), а также ширину линии в DFB-лазерах (см. моделирование в ).

4.4. На основе нелинейной теории даны рекомендации по созданию лазеров с меньшей естественной шириной линии и лазеров с большей выходной мощностью.

Рисунок.2. Моделирование экспериментальной кривой естественной ширины линии полупроводниковых лазеров Фабри-Перо в зависимости от обратной выходной мощности Δν _e (1/P ) (Ke=14) по теоретической кривой Δνe(1/P ) (К _т =14).

Рис. 3. Сдвиг длины волны Δλ (теоретический и экспериментальный ) по сравнению с нормализованным током (Дж/Джт)

Рисунок 4. Экспериментальная часть и теоретический выходная мощность в зависимости от тока для мощного лазера.

Заключение

На основе решения уравнений матрицы плотности получен коэффициент Эйнштейна для вынужденного перехода; показано, что эффект насыщения мал для полупроводниковых лазеров. Выведена формула выигрыша в зависимости от потока энергии; это основной нелинейный эффект в лазере. Было установлено, что основным эффектом, приводящим к нелинейности, является эффект насыщения. Для полупроводниковых лазеров эффект насыщения пренебрежимо мал. Коэффициент усиления g для полупроводникового лазера Фабри-Перо был получен нами на основе уравнений матрицы плотности и выражений для естественной ширины линии. Таким образом, теория ширины линии является неотъемлемой частью нелинейной теории. Полученная зависимость g от потока энергии получила название основного нелинейного эффекта в полупроводниковых лазерах; Вывод этой формулы соотношения представлен в . Экспериментальный сдвиг длины волны в зависимости от нормированного тока (J/Jth) и зависимости выходной мощности от тока были смоделированы для мощного лазера с квантовой ямой из собственного полупроводника. Учтено расширение плотности состояний из-за различных эффектов. Нелинейная теория позволила объяснить ряд экспериментов, некоторые из которых даже невозможно было объяснить (например, естественная ширина линии), а тем более смоделировать на основе других теоретических моделей; это позволяет предположить, что разработанная нелинейная теория представляет собой новую парадигму теории лазеров. В связи с развитием нелинейной теории могут быть даны рекомендации по созданию лазеров с меньшей естественной шириной линии и лазеров с большей выходной мощностью.