Гамильтонова разложение

В теории графов , разделе математики, гамильтоново разложение данного графа представляет собой разбиение ребер графа на гамильтоновы циклы . Гамильтоновы разложения изучались как для неориентированных, так и для ориентированных графов . В неориентированном случае гамильтоново разложение также можно описать как 2-факторизацию графа, при которой каждый фактор связен.

Необходимые условия

Чтобы гамильтоново разложение существовало в неориентированном графе, граф должен быть связным и регулярным четной степени .Ориентированный граф с таким разложением должен быть сильно связным , и все вершины должны иметь одинаковую входную и выходную степень, но эта степень не обязательно должна быть четной. ^[1]

Специальные классы графов

Полные графики

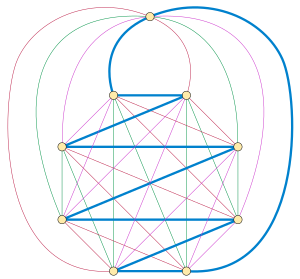
Каждый полный граф с нечетным числом $n$ вершин имеет гамильтоново разложение. Этот результат, который является частным случаем проблемы Обервольфаха о разложении полных графов на изоморфные 2-факторы, был приписан Валецкому Эдуардом Лукасом в 1892 году.Строительные площадки Валецкого $n-1$ вершин в правильный многоугольник и покрывает весь граф в этом подмножестве вершин с $(n-1)/2$ Гамильтоновы пути, которые зигзагообразно пересекают многоугольник, при этом каждый путь повернут относительно друг друга на кратное число $\pi /(n-1)$ .Тогда все пути можно завершить до гамильтоновых циклов, соединив их концы через оставшуюся вершину. ^[2]

Расширение вершины a $2k$ -регулярный граф клику в $2k$ вершины, по одной на каждую конечную точку ребра в заменяемой вершине, не могут изменить, имеет ли граф гамильтоново разложение. Обратный процесс расширения, сжимающий клику до одной вершины, преобразует любое гамильтоново разложение в большем графе в гамильтоново разложение в исходном графе. И наоборот, конструкция Валецкого может быть применена к клике для расширения любого гамильтонова разложения меньшего графа в гамильтоново разложение расширенного графа. ^[3]

Одним из аналогов полного графа в случае ориентированных графов является турнир . Это граф, в котором каждая пара различных вершин соединена одним направленным ребром, ведущим от одной к другой; например, такой график может описывать результат турнира по круговой системе по видам спорта, где каждый участник турнира играет друг с другом, а ребра направлены от проигравшего в каждой игре к победителю. Отвечая на гипотезу Пола Келли 1968 года, ^[4] Даниэла Кюн и Дерик Остус доказали в 2012 году, что каждый достаточно большой регулярный турнир имеет гамильтоново разложение. ^[5]

Планарные графы

Для 4-регулярных плоских графов дополнительные необходимые условия можно вывести из теоремы Гринберга . Примером 4-регулярного планарного графа, не удовлетворяющего этим условиям и не имеющего гамильтонова разложения, является медиальный граф графа Гершеля . ^[6]

Призмы

Нерешенная задача по математике :

Любая ли призма над 3-связным 3-регулярным графом имеет гамильтоново разложение?

(еще нерешенные задачи по математике)

Призма декартово над графом — это его произведение на полный двухвершинный граф. Например, призма над графом цикла является графиком геометрической призмы . 4-регулярные графы, полученные как призмы над 3-регулярными графами, были особенно изучены с точки зрения гамильтонова разложения. Когда базовый 3-регулярный граф является 3-вершинно-связным , результирующая 4-правильная призма всегда имеет гамильтонов цикл и, во всех проверенных примерах, гамильтоново разложение. Основываясь на этом наблюдении, Альспах и Розенфельд в 1986 году выдвинули гипотезу, что все призмы над 3-регулярными 3-связными графами имеют гамильтоново разложение. ^[7]^[8]

Известно, что многие классы 3-регулярных 3-связных графов имеют призмы с гамильтоновыми разложениями. В частности, это происходит, когда 3-регулярный граф является плоским и двудольным, когда он является графом Халина , когда он сам является призмой или лестницей Мёбиуса или когда он является обобщенным графом Петерсена порядка, кратного четырем. ^[8]^[9]

Симметричные графы

Существует бесконечно много вершинно-транзитивных графов (графов, в которых каждая вершина симметрична каждой другой вершине), которые не имеют гамильтонова разложения. В частности, это относится к графам Кэли , вершины которых описывают элементы группы , а элементы описывают умножение на образующие группы . Бесконечно многие 6-регулярные графы Кэли не имеют гамильтонова разложения, и существуют графы Кэли сколь угодно большой четной степени без гамильтонова разложения. Один из способов построения таких графов — использование повторяющихся разложений по кликам, которые сохраняют симметрию и не могут изменить существование гамильтонова разложения. ^[3]

Количество разложений

Любой 4-регулярный неориентированный граф имеет четное число гамильтоновых разложений. Более строго, для каждых двух ребер $e$ и $f$ 4-регулярного графа количество гамильтоновых разложений, в которых $e$ и $f$ принадлежат одному циклу, четны. Если $2k$ -регулярный граф имеет гамильтоново разложение, он имеет не менее тройного факториала разложений,

(3k-2)\cdot (3k-5)\cdots 7\cdot 4\cdot 1.

Например, 4-регулярные графы, имеющие гамильтоново разложение, имеют по крайней мере четыре из них; 6-регулярные графы, имеющие гамильтоново разложение, имеют не менее 28 и т. д.Отсюда следует, что единственные графы, гамильтоновы разложения которых единственны, — это графы циклов . ^[10]

Вычислительная сложность

Проверка того, имеет ли произвольный граф гамильтоново разложение, является NP-полной как в направленном, так и в неориентированном случаях. ^[11] В частности, вопрос является NP-полным для регулярных графов заданной четной степени; например, для 4-регулярных графов.

Линейные графы кубических графов являются 4-регулярными и имеют гамильтоново разложение тогда и только тогда, когда базовый кубический граф имеет гамильтонов цикл. ^[12]^[13] Как следствие, гамильтоново разложение остается NP-полным для классов графов, которые включают линейные графы жестких примеров гамильтоновой проблемы цикла . Например, гамильтоново разложение является NP-полным для 4-регулярных плоских графов, поскольку они включают линейные графы кубических плоских графов. С другой стороны, из этой эквивалентности также следует, что гамильтоново разложение легко для 4-регулярных линейных графов, когда лежащие в их основе кубические графы имеют простые проблемы гамильтоновых циклов.

Случайные регулярные графы четной степени почти наверняка имеют гамильтоново разложение, и, что более важно, существует рандомизированный алгоритм с полиномиальным временем , который, если на входе задан случайный регулярный граф четной степени, почти наверняка находит в нем гамильтоново разложение. ^[14]

См. также

Линейная древовидность , другой вид условного разделения на подграфы максимальной второй степени.

Ссылки

^ Бермонд, Ж.-К. (1978), «Гамильтоновы разложения графов, ориентированных графов и гиперграфов» , Annals of Discrete Mathematics , 3 : 21–28 , doi : 10.1016/S0167-5060(08)70494-1 , ISBN 9780720408430 , МР 0505807
^ Олспах, Брайан (2008), «Замечательная конструкция Валецкого», Бюллетень Института комбинаторики и ее приложений , 52 : 7–20, MR 2394738
^ Jump up to: ^а ^б Брайант, Дэррин; Дин, Мэтью (2015), «Вершинно-транзитивные графы, не имеющие разложения Гамильтона», Журнал комбинаторной теории , серия B, 114 : 237–246, arXiv : 1408.5211 , doi : 10.1016/j.jctb.2015.05.007 , MR 3354297
^ Мун, Джон В. (1968), Темы турниров , Нью-Йорк, Монреаль, Лондон: Холт, Райнхарт и Уинстон, Упражнение 9, стр. 9, MR 0256919
^ Кюн, Даниэла ; Остус, Дерик (2013), «Гамильтоновы разложения регулярных расширителей: доказательство гипотезы Келли для больших турниров», Advances in Mathematics , 237 : 62–146, arXiv : 1202.6219 , doi : 10.1016/j.aim.2013.01.005 , МР 3028574
^ Бонди, JA ; Хэггквист, Р. (1981), «Непересекающиеся по краям циклы Гамильтона в 4-регулярных плоских графах», Aequationes Mathematicae , 22 (1): 42–45, doi : 10.1007/BF02190157 , MR 0623315
^ Олспах, Брайан ; Розенфельд, Моше (1986), «О гамильтоновых разложениях призм по простым 3-многогранникам», Graphs and Combinatorics , 2 (1): 1–8, doi : 10.1007/BF01788070 , MR 1117125
^ Jump up to: ^а ^б Розенфельд, Моше; Сян, Цзицин (2014), «Гамильтоново разложение призм по кубическим графам», Discrete Mathematics & Theoretical Computer Science , 16 (2): 111–124, doi : 10.46298/dmtcs.2079 , MR 3349112
^ Чада, Роман; Кайзер, Тома; Розенфельд, Моше; Рыячек, Зденек (2004), «Гамильтоновы разложения призм по кубическим графам», Discrete Mathematics , 286 (1–2): 45–56, doi : 10.1016/j.disc.2003.11.044 , MR 2084278
^ Томасон, А.Г. (1978), «Гамильтоновы циклы и графы, раскрашиваемые однозначно по краям», Достижения в теории графов (Кембриджская комбинаторная конференция, Тринити-колледж, Кембридж, 1977) , Анналы дискретной математики, том. 3, стр. 259–268, МР 0499124
^ Перош, Б. (1984), «NP-полнота некоторых проблем разбиения и покрытия в графах», Discrete Applied Mathematics , 8 (2): 195–208, doi : 10.1016/0166-218X(84)90101-X , МР 0743024
^ Коциг, Антон (1957), «Из теории конечных регулярных графов третьей и четвертой степени», Časopis Pro Pěstování Matematiky , 82 : 76–92, MR 0090815
^ Мартин, Пьер (1976), «Гамильтоновы циклы в 4-регулярных 4-связных графах», Aequationes Mathematicae , 14 (1/2): 37–40, doi : 10.1007/BF01836203 , MR 0414442
^ Ким, Чон Хан ; Вормальд, Николас К. (2001), «Случайные сопоставления, которые вызывают гамильтоновые циклы и гамильтоновы разложения случайных регулярных графов», Журнал комбинаторной теории , серия B, 81 (1): 20–44, doi : 10.1006/jctb.2000.1991 , МР 1809424

[b-1] Бермонд, Ж.-К. (1978), «Гамильтоновы разложения графов, ориентированных графов и гиперграфов» , Annals of Discrete Mathematics , 3 : 21–28 , doi : 10.1016/S0167-5060(08)70494-1 , ISBN 9780720408430 , МР 0505807

[a-2] Олспах, Брайан (2008), «Замечательная конструкция Валецкого», Бюллетень Института комбинаторики и ее приложений , 52 : 7–20, MR 2394738

[bd-3] Jump up to: ^а ^б Брайант, Дэррин; Дин, Мэтью (2015), «Вершинно-транзитивные графы, не имеющие разложения Гамильтона», Журнал комбинаторной теории , серия B, 114 : 237–246, arXiv : 1408.5211 , doi : 10.1016/j.jctb.2015.05.007 , MR 3354297

[moon-4] Мун, Джон В. (1968), Темы турниров , Нью-Йорк, Монреаль, Лондон: Холт, Райнхарт и Уинстон, Упражнение 9, стр. 9, MR 0256919

[ko-5] Кюн, Даниэла ; Остус, Дерик (2013), «Гамильтоновы разложения регулярных расширителей: доказательство гипотезы Келли для больших турниров», Advances in Mathematics , 237 : 62–146, arXiv : 1202.6219 , doi : 10.1016/j.aim.2013.01.005 , МР 3028574

[bh-6] Бонди, JA ; Хэггквист, Р. (1981), «Непересекающиеся по краям циклы Гамильтона в 4-регулярных плоских графах», Aequationes Mathematicae , 22 (1): 42–45, doi : 10.1007/BF02190157 , MR 0623315

[ar-7] Олспах, Брайан ; Розенфельд, Моше (1986), «О гамильтоновых разложениях призм по простым 3-многогранникам», Graphs and Combinatorics , 2 (1): 1–8, doi : 10.1007/BF01788070 , MR 1117125

[rx-8] Jump up to: ^а ^б Розенфельд, Моше; Сян, Цзицин (2014), «Гамильтоново разложение призм по кубическим графам», Discrete Mathematics & Theoretical Computer Science , 16 (2): 111–124, doi : 10.46298/dmtcs.2079 , MR 3349112

[ckrr-9] Чада, Роман; Кайзер, Тома; Розенфельд, Моше; Рыячек, Зденек (2004), «Гамильтоновы разложения призм по кубическим графам», Discrete Mathematics , 286 (1–2): 45–56, doi : 10.1016/j.disc.2003.11.044 , MR 2084278

[t-10] Томасон, А.Г. (1978), «Гамильтоновы циклы и графы, раскрашиваемые однозначно по краям», Достижения в теории графов (Кембриджская комбинаторная конференция, Тринити-колледж, Кембридж, 1977) , Анналы дискретной математики, том. 3, стр. 259–268, МР 0499124

[p-11] Перош, Б. (1984), «NP-полнота некоторых проблем разбиения и покрытия в графах», Discrete Applied Mathematics , 8 (2): 195–208, doi : 10.1016/0166-218X(84)90101-X , МР 0743024

[k-12] Коциг, Антон (1957), «Из теории конечных регулярных графов третьей и четвертой степени», Časopis Pro Pěstování Matematiky , 82 : 76–92, MR 0090815

[m-13] Мартин, Пьер (1976), «Гамильтоновы циклы в 4-регулярных 4-связных графах», Aequationes Mathematicae , 14 (1/2): 37–40, doi : 10.1007/BF01836203 , MR 0414442

[kw-14] Ким, Чон Хан ; Вормальд, Николас К. (2001), «Случайные сопоставления, которые вызывают гамильтоновые циклы и гамильтоновы разложения случайных регулярных графов», Журнал комбинаторной теории , серия B, 81 (1): 20–44, doi : 10.1006/jctb.2000.1991 , МР 1809424

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]