Граф Гершеля
| Граф Гершеля | |
|---|---|
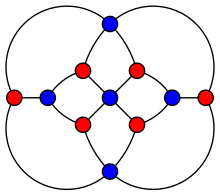 График Гершеля. | |
| Назван в честь | Александр Стюарт Гершель |
| Вершины | 11 |
| Края | 18 |
| Автоморфизмы | 12 ( Д 6 ) |
| Характеристики | |
| Таблица графиков и параметров | |
В теории графов , разделе математики , граф Гершеля представляет собой двудольный неориентированный граф с 11 вершинами и 18 ребрами. Это многогранный граф (график выпуклого многогранника ) и наименьший многогранный граф, не имеющий гамильтонова цикла , цикла, проходящего через все его вершины. Он назван в честь британского астронома Александра Стюарта Гершеля из-за исследований Гершелем гамильтоновых циклов в многогранных графах (но не в этом графе).
Определение и свойства
[ редактировать ]Граф Гершеля имеет три вершины четвертой степени (три синие вершины, выровненные вертикально в центре иллюстрации) и восемь вершин третьей степени. Каждые две различные вершины четвертой степени имеют общих двух соседей третьей степени, образуя цикл из четырех вершин с этими общими соседями. Таких циклов три, проходящих через шесть из восьми вершин третьей степени (красные на иллюстрации). Еще две вершины третьей степени (синие) не участвуют в этих четырехвершинных циклах; вместо этого каждая из них примыкает к трем из шести красных вершин. [1]
Граф Гершеля является многогранным графом ; это означает, что это планарный граф , который можно нарисовать на плоскости так, чтобы ни одно из его ребер не пересекалось, и что он 3-связен : удаление любых двух его вершин оставляет связный подграф . [1] Это двудольный граф : когда он раскрашен пятью синими и шестью красными вершинами, как показано на рисунке, каждое ребро имеет одну красную конечную точку и одну синюю конечную точку. [2]
Он имеет диэдральную симметрию 6-го порядка , всего 12 членов его группы автоморфизмов . Вершины четвертой степени можно переставлять произвольно, что дает шесть перестановок, и, кроме того, для каждой перестановки вершин четвертой степени существует симметрия, которая удерживает эти вершины фиксированными и меняет пары вершин третьей степени. [1]
Многогранник
[ редактировать ]По теореме Стейница каждый планарный и 3-связный граф имеет выпуклый многогранник которого является граф , скелетом . [3] Поскольку граф Гершеля обладает этими свойствами, [1] таким образом его можно представить в виде выпуклого многогранника, эннеаэдр, имеющий многогранник, имеет в качестве граней девять четырехугольников. [4] Это можно выбрать так, чтобы каждый автоморфизм графа соответствовал симметрии многогранника, и в этом случае три грани будут ромбами или квадратами, а остальные шесть — воздушными змеями . [1]
Двойственный многогранник представляет собой выпрямленную треугольную призму , которая может быть образована как выпуклая оболочка середин ребер треугольной призмы . Построенная таким образом, она имеет три квадратных грани в тех же плоскостях, что и квадратные грани призмы, две равносторонние треугольные грани в плоскостях треугольных концов призмы и еще шесть равнобедренных треугольных граней. Этот многогранник обладает тем свойством, что его грани нельзя пронумеровать так, чтобы на соседних гранях появлялись последовательные числа, и так, чтобы первое и последнее числа находились также на соседних гранях, поскольку такая нумерация обязательно соответствовала бы гамильтонову циклу в График Гершеля. Нумерация многогранных граней этого типа используется в качестве «счетчиков жизней с вращением» в игре Magic: The Gathering для отслеживания жизней игроков путем поворота многогранника к соседней грани всякий раз, когда жизнь потеряна. Карта в игре, Лич, позволяет игрокам вернуться из почти потерянного состояния с одной жизнью к исходному количеству жизней. Поскольку двойственный многогранник для графа Гершеля нельзя пронумеровать так, чтобы этот шаг соединял соседние грани, Константинидес и Константинидес (2018) называют каноническую многогранную реализацию этого двойственного многогранника «заклятым врагом Лича». [5]
гамильтоновость
[ редактировать ]
Будучи двудольным графом с нечетным числом вершин, граф Гершеля не содержит гамильтонова цикла (цикла ребер, проходящего через каждую вершину ровно один раз). Ибо в любом двудольном графе любой цикл должен чередовать вершины по обе стороны от двудольного графа и, следовательно, должен содержать равное количество вершин обоих типов и должен иметь четную длину. Таким образом, в графе Гершеля не может существовать цикл, проходящий один раз через каждую из одиннадцати вершин. Граф называется гамильтоновым, если он содержит гамильтонов цикл, поэтому граф Гершеля не является гамильтоновым. Он имеет наименьшее количество вершин, наименьшее количество ребер и наименьшее количество граней среди всех негамильтоновых многогранных графов. [6] Существуют и другие многогранные графы с 11 вершинами и без гамильтоновых циклов (в частности, граф Гольднера – Харари ). [7] но ни один с меньшим количеством ребер. [6]
Все вершины графа Гершеля, кроме трёх, имеют степень три. Граф называется кубическим или 3-регулярным , если все его вершины имеют степень три. П.Г. Тейт предположил [8] что многогранный 3-регулярный граф должен быть гамильтоновым; это было опровергнуто, когда У.Т.Татте привел контрпример — граф Тутте , который намного больше графа Гершеля. [9] Уточнение гипотезы Тейта, гипотезы Барнетта о том, что каждый двудольный 3-правильный многогранный граф является гамильтоновым, остается открытым. [10]
Каждый максимальный планарный граф , не имеющий гамильтонова цикла, имеет в качестве минора граф Гершеля . Предполагается, что граф Гершеля является одним из трех минорно-минимальных негамильтоновых 3-связных графов. Два других представляют собой полный двудольный граф. и граф, образованный путем разделения графа Гершеля и на две симметричные половины с помощью трехвершинных разделителей и последующего объединения по половине каждого графа. [11]

Граф Гершеля также представляет собой пример многогранного графа, для которого медиальный граф не имеет гамильтонового разложения на два гамильтоновых цикла, не пересекающихся по ребрам. Медиальный граф графа Гершеля представляет собой 4- регулярный граф с 18 вершинами, по одной на каждое ребро графа Гершеля; две вершины смежны в медиальном графе, если соответствующие ребра графа Гершеля последовательны на одной из его граней. [12] Он 4-вершинно-связен и, по существу, 6-реберно-связен . Здесь график -вершинно-связный или -реберно-связным, если при удалении менее вершины или ребра (соответственно) не могут его отключить. Плоские графы не могут быть 6-реберно-связными, поскольку они всегда имеют вершину степени не выше пяти, а удаление соседних ребер разъединяет граф. Терминология «по сути 6-реберной связи» означает, что этот тривиальный способ отключения графа игнорируется, и невозможно разделить граф на два подграфа, каждый из которых имеет не менее двух вершин, путем удаления пяти или меньшего количества ребер. [13]
История
[ редактировать ]График Гершеля назван в честь Александра Стюарта Гершеля , британского астронома, написавшего раннюю статью об Уильяма Роуэна Гамильтона икосианской игре . Это головоломка, связанная с поиском гамильтоновых циклов в многограннике, обычно в правильном додекаэдре . Граф Гершеля описывает наименьший выпуклый многогранник , который можно использовать вместо додекаэдра, чтобы получить игру, не имеющую решения. В статье Гершеля описаны решения икосианской игры только на графах правильного тетраэдра и правильного икосаэдра ; он не описывал граф Гершеля. [14] Название «граф Гершеля» впервые появляется в учебнике по теории графов Джона Адриана Бонди и USR Murty , опубликованном в 1976 году. [15] Сам граф был описан ранее, например, HSM Coxeter . [4]
Ссылки
[ редактировать ]- ^ Перейти обратно: а б с д и Лоусон-Перфект, Кристиан (13 октября 2013 г.), «Эннеаэдр для Гершеля» , The A periodical , получено 7 декабря 2016 г.
- ^ Холтон, Д.А. (1983), «Циклы в графах», в Кассе, LRA (ред.), Комбинаторная математика X: Материалы конференции, состоявшейся в Аделаиде, Австралия, 23–27 августа 1982 г. , Конспекты лекций по математике, том. 1036, Берлин: Springer, стр. 24–48, номер doi : 10.1007/BFb0071507 , ISBN. 978-3-540-12708-6 , МР 0731570
- ^ Грюнбаум, Бранко (2003), «13.1 Теорема Стейница», Выпуклые многогранники , Тексты для выпускников по математике , том. 221 (2-е изд.), Springer-Verlag, стр. 235–244, ISBN. 0-387-40409-0
- ^ Перейти обратно: а б Коксетер, HSM (1948), Правильные многогранники , Лондон: Метуэн, стр. 8
- ^ Константинидес, Энтони Ф.; Константинидес, Джордж А. (октябрь 2018 г.), «Многогранники со спинированием», The Mathematical Gazette , 102 (555): 447–453, doi : 10.1017/mag.2018.111 , S2CID 233357977
- ^ Перейти обратно: а б Барнетт, Дэвид; Юкович, Эрнест (1970), «Гамильтоновы схемы на 3-многогранниках», Журнал комбинаторной теории , 9 (1): 54–59, doi : 10.1016/S0021-9800(70)80054-0 .
- ^ Гольднер, А.; Харари, Ф. (1975), «Замечание о наименьшем негамильтоновом максимальном плоском графе», Bull. Малазийская математика. Соц. , 6 (1): 41–42 ; см. также тот же журнал 6 (2):33 (1975) и 8 :104-106 (1977). Ссылка из списка публикаций Харари .
- ^ Тейт, П.Г. (1884), Листинга « Топология » , Философский журнал , 5-я серия, 17 : 30–46 ; см. параграф (16), стр. 41–42. Перепечатано в Scientific Papers , вып. II, стр. 85–98.
- ^ Тутте, WT (1946), «О гамильтоновых схемах», Журнал Лондонского математического общества , 21 (2): 98–101, doi : 10.1112/jlms/s1-21.2.98
- ^ Шамаль, Роберт (11 июня 2007 г.), гипотеза Барнетта , Открытый сад проблем , получено 24 февраля 2011 г.
- ^ Дин, Гуоли; Маршалл, Эмили (2018), «Минимальный -связные негамильтоновы графы», Graphs and Combinatorics , 34 (2): 289–312, doi : 10.1007/s00373-018-1874-z , MR 3774453 , S2CID 253891751
- ^ Бонди, JA ; Хэггквист, Р. (1981), «Непересекающиеся по краям циклы Гамильтона в 4-регулярных плоских графах», Aequationes Mathematicae , 22 (1): 42–45, doi : 10.1007/BF02190157 , S2CID 120729891 .
- ^ Кирай, Чаба; Петерфальви, Ференц (2012), «Сбалансированные общие схемы без длинных путей», Discrete Mathematics , 312 (15): 2262–2271, doi : 10.1016/j.disc.2012.03.031 , MR 2926099
- ^ Гершель, А.С. (1862), «Икосова игра сэра У. Гамильтона» , Ежеквартальный журнал чистой и прикладной математики , 5 : 305
- ^ Бонди, JA ; Мурти, USR (1976), Теория графов с приложениями , Северная Голландия, стр. 53, МР 0411988



