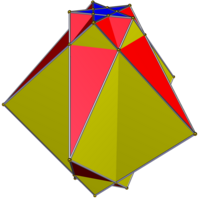
Выпрямленная призма

Набор выпрямленных призм
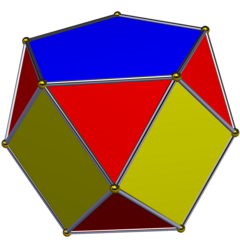Выпрямленная пятиугольная призма
Обозначение многогранника Конвея	ап н
Лица	2 н - кайф n квадратов 2 n треугольников
Края	6 н
Вершины	33н
Группа симметрии	D n h , [2,2 n ], (*22 n ), порядок 4 n
Группа вращения	Д н , [2, н ] + , (22 n ), порядок 2 n
Двойной многогранник	Объединенная призма
Характеристики	выпуклый

В геометрии ( выпрямленная призма выпрямленная бипирамида ) — один из бесконечного множества многогранников , построенный как выпрямление призмы n -угольной также , усекающий вершины до середины исходных ребер. В обозначениях многогранников Конвея он представлен как aPn , амбо-призма. Боковые квадраты или прямоугольные грани призмы становятся квадратами или ромбическими гранями, а новые грани равнобедренного треугольника представляют собой усечения исходных вершин.

Элементы

n n -угольная форма имеет 3 n вершин, 6 n ребер и 2+3 граней : 2 правильных n -угольника, n ромбов и 2 n треугольников.

Формы

Выпрямленная квадратная призма аналогична полуправильному кубооктаэдру .

н	3	4	5	6	7	н
Изображение
Сеть
Связанный		Кубооктаэдр

Также существуют выпрямленные звездчатые призмы, например, формы 5/2:

Двойной

Набор соединенных призм
Объединенная пятиугольная призма
Обозначение многогранника Конвея	Япония ​
Лица	33н
Края	6 н
Вершины	2+3 н
Группа симметрии	D n h , [2,2 n ], (*22 n ), порядок 4 n
Группа вращения	Д н , [2, н ] + , (22 n ), порядок 2 n
Двойной многогранник	Выпрямленная призма Выпрямленная бипирамида
Характеристики	выпуклый

Двойственной выпрямленной призме является соединенная призма или соединенная бипирамида в обозначениях многогранника Конвея . Операция соединения добавляет вершины в центры граней и заменяет ребра ромбическими гранями между исходным и соседним центрами граней. Объединенная квадратная призма имеет ту же топологию, что и ромбический додекаэдр . Объединенная треугольная призма представляет собой граф Гершеля .

н	3	4	5	6	8	н
Изображение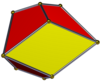
Сеть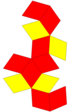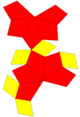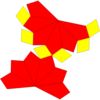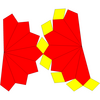
Связанный		Ромбический додекаэдр

См. также

• Выпрямленная антипризма

Внешние ссылки

• Обозначение Конвея для многогранников Попробуйте: aP n и jP n , где n =3,4,5,6... пример aP4 — выпрямленная квадратная призма, а jP4 — соединенная квадратная призма.