Переменные Мандельштама

На этой диаграмме две частицы входят с импульсами p ₁ и p ₂ , взаимодействуют каким-то образом, а затем уходят две частицы с разными импульсами (p ₃ и p ₄ ).

В теоретической физике представляют переменные Мандельштама собой числовые величины, которые кодируют энергию , импульс и углы частиц в процессе рассеяния лоренц-инвариантным способом. Они используются для процессов рассеяния двух частиц на две частицы. Переменные Мандельштама были впервые введены физиком Стэнли Мандельштамом в 1958 году.

Если метрика Минковского выбрана $\mathrm {diag} (1,-1,-1,-1)$ , переменные Мандельштама $s,t,u$ затем определяются

$s=(p_{1}+p_{2})^{2}c^{2}=(p_{3}+p_{4})^{2}c^{2}$
$t=(p_{1}-p_{3})^{2}c^{2}=(p_{4}-p_{2})^{2}c^{2}$
$u=(p_{1}-p_{4})^{2}c^{2}=(p_{3}-p_{2})^{2}c^{2}$ ,

где p ₁ и p ₂ — четырехимпульсы входящих частиц, а p ₃ и p ₄ — четырехимпульсы вылетающих частиц.

$s$ также известен как квадрат энергии центра масс ( инвариантной массы ) и $t$ как квадрат передачи четырехимпульса .

Диаграммы Фейнмана

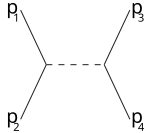
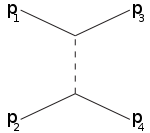
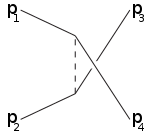
Буквы s,t,u также используются в терминах s-канал (времяподобный канал), t-канал и u-канал (оба пространственноподобных канала). Эти каналы представляют собой различные диаграммы Фейнмана или различные возможные события рассеяния, где взаимодействие включает обмен промежуточной частицей, квадрат четырехимпульса которой равен s,t,u соответственно.


s-канал	Т-канал	u-канал

Например, s-канал соответствует частицам 1,2, объединяющимся в промежуточную частицу, которая в конечном итоге разделяется на 3,4: s-канал — единственный способ резонансов и новых нестабильных частиц обнаружения при условии, что их время жизни достаточно велико. что они непосредственно обнаруживаются. ^{[ нужна ссылка ]} Т-канал представляет собой процесс, в котором частица 1 испускает промежуточную частицу и становится конечной частицей 3, а частица 2 поглощает промежуточную частицу и становится 4. U-канал — это t-канал с ролью частиц 3,4 поменялись местами.

При оценке амплитуды Фейнмана часто обнаруживаются скалярные произведения четырех внешних импульсов. Чтобы упростить их, можно использовать переменные Мандельштама:

$p_{1}\cdot p_{2}={\frac {s/c^{2}-m_{1}^{2}-m_{2}^{2}}{2}}$

$p_{1}\cdot p_{3}={\frac {m_{1}^{2}+m_{3}^{2}-t/c^{2}}{2}}$

$p_{1}\cdot p_{4}={\frac {m_{1}^{2}+m_{4}^{2}-u/c^{2}}{2}}$

Где $m_{i}$ - масса частицы с соответствующим импульсом $p_{i}$ .

Сумма

Обратите внимание, что

(s+t+u)/c^{4}=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}

где m _i — масса частицы i . ^[1]

Доказательство

Чтобы доказать это, нам нужно использовать два факта:

Квадрат четырех импульсов частицы равен квадрату ее массы.

p_{i}^{2}=m_{i}^{2}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (1)

И сохранение четырехимпульса,

p_{1}+p_{2}=p_{3}+p_{4}

p_{1}=-p_{2}+p_{3}+p_{4}\quad \quad \quad \quad \quad \quad \,\,(2)

Итак, для начала

s/c^{2}=(p_{1}+p_{2})^{2}=p_{1}^{2}+p_{2}^{2}+2p_{1}\cdot p_{2}

t/c^{2}=(p_{1}-p_{3})^{2}=p_{1}^{2}+p_{3}^{2}-2p_{1}\cdot p_{3}

u/c^{2}=(p_{1}-p_{4})^{2}=p_{1}^{2}+p_{4}^{2}-2p_{1}\cdot p_{4}

Затем добавление трех при вставке квадратов масс приводит к:

(s+t+u)/c^{2}=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}+2p_{1}^{2}+2p_{1}\cdot p_{2}-2p_{1}\cdot p_{3}-2p_{1}\cdot p_{4}

Затем обратите внимание, что последние четыре члена в сумме дают ноль благодаря сохранению четырехимпульса:

2p_{1}^{2}+2p_{1}\cdot p_{2}-2p_{1}\cdot p_{3}-2p_{1}\cdot p_{4}=2p_{1}\cdot (p_{1}+p_{2}-p_{3}-p_{4})=0

Итак, наконец,

(s+t+u)/c^{2}=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}

.

Релятивистский предел

В релятивистском пределе импульс (скорость) велик, поэтому, используя релятивистское уравнение энергии-импульса , энергия становится по существу нормой импульса (например, $E^{2}=\mathbf {p} \cdot \mathbf {p} +{m_{0}}^{2}$ становится $E^{2}\approx \mathbf {p} \cdot \mathbf {p}$ ). Остальной массой также можно пренебречь.

Так, например,

s/c^{2}=(p_{1}+p_{2})^{2}=p_{1}^{2}+p_{2}^{2}+2p_{1}\cdot p_{2}\approx 2p_{1}\cdot p_{2}

потому что $p_{1}^{2}=m_{1}^{2}$ и $p_{2}^{2}=m_{2}^{2}$ .

Таким образом,

$s/c^{2}\approx$	$2p_{1}\cdot p_{2}\approx$	$2p_{3}\cdot p_{4}$
$t/c^{2}\approx$	$-2p_{1}\cdot p_{3}\approx$	$-2p_{2}\cdot p_{4}$
$u/c^{2}\approx$	$-2p_{1}\cdot p_{4}\approx$	$-2p_{3}\cdot p_{2}$