Теорема Нортона

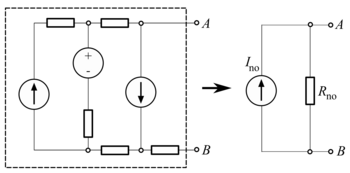
текст — Любой черный ящик, содержащий только сопротивления и *источники напряжения и тока, можно заменить эквивалентной схемой,* состоящей из эквивалентного источника тока, подключенного параллельно с эквивалентным сопротивлением.

В постоянного тока теории цепей , теорема Нортона также называемая теоремой Майера-Нортона , представляет собой упрощение, которое может быть применено к сетям, состоящим из линейных, не зависящих от времени сопротивлений , источников напряжения и источников тока . На паре клемм сети его можно заменить источником тока и параллельно включенным одиночным резистором.

Для систем переменного тока (AC) теорема может быть применена как к реактивным импедансам, так и к сопротивлениям.

Эквивалентная схема Нортона используется для представления любой сети линейных источников и импедансов на заданной частоте .

Теорема Нортона и двойственная ей теорема Тевенена широко используются для упрощения анализа цепей и изучения начального состояния схемы и установившегося отклика.

Теорема Нортона была независимо выведена в 1926 году Siemens & Halske исследователем Гансом Фердинандом Майером (1895–1980) и Bell Labs инженером Эдвардом Лоури Нортоном (1898–1983). ^{[ 1 ]}^{[ 2 ]}^{[ 3 ]}^{[ 4 ]}^{[ 5 ]}^{[ 6 ]}

Чтобы найти эквивалент, ток Нортона I _no рассчитывается как ток, текущий на клеммах короткого замыкания (нулевое сопротивление между A и B ). Это я _нет . Сопротивление Нортона R _no определяется путем расчета выходного напряжения, создаваемого без подключения сопротивления к клеммам; эквивалентно, это сопротивление между клеммами со всеми (независимыми) источниками напряжения, короткозамкнутыми и независимыми источниками тока, разомкнутыми . Это эквивалентно расчету сопротивления Тевенина.

При наличии зависимых источников необходимо использовать более общий метод. Напряжение на клеммах рассчитано для подачи на клеммы испытательного тока силой 1 А. Это напряжение, разделенное на ток 1 А, представляет собой импеданс Нортона R _no (в Омах). Этот метод необходимо использовать, если в цепи имеются зависимые источники, но его можно использовать во всех случаях, даже когда зависимых источников нет.

Пример эквивалентной схемы Нортона

Оригинальная схема
Расчет эквивалентного выходного тока
Расчет эквивалентного сопротивления
Спроектируйте эквивалентную схему Нортона

В этом примере общий ток I _total определяется как:

I_{\mathrm {total} }={15\,\mathrm {V}  \over 2\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \parallel (1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega )}=5.625\,\mathrm {mA} .

Тогда ток через нагрузку, используя правило делителя тока :

{\begin{aligned}I_{\mathrm {no} }&={1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega  \over 1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega }\cdot I_{\mathrm {total} }\\[5pt]&=2/3\cdot 5.625\,\mathrm {mA} =3.75\,\mathrm {mA} .\end{aligned}}

И эквивалентное сопротивление, если посмотреть на цепь, равно:

R_{\mathrm {no} }=1\,\mathrm {k} \Omega +(2\,\mathrm {k} \Omega \parallel (1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega ))=2\,\mathrm {k} \Omega .

Таким образом, эквивалентная схема представляет собой источник тока 3,75 мА, подключенный параллельно резистору сопротивлением 2 кОм.

Преобразование в эквивалент Тевенена

Эквивалентная схема Нортона связана с эквивалентом Тевенена уравнениями:

{\begin{aligned}&R_{\rm {th}}=R_{\rm {no}}\\[8pt]&V_{\rm {th}}=I_{\rm {no}}R_{\rm {no}}\\[8pt]&{\frac {V_{\rm {th}}}{R_{\rm {th}}}}=I_{\rm {no}}\end{aligned}}

Теория массового обслуживания

Пассивный схемный эквивалент «теоремы Нортона» в теории массового обслуживания называется теоремой Чанди Херцога Ву . ^{[ 3 ]}^{[ 4 ]}^{[ 7 ]} В обратимой системе массового обслуживания часто можно заменить неинтересное подмножество очередей одной очередью ( FCFS или PS ) с соответствующим образом выбранной скоростью обслуживания. ^{[ 8 ]}

См. также

Ссылки

^ Майер, Ганс Фердинанд (1926). «О эквивалентных схемах электронных усилителей». Телеграфная и телефонная техника (на немецком языке). 15 :335-337.
^ Нортон, Эдвард Лоури (1926). «Проектирование конечных сетей с однородной частотной характеристикой». Лаборатории Белла . Технический отчет TM26–0–1860. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
^ Jump up to: ^а ^б Джонсон, Дон Х. (2003). «Истоки концепции эквивалентной схемы: эквивалент источника напряжения» (PDF) . Труды IEEE . 91 (4): 636–640. дои : 10.1109/JPROC.2003.811716 . HDL : 1911/19968 .
^ Jump up to: ^а ^б Джонсон, Дон Х. (2003). «Истоки концепции эквивалентной схемы: эквивалент источника тока» (PDF) . Труды IEEE . 91 (5): 817–821. дои : 10.1109/JPROC.2003.811795 .
^ Бриттен, Джеймс Э. (март 1990 г.). «Теорема Тевенена» . IEEE-спектр . 27 (3): 42. дои : 10.1109/6.48845 . S2CID 2279777 . Проверено 1 февраля 2013 г.
^ Дорф, Ричард С .; Свобода, Джеймс А. (2010). «Глава 5: Теоремы о цепях» . Введение в электрические цепи (8-е изд.). Хобокен, Нью-Джерси, США: John Wiley & Sons . стр. 162–207. ISBN 978-0-470-52157-1 . Архивировано из оригинала 30 апреля 2012 г. Проверено 8 декабря 2018 г.
^ Гюнтер, Нил Дж. (2004). Анализ производительности компьютерной системы с помощью Perl::PDQ (Интернет-изд.). Берлин: Springer Science + Business Media . п. 281. ИСБН 978-3-540-20865-5 .
^ Чанди, Каниантра-Мани ; Херцог, Ульрих; Ву, Лин С. (январь 1975 г.). «Параметрический анализ сетей массового обслуживания» . Журнал исследований и разработок IBM . 19 (1): 36–42. дои : 10.1147/rd.191.0036 .

Внешние ссылки

СМИ, связанные с теоремой Нортона, на Викискладе?
Теорема Нортона на allaboutcircuits.com

[Mayer_1926-1] Майер, Ганс Фердинанд (1926). «О эквивалентных схемах электронных усилителей». Телеграфная и телефонная техника (на немецком языке). 15 :335-337.

[Norton_1926-2] Нортон, Эдвард Лоури (1926). «Проектирование конечных сетей с однородной частотной характеристикой». Лаборатории Белла . Технический отчет TM26–0–1860. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[Johnson_2003a-3] Jump up to: ^а ^б Джонсон, Дон Х. (2003). «Истоки концепции эквивалентной схемы: эквивалент источника напряжения» (PDF) . Труды IEEE . 91 (4): 636–640. дои : 10.1109/JPROC.2003.811716 . HDL : 1911/19968 .

[Johnson_2003b-4] Jump up to: ^а ^б Джонсон, Дон Х. (2003). «Истоки концепции эквивалентной схемы: эквивалент источника тока» (PDF) . Труды IEEE . 91 (5): 817–821. дои : 10.1109/JPROC.2003.811795 .

[Brittain_1990-5] Бриттен, Джеймс Э. (март 1990 г.). «Теорема Тевенена» . IEEE-спектр . 27 (3): 42. дои : 10.1109/6.48845 . S2CID 2279777 . Проверено 1 февраля 2013 г.

[Dorf_2010-6] Дорф, Ричард С .; Свобода, Джеймс А. (2010). «Глава 5: Теоремы о цепях» . Введение в электрические цепи (8-е изд.). Хобокен, Нью-Джерси, США: John Wiley & Sons . стр. 162–207. ISBN 978-0-470-52157-1 . Архивировано из оригинала 30 апреля 2012 г. Проверено 8 декабря 2018 г.

[Gunther_2004-7] Гюнтер, Нил Дж. (2004). Анализ производительности компьютерной системы с помощью Perl::PDQ (Интернет-изд.). Берлин: Springer Science + Business Media . п. 281. ИСБН 978-3-540-20865-5 .

[Chandy_1975-8] Чанди, Каниантра-Мани ; Херцог, Ульрих; Ву, Лин С. (январь 1975 г.). «Параметрический анализ сетей массового обслуживания» . Журнал исследований и разработок IBM . 19 (1): 36–42. дои : 10.1147/rd.191.0036 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]