Параллельно (оператор)

Параллельный оператор (произносится «параллельно», [1] следуя обозначениям параллельных линий из геометрии ; [2] [3] также известная как приведенная сумма , параллельная сумма или параллельное сложение ) — математическая функция , которая используется как сокращение в электротехнике . [4] [5] [6] [номер 1] но также используется в кинетике , механике жидкостей и финансовой математике . [7] [8] Название «параллельный» происходит от использования оператора, вычисляющего совместное сопротивление резисторов параллельно .
Обзор [ править ]
Параллельный оператор представляет обратное значение суммы обратных значений (иногда также называемое «формулой взаимности» или « гармонической суммой») и определяется следующим образом: [9] [6] [10] [11]
где а , б и являются элементами расширенных комплексных чисел [12] [13]
Оператор дает половину среднего гармонического двух чисел a и b . [7] [8]
В частном случае для любого числа :
Далее, для всех различных чисел :
с представляющее собой ценность абсолютную , и что означает минимум (наименьший элемент) среди x и y .
Если и являются различными положительными действительными числами, тогда
Концепция была расширена со скалярной операции на матрицы. [14] [15] [16] [17] [18] и далее обобщается . [19]
Обозначения [ править ]
Первоначально оператор был представлен как приведенная сумма в 1956 году. Сундарамом Сешу [20] [21] [14] учился на оператора ∗ Кентом Э. Эриксоном в 1959 году, [22] [23] [14] и популяризирован Ричардом Джеймсом Даффином и Уильямом Найлсом Андерсоном-младшим как параллельного сложения или параллельной суммы. оператор : по математике и теории сетей с 1966 года. [15] [16] [1] Хотя некоторые авторы продолжают использовать этот символ до настоящего времени, [7] [8] например, Суджит Кумар Митра использовал ∙ как символ в 1970 году. [14] В прикладной электронике А. ∥ Знак стал более распространенным в качестве символа оператора примерно в 1974 году. [24] [25] [26] [27] [28] [номер 1] [номер 2] Часто это записывалось как двойная вертикальная линия (||), доступная в большинстве наборов символов (иногда выделенная курсивом как //[29] [30] ), но теперь его можно представить с помощью символа Юникода U+2225 ( ∥ ) для «параллельно». В LaTeX и родственных языках разметки макросы \| и \parallel часто (и редко) используются \smallparallel используется) для обозначения символа оператора.
Свойства [ править ]
Позволять представляют собой расширенную комплексную плоскость, исключающую ноль, и биективная функция из к такой, что У одного есть личности
и
Это сразу означает, что — это поле , в котором параллельный оператор заменяет сложение, и что это изоморфно поле
Следующие свойства могут быть получены путем перевода через соответствующие свойства комплексных чисел.
Свойства поля [ править ]
Что касается любой сферы, удовлетворяет множеству базовых тождеств.
Он коммутативен при параллели и умножении:
Ассоциативен относительно параллели и умножения: [12] [7] [8]
Обе операции имеют идентификации элемент ; для параллельного тождество в то время как для умножения тождество равно 1 :
Каждый элемент из имеет обратную относительно параллельности, равную аддитивная обратная по сложению. (Но 0 не имеет обратного значения при параллельности.)
Элемент идентификации является своей собственной инверсией,
Каждый элемент из имеет мультипликативную обратную :
Умножение является распределительным по параллельному: [1] [7] [8]
Повторная параллель [ править ]
Повторная параллель эквивалентна делению,
Или, умножив обе части на n ,
В отличие от повторного сложения , это не коммутирует:
Биномиальное разложение [ править ]
Дважды используя распределительное свойство, произведение двух параллельных биномов можно разложить как
Квадрат бинома равен
Куб бинома - это
В общем, n- я степень бинома может быть расширена с использованием биномиальных коэффициентов , которые являются обратными добавляемым, что приводит к аналогу биномиальной формулы :
Логарифм и экспонента [ править ]
Имеют место следующие тождества:
Параллельные функции [ править ]
— Параллельная функция это функция, которая коммутирует с параллельной операцией: [ нужна ссылка ]
Например, является параллельной функцией, так как
полиномов параллельных Факторизация
Как и сложенный многочлен , параллельный многочлен с коэффициентами в (с ) можно разложить в произведение мономов:
для некоторых корней (возможно, повторяется) в
Аналогично сложению многочленов, полиномиальное уравнение
подразумевает, что для некоторого k .
Квадратичная формула [ править ]
Линейное уравнение можно легко решить с помощью обратного параллельного уравнения:
Чтобы решить параллельное квадратное уравнение, дополните квадрат , чтобы получить аналог квадратной формулы
Включая ноль [ править ]
Расширенные комплексные числа, включая ноль, больше не является полем при параллельном и умножении, поскольку 0 не имеет обратного при параллельном. (Это аналогично тому, как это не поле, потому что не имеет аддитивного обратного.)
Для каждого ненулевого a ,
Количество можно либо оставить неопределенным (см. неопределенную форму ), либо определить равным 0 .
Приоритет [ править ]
При отсутствии круглых скобок параллельный оператор определяется как имеющий приоритет над сложением или вычитанием, аналогично умножению. [1] [31] [9] [10]
Приложения [ править ]
Существуют приложения параллельного оператора в электронике, оптике и изучении периодичности:
цепи [editанализ
В электротехнике параллельный оператор можно использовать для расчета полного сопротивления различных последовательных и параллельных электрических цепей. [номер 2] Существует двойственность между обычной (последовательной) суммой и параллельной суммой. [7] [8]
Например, общее сопротивление резисторов, соединенных параллельно, является обратной суммой обратных величин отдельных резисторов .
Аналогично и для общей емкости последовательных конденсаторов . [номер 2]
линзы Уравнение
В геометрической оптике — приближение тонкой линзы к уравнению производителя линз.
Синодический editпериод
Время между соединениями двух вращающихся тел называется синодическим периодом . Если период более медленного тела равен Т 2 , а период более быстрого - Т 1 , то синодический период равен
Примеры [ править ]
Вопрос:
- Три резистора , и соединены параллельно . Каково их результирующее сопротивление?
Отвечать:
- Эффективно возникающее сопротивление составляет ок. 57 кОм .
- Строитель возводит стену за 5 часов. Другому работнику на ту же работу потребуется 7 часов. Сколько времени потребуется на постройку стены, если оба рабочих работают параллельно?
Отвечать:
- Они закончатся примерно через 3 часа.
Реализация [ править ]

Предложенная еще Кентом Э. Эриксоном в качестве подпрограммы в цифровых компьютерах в 1959 году, [22] параллельный оператор реализован как оператор клавиатуры на научных калькуляторах обратной польской нотации (RPN) WP 34S с 2008 года. [32] [33] [34] так же как и на WP 34C [35] и WP 43S с 2015 г., [36] [37] позволяя решать даже каскадные проблемы с помощью нескольких нажатий клавиш, таких как 270↵ Enter180∥120∥.
Проекционный вид [ править ]
данного поля F существует два вложения F z в проективную прямую P( F ): z → [ Для : 1] и z → [1: z ]. Эти вложения перекрываются, за исключением [0:1] и [1:0]. Параллельный оператор связывает операцию сложения между вложениями. Фактически гомографии на проективной прямой представляются матрицами M(2, F ) размера 2 x 2, а полевые операции (+ и ×) расширяются до гомографий. Каждое вложение имеет дополнение a + b, представленное следующими матричными умножениями в M(2, A ):
Два матричных произведения показывают, что существуют две подгруппы M(2, F изоморфные ( F ,+), аддитивной группе F. ) , В зависимости от того, какое вложение используется, одна операция — +, другая —
Примечания [ править ]
- ↑ Перейти обратно: Перейти обратно: а б Хотя символ ∥, обозначающий «параллель», в геометрии появился еще в 1673 году в работе Джона Керси-старшего , [А] это стало более широко использоваться только примерно с 1875 года. [Б] Использование математического оператора для параллельных цепей берет свое начало из теории сетей в электротехнике . Сундарам Сешу представил оператор приведенной суммы в 1956 году: [С] Кент Э. Эриксон предложил звездочку (∗) для обозначения оператора в 1959 году: [Д] в то время как Ричард Джеймс Даффин и Уильям Найлз Андерсон-младший использовали двоеточие (:) для параллельного сложения с 1966 года. [И] Суджит Кумар Митра использовал для этого среднюю точку (∙) в 1970 году. [Ф] Первое использование параллельного символа (∥) для этого оператора в прикладной электронике неизвестно, но, возможно, оно произошло из книги Стивена Д. Сентурии и Брюса Д. Уэдлока 1974 года «Электронные схемы и приложения». [Г] которые развились из их вводного курса электроники в Массачусетском технологическом институте (MIT) с концепциями преподавания теории сетей и электроники, заимствованными из более раннего курса, который вел Кэмпбелл «Кэм» Лич Сирл . Дальнейшую популяризацию он получил благодаря книге Джона В. Маквейна 1981 года «Введение в электронику и приборостроение». [ЧАС] Этот символ , вероятно, был также введен потому , что другие используемые символы можно было легко спутать со знаками, обычно используемыми для умножения и деления в некоторых контексты.
- ↑ Перейти обратно: Перейти обратно: а б с В электрических цепях оператор параллельности может применяться соответственно к параллельным сопротивлениям ( R в [Ом]) или индуктивностям ( L в [Гн]), а также к импедансам ( Z в [Ом]) или реактивным сопротивлениям ( X в [Ом] ]). символа оператора, Игнорируя вводящий в заблуждение символ его также можно применять к последовательным цепям соответственно с проводимостями ( G в [S]) или емкостями ( C в [F]), а также к проводимостям ( Y в [S]) или проводимости ( B в [S]).
Ссылки [ править ]
- ↑ Перейти обратно: Перейти обратно: а б с д Даффин, Ричард Джеймс (1971) [1970, 1969]. «Сетевые модели» . Написано в Дареме, Северная Каролина, США. В Уилфе, Герберт Саул ; Харарей, Фрэнк (ред.). Математические аспекты анализа электрических сетей . Материалы симпозиума по прикладной математике Американского математического общества и Общества промышленной и прикладной математики, состоявшегося в Нью-Йорке, 03 февраля 1969 г. Том. III из SIAM-AMS Proceedings (иллюстрированное издание). Провиденс, Род-Айленд: Американское математическое общество (AMS) / Общество промышленной и прикладной математики (SIAM). С. 65–92 [68]. ISBN 0-8218-1322-6 . ISSN 0080-5084 . LCCN 79-167683 . ISBN 978-0-8218-1322-5 . Отчет 69-21 . Проверено 5 августа 2019 г. С. 68–69:
[…] Чтобы иметь удобное краткое обозначение совместного сопротивления резисторов, соединенных параллельно, пусть […] A:B = AB/(A+B) […] A:B можно рассматривать как новая операция, называемая параллельным сложением […] Параллельное сложение определено для любых неотрицательных чисел. Сетевая модель показывает, что параллельное сложение коммутативно и ассоциативно . Более того, умножение является распределительным по этой операции. Рассмотрим теперь алгебраическое выражение в операциях (+) и (:), действующее на положительные числа A, B, C и т. д. […] Чтобы дать сетевую интерпретацию такого полинома, прочтите A + B как «серия A B» и A : B как «Параллель B», тогда ясно, что выражение […] представляет собой совместное сопротивление сети […]
[1] [2] (206 страниц) - ^ Керси (старший), Джон (1673). «Глава I: О сфере применения этой четвертой книги и значении используемых в ней символов, сокращений и цитат». Элементы того математического искусства, которое обычно называют алгеброй . Том. Книга IV - Элементы алгебраических искусств. Лондон: Томас Пассинджер, Три Библии, Лондон-Бридж. стр. 177–178. Архивировано из оригинала 5 августа 2020 г. Проверено 9 августа 2019 г.
- ^ Каджори, Флориан (1993) [сентябрь 1928 г.]. «§ 184, § 359, § 368». История математических обозначений - Обозначения в элементарной математике . Том. 1 (два тома в одном неизмененном переиздании). Чикаго, США: Издательская компания открытого суда . стр. 193, 402–403, 411–412 . ISBN 0-486-67766-4 . LCCN 93-29211 . Проверено 22 июля 2019 г. стр. 402–403, 411–412:
§359. […] ∥ параллель встречается в Отреда Opuscula mathematica hactenus inedita (1677) [стр. 197], посмертное произведение (§ 184) […] §368. Знаки параллельных линий. […] когда знак равенства Рекорда завоевал распространение на континенте , вертикальные линии стали использоваться для параллельности. Мы находим ∥ для «параллельного» в Керси , [А] Касвелл , Джонс , [Б] Уилсон, [С] Эмерсон , [Д] Камбли, [И] и писатели последних пятидесяти лет, которых уже цитировали в связи с другими пиктограммами. Примерно до 1875 года это происходило не так часто […] Холл и Стивенс. [Ф] используйте «пар. [Ф] или ∥» для параллельного […] [A] Джон Керси , Алгебра (Лондон, 1673), Книга IV, стр. 177. [B] У. Джонс , Synopsis palmarioum matheseos (Лондон, 1706). [C] Джон Уилсон, Тригонометрия (Эдинбург, 1714 г.), объяснение персонажей [D] W. Emerson , Elements of Geometry (Лондон, 1763), стр. 4. [E] L. Kambly , Die Elementar-Mathematik , Part 2: Planimetrie , 43. издание (Бреслау, 1876 г.), стр. 8. […] [F] Х. С. Холл и Ф. Х. Стивенс, «Элементы Евклида» , части I и II (Лондон, 1889 г.), стр. 10. […]
[3] - ^ «INA 326/INA 327 — прецизионный инструментальный усилитель ввода-вывода с Rail-to-Rail» (PDF) . Берр-Браун / Texas Instruments . 2018 [ноябрь 2004 г., ноябрь 2001 г.]. С. 3, 9, 13. СБОС222Д. Архивировано (PDF) из оригинала 13 июля 2019 г. Проверено 13 июля 2019 г.
- ^ Бобер, Уильям; Стивенс, Эндрю (2016). «Глава 7.6. Преобразования Лапласа, применяемые к схемам» . Численные и аналитические методы с MATLAB для инженеров-электриков . Прикладная и вычислительная механика (1-е изд.). ЦРК Пресс . п. 224. ИСБН 978-1-46657607-0 . ISBN 1-46657607-3 . (388 страниц)
- ↑ Перейти обратно: Перейти обратно: а б Ранаде, Гирея; Стоянович, Владимир, ред. (осень 2018 г.). «Глава 15.7.2 Параллельные резисторы» (PDF) . EECS 16A Проектирование информационных устройств и систем I (PDF) (конспекты лекций). Калифорнийский университет в Беркли . п. 12. Примечание 15. Архивировано (PDF) из оригинала 27 декабря 2018 г. Проверено 28 декабря 2018 г. п. 12:
[…] Это математическое соотношение встречается достаточно часто, поэтому у него даже есть название: «параллельный оператор», обозначаемый ∥. Когда мы говорим x∥y, это означает . Обратите внимание, что это математический оператор, который ничего не говорит о фактической конфигурации. В случае с резисторами для параллельных резисторов используется оператор параллельности, но для других компонентов (например, конденсаторов) это не так. […]
(16 страниц) - ↑ Перейти обратно: Перейти обратно: а б с д и ж г Эллерман, Дэвид Паттерсон (21 марта 1995 г.). «Глава 12: Параллельное сложение, последовательно-параллельная двойственность и финансовая математика» . Интеллектуальное посягательство как образ жизни: очерки философии, экономики и математики (PDF) . Мирская философия: исследования на стыке философии и экономики (иллюстрированное изд.). Rowman & Littlefield Publishers, Inc., стр. 237–268. ISBN 0-8476-7932-2 . Архивировано (PDF) из оригинала 5 марта 2016 г. Проверено 9 августа 2019 г. п. 237:
[…] Когда резисторы с сопротивлением a и b соединены последовательно, их составное сопротивление представляет собой обычную сумму (далее последовательная сумма ) сопротивлений a + b. Если сопротивления расположены параллельно, их составное сопротивление представляет собой параллельную сумму сопротивлений, которая обозначается полным двоеточием […]
[4] (271 страница) - ↑ Перейти обратно: Перейти обратно: а б с д и ж г Эллерман, Дэвид Паттерсон (май 2004 г.) [21 марта 1995 г.]. «Введение в последовательно-параллельную двойственность» (PDF) . Калифорнийский университет в Риверсайде . CiteSeerX 10.1.1.90.3666 . Архивировано из оригинала 10 августа 2019 г. Проверено 9 августа 2019 г.
Параллельная сумма двух положительных действительных чисел x:y = [(1/x) + (1/y)] −1 возникает в теории электрических цепей как сопротивление, возникающее в результате параллельного соединения двух сопротивлений x и y. Существует двойственность между обычной (последовательной) суммой и параллельной суммой. […]
[5] (24 страницы) - ↑ Перейти обратно: Перейти обратно: а б Бассо, Кристоф П. (2016). «Глава 1.1.2 Делитель тока» . Передаточные функции линейной схемы: введение в быстрые аналитические методы (1-е изд.). Чичестер, Западный Суссекс, Нью-Джерси, США: John Wiley & Sons Ltd., с. 12. ISBN 978-1-11923637-5 . LCCN 2015047967 . Проверено 28 декабря 2018 г. (464 страницы)
- ↑ Перейти обратно: Перейти обратно: а б Коттер, Нил Э., изд. (12 октября 2015 г.) [20 сентября 2014 г.]. «Поваренная книга ECE1250 – Узлы, серии, параллельность» (конспекты лекций). Кулинарные книги. Университет Юты . Архивировано (PDF) из оригинала 20 августа 2020 г. Проверено 11 августа 2019 г.
[…] Один из удобных способов указать, что два резистора включены параллельно, — поставить между ними знак ∥. […]
- ^ Бёккер, Иоахим (18 марта 2019 г.) [апрель 2008 г.]. «Основы электротехники, часть B» (PDF) (на немецком языке). Университет Падерборна . п. 12. Архивировано (PDF) из оригинала 17 апреля 2018 г. Проверено 9 августа 2019 г. п. 12:
Для расчета эквивалентного сопротивления параллельного соединения […] часто используется краткое обозначение ∥.
- ↑ Перейти обратно: Перейти обратно: а б Георг, Отфрид (2013) [1999]. «Глава 2.11.4.3: Определение дифференциального уравнения из комплексного представления — Приложение MATHCAD 2.11-6: Пользовательские операторы» . Электромагнитные поля и сети: приложения в Mathcad и PSpice . Учебник Springer (на немецком языке) (1-е изд.). Издательство Спрингер . стр. 246–248. дои : 10.1007/978-3-642-58420-6 . ISBN 978-3-642-58420-6 . ISBN 3-642-58420-9 . Проверено 4 августа 2019 г. (728 страниц)
- ^
 Ассоциативная композиционная алгебра/гомографии в Wikibooks
Ассоциативная композиционная алгебра/гомографии в Wikibooks - ↑ Перейти обратно: Перейти обратно: а б с д Митра, Суджит Кумар (февраль 1970 г.). «Матричная операция для анализа последовательно-параллельных многопортовых устройств» . Журнал Института Франклина . Краткое сообщение. 289 (2). Институт Франклина : 167–169. дои : 10.1016/0016-0032(70)90302-9 . п. 167:
Целью данного сообщения является распространение концепции скалярной операции «Приведенная сумма», введенной Сешу […] и позже разработанной Эриксоном […], на матрицы, обрисовывание некоторых интересных свойств этой новой матричной операции и применение матричные операции при анализе последовательных и параллельных n -портовых сетей . Пусть A и B — две невырожденные квадратные матрицы, имеющие обратные , A −1 и Б −1 соответственно. Определим операцию ∙ как A ∙ B = (A −1 + Б −1 ) −1 и операцию ⊙ как A ⊙ B = A ∙ (−B). Операция ∙ коммутативна и ассоциативна , а также дистрибутивна относительно умножения. […]
(3 страницы) - ↑ Перейти обратно: Перейти обратно: а б Даффин, Ричард Джеймс ; Хазони, Дов; Моррисон, Норман Александр (март 1966 г.) [12 апреля 1965 г., 25 августа 1964 г.]. «Сетевой синтез с помощью гибридных матриц». SIAM Journal по прикладной математике . 14 (2). Общество промышленной и прикладной математики (SIAM): 390–413. дои : 10.1137/0114032 . JSTOR 2946272 . (24 страницы)
- ↑ Перейти обратно: Перейти обратно: а б Андерсон-младший, Уильям Найлз; Даффин, Ричард Джеймс (1969) [1968-05-27]. «Последовательное и параллельное сложение матриц» . Журнал математического анализа и приложений . 26 (3). Academic Press, Inc .: 576–594. дои : 10.1016/0022-247X(69)90200-5 . п. 576:
[…] параллельную сумму A и B определяем по формуле A(A + B) + B и обозначим его через A : B. Если A и B неособые, это сводится к A : B = (A −1 + Б −1 ) −1 это хорошо известная электрическая формула для параллельного соединения резисторов. Затем показано, что эрмитовы полуопределенные матрицы образуют коммутативную частично упорядоченную полугруппу при выполнении параллельной операции суммирования. […]
[6] - ^ Митра, Суджит Кумар; Пури, Мадан Лал (октябрь 1973 г.). «О параллельной сумме и разности матриц» (PDF) . Журнал математического анализа и приложений . 44 (1). Academic Press, Inc .: 92–97. дои : 10.1016/0022-247X(73)90027-9 . Архивировано из оригинала (PDF) 13 апреля 2019 г.
- ^ Митра, Суджит Кумар; Бхимасанкарам, Почираджу; Малик, Сарой Б. (2010). Матричные частичные заказы, сокращенные операторы и приложения . Серия по алгебре. Том. 10 (иллюстрировано 1-м изд.). World Scientific Publishing Co. Pte. ООО ISBN 978-981-283-844-5 . ISBN 981-283-844-9 . Проверено 19 августа 2019 г. (446 страниц)
- ^ Эрикссон-Бике, Сиркка-Лиза Аннели [на финском языке] ; Лейтвилер, Хайнц (февраль 1989 г.) [10 января 1989]. «Обобщение параллельного сложения» (PDF ) уравнения Математические 38 (1). Издательство Биркхойзер : 99–110. дои : 10.1007/BF01839498 . Архивировано (PDF) из оригинала 2 августа 2020 г. Получено 2 августа 2020 г.
- ^ Сешу, Сундарам (сентябрь 1956 г.). «Об электрических цепях и коммутационных схемах» . IRE Транзакции по теории цепей . КТ-3 (3). Институт радиоинженеров (ИРЭ): 172–178. дои : 10.1109/TCT.1956.1086310 . (7 страниц) (Примечание. См. исправления .)
- ^ Сешу, Сундарам; Гулд, Родерик (сентябрь 1957 г.). «Поправка к «Об электрических цепях и цепях коммутации» » . IRE Транзакции по теории цепей . Исправление. КТ-4 (3). Институт радиоинженеров (ИРЭ): 284. doi : 10.1109/TCT.1957.1086390 . (1 страница) (Примечание. Относится к предыдущей ссылке.)
- ↑ Перейти обратно: Перейти обратно: а б Эриксон, Кент Э. (март 1959 г.). «Новая операция анализа последовательно-параллельных сетей» . IRE Транзакции по теории цепей . КТ-6 (1). Институт радиоинженеров (ИРЭ): 124–126. дои : 10.1109/TCT.1959.1086519 . п. 124:
[…] Операция ∗ определяется как A ∗ B = AB/A + B. Символ ∗ обладает алгебраическими свойствами, которые упрощают формальное решение многих последовательно-параллельных сетевых задач. Если бы операцию ∗ включить в качестве подпрограммы в цифровой компьютер , это могло бы упростить программирование некоторых сетевых вычислений. […]
(3 страницы) (Примечание. См. комментарий .) - ^ Кауфман, Ховард (июнь 1963 г.). «Замечание о новой операции анализа последовательно-параллельных сетей». Транзакции IEEE по теории цепей . КТ-10 (2). Институт инженеров по электротехнике и электронике (IEEE): 283. doi : 10.1109/TCT.1963.1082126 . п. 283:
[…] Комментарии к операции ∗ […] a∗b = ab/(a+b) […]
(1 страница) (Примечание. Относится к предыдущей ссылке.) - ^ Сентурия, Стивен Д. [в Викиданных] ; Уэдлок, Брюс Д. (1975) [август 1974 г.]. «Часть А. Изучение языка, Глава 3. Линейные резистивные сети, 3.2 Базовые конфигурации сетей, 3.2.3. Резисторы параллельно». Написано в Массачусетском технологическом институте, Кембридж, Массачусетс, США. Электронные схемы и приложения (1-е изд.). Нью-Йорк, Лондон, Сидней, Торонто: John Wiley & Sons, Inc., стр. viii–ix, 44–46 [45]. ISBN 0-471-77630-0 . LCCN 74-7404 . S2CID 61070327 . стр. viii, ix, 45:
Этот учебник создан на основе односеместрового вводного курса по электронике, преподаваемого авторами в Массачусетском технологическом институте . […] Этот курс используется многими первокурсниками в качестве предшественника основной программы MIT по электротехнике. […] В подготовке книги такого размера приняли участие многие люди. Концепция преподавания теории сетей и электроники как единого предмета заимствована у профессора Кэмпбелла Сирла , который преподавал вводный курс электроники, когда один из нас ( SDS ) был аспирантом первого курса физики и пытался изучать электронику. Кроме того, профессор Сирл предоставил неоценимую конструктивную критику на протяжении всего написания этого текста. Несколько преподавателей Массачусетского технологического института и около 40 технических ассистентов приняли участие в преподавании этого материала за последние пять лет, многие из которых внесли важный вклад своими предложениями и примерами. Среди них мы особенно хотим поблагодарить О. Р. Митчелла, Ирвина Ингландера, Джорджа Льюиса, Эрнеста Винсента, Дэвида Джеймса, Кенуэя Вонга, Гима Хома, Тома Дэвиса, Джеймса Киртли и Роберта Донахи. Председатель кафедры электротехники MIT, профессор Луис Д. Смуллин , как и многие коллеги по всему отделу, оказывал поддержку и поддержку в ходе этого проекта. […] Первый результат […] гласит, что общее напряжение на параллельной комбинации R 1 и R 2 такое же, как и на одном сопротивлении номиналом R 1 R 2 (R 1 + R 2 ). Поскольку это выражение для параллельного сопротивления встречается очень часто, ему присвоено специальное обозначение (R 1 ∥R 2 ). То есть, когда R1 и R2 включены параллельно, эквивалентное сопротивление равно […]
(xii+623+5 страниц) (Примечание. Также было доступно пособие для учителя. Ранние тиражи содержат значительное количество опечаток. См. также: книга Уэдлока 1978 года .) [7] - ^ Вольф, Лоуренс Дж. (1977) [1976, 1974]. «Раздел 4. Учебные материалы - 4.3. Проект разработки технической учебной программы MIT - Введение в электронику и приборостроение». В Олдридже, Билл Г.; Мауэри, Дональд Р.; Вольф, Лоуренс Дж.; Диксон, Пегги (ред.). Наука и инженерные технологии – Руководство по учебной программе: Руководство по двухлетней учебной программе для получения степени младшего специалиста (PDF) . Общественный колледж Сент-Луиса – Флориссан-Вэлли , Сент-Луис, Миссури, США: Национальная ассоциация преподавателей естественных наук , Вашингтон, округ Колумбия, США. стр. 21, 77. Архивировано (PDF) из оригинала 15 февраля 2017 г. Проверено 8 августа 2019 г. п. 21:
[…] «Введение в электронику и приборостроение » — это новый и современный подход к вводному курсу электроники. Предназначенный для студентов, не имеющих опыта работы с электроникой, он развивает навыки и знания, необходимые для использования и понимания современных электронных систем. […] Джон В. МакВейн […]
(Примечание. Проект SET представлял собой двухлетнюю учебную программу для выпускников средней школы, разработанную между 1974 и 1977 годами для подготовки технических специалистов для использования электронных инструментов.) - ^ Визнер, Джером Берт ; Джонсон, Ховард Уэсли ; Киллиан-младший, Джеймс Райн , ред. (11 апреля 1978 г.). «Инженерная школа - Центр перспективных инженерных исследований (CAES) - Исследования и разработки - Проект исследований и разработок технической учебной программы». Отчет президента и канцлера за 1977–78 годы - Массачусетский технологический институт (PDF) . Массачусетский технологический институт (MIT). стр. 249, 252–253. Архивировано (PDF) из оригинала 10 сентября 2015 г. Проверено 8 августа 2019 г. . 249, 252–253:
[…] Программа исследований и разработок технической учебной программы, спонсируемая Имперской организацией социальных служб Ирана стр , вступает в четвертый год пятилетнего контракта. Продолжается разработка учебных программ по электронике и машиностроению. […] Проект, управляемый совместно CAES и Департаментом материаловедения и инженерии , находится под руководством профессора Мертона К. Флемингса. Режиссер - доктор Джон В. МакВейн. […] Разработка учебных материалов. Это основная деятельность проекта, направленная на разработку инновационных, современных учебных материалов в необходимых областях инженерных технологий […] новый вводный курс по электронике […] называется «Введение в электронику и приборостроение». и состоит из восьми […] модулей […] постоянного тока, напряжения и сопротивления; Базовые сети; Изменяющиеся во времени сигналы; Операционные усилители; Источники питания; переменный ток, напряжение и сопротивление; цифровые схемы; и электронные измерения и контроль. Этот курс представляет собой серьезное изменение и обновление способа внедрения электроники и должен иметь большую ценность для STI, а также ко многим программам США. […]
- ^ Уэдлок, Брюс Д. (1978). Основные схемы сетей . Введение в электронику и приборостроение. Массачусетский технологический институт (MIT), Проект исследований и разработок технической учебной программы. (81 страница) (Примечание. Это легло в основу первой части книги Сентурии и Уэдлока 1975 года МакВейна 1981 года. См. Также: книгу .)
- ^ МакВейн, Джон В. (1 мая 1981 г.). Введение в электронику и приборостроение (иллюстрированное изд.). Норт-Ситуэйт, Массачусетс, США: Breton Publishers , Wadsworth, Inc., стр. 78, 96–98, 100, 104. ISBN 0-53400938-7 . ISBN 978-0-53400938-0 . Проверено 4 августа 2019 г. п. xiii, 96–98, 100:
[…] Брюс Д. Уэдлок […] был основным автором части I, БАЗОВЫЕ СХЕМЫ СЕТИ, включая разработку сопутствующих примеров. […] Большая часть разработки программы IEI была предпринята в рамках проекта исследований и разработок технической учебной программы Центра перспективных инженерных исследований Массачусетского технологического института . […] Сокращенное обозначение […] Сокращенный символ ∥ […]
(xiii+545 страниц) (Примечание. В 1981 году также существовало 216-страничное лабораторное руководство, сопровождающее эту книгу. Работа выросла из Массачусетского технологического института программы курса « The Проект разработки технической учебной программы MIT «Введение в электронику и приборостроение » разрабатывался между 1974 и 1979 годами. В 1986 году вышло второе издание этой книги под названием «Введение в электронные технологии».) - ^ «7.5.3 Выбор внешнего сопротивления». TPL5110 Системный таймер Nano-Power для управления питанием (PDF) (техническое описание). Редакция А. Texas Instruments Incorporated . Сентябрь 2018 г. [январь 2015 г.]. стр. 13–14. СНАС650А. Архивировано (PDF) из оригинала 25 сентября 2022 г. Проверено 25 сентября 2022 г. (27 страниц)
- ^ «A7987: Асинхронный понижающий импульсный стабилизатор с регулируемым ограничением тока для автомобилей, 61 В, 3 А» (PDF) (техническое описание). Редакция 3. STMicroelectronics NV . 22 сентября 2020 г. [19 марта 2019 г.]. стр. 17, 18, 20. DS12928. Архивировано (PDF) из оригинала 18 июля 2022 г. Проверено 18 июля 2022 г. (36 страниц)
- ^ Пол, Штеффен; Пол, Рейнхольд (24 октября 2014 г.). «Глава 2.3.2: Соединения линейно-резистивного двухполюсного – параллельного соединения» . Основы электротехники и электроники 1: Сети постоянного тока и их применение (на немецком языке). Том 1 (5-е изд.). Издательство Спрингер . п. 78. ИСБН 978-3-64253948-0 . ISBN 3-64253948-3 . Проверено 4 августа 2019 г. п. 78:
[…] При написании сокращенно обращайте особое внимание на использование круглых скобок. […] Знак параллели ∥ в сокращенной записи имеет то же значение, что и знак умножения. Поэтому скобки можно опустить.
(446 страниц) - ^ Дейл, Пол; Бонин, Уолтер (30 ноября 2012 г.) [09 декабря 2008 г.]. Руководство пользователя WP 34S (PDF) (изд. 3.1). стр. 1, 14, 32, 66, 116. Архивировано (PDF) из оригинала 9 июля 2019 г. Проверено 13 июля 2019 г. [8] (211 страниц)
- ^ Бонин, Уолтер (2015) [2008-12-09]. Руководство пользователя WP 34S (изд. 3.3). Независимая издательская платформа CreateSpace . ISBN 978-1-5078-9107-0 . [9]
- ^ Бонин, Уолтер (11 июля 2016 г.) [09 декабря 2008 г.]. Руководство пользователя WP 34S (4-е изд.). Независимая издательская платформа CreateSpace . ISBN 978-1-53366238-5 . ISBN 1-53366238-X . (410 страниц)
- ^ Даурик, Найджел (03 мая 2015 г.) [16 марта 2015 г.]. «Режим сложной блокировки для WP-34» . Музей HP . Архивировано из оригинала 3 апреля 2019 г. Проверено 7 августа 2019 г.
- ^ Бонин, Уолтер (2020) [2015]. Руководство пользователя WP 43S (PDF) . 0,16 (проект ред.). п. 119. ИСБН 978-1-72950098-9 . ISBN 1-72950098-6 . Архивировано (PDF) из оригинала 21 июля 2022 г. Проверено 20 августа 2020 г. [10] [11] (328 страниц)
- ^ Бонин, Уолтер (2020) [2015]. Справочное руководство WP 43S (PDF) . 0,16 (проект ред.). п. 127. ИСБН 978-1-72950106-1 . ISBN 1-72950106-0 . Архивировано (PDF) из оригинала 21 июля 2022 г. Проверено 20 августа 2020 г. [12] [13] (315 страниц)
Дальнейшее чтение [ править ]
- Пекарев, Эдвард Л.; Шмульян, Ю. Л. (30 апреля 1976 г.). «Параллельное сложение и параллельное вычитание операторов» . Математика СССР-Известия . 10 (2). Американское математическое общество : 351–370. Бибкод : 1976ИзМат..10..351П . дои : 10.1070/IM1976v010n02ABEH001694 .
- Даффин, Ричард Джеймс ; Морли, Том Д. (июль 1978 г.). «Почти определенные операторы и электромеханические системы». SIAM Journal по прикладной математике . 35 (1). Общество промышленной и прикладной математики (SIAM): 21–30. дои : 10.1137/0135003 . JSTOR 2101028 . (10 страниц)
- Морли, Том Д. (июль 1979 г.). «Параллельное суммирование, принцип Максвелла и нижняя грань проекций» (PDF) . Журнал математического анализа и приложений . 70 (1). Департамент математики Иллинойского университета в Урбана-Шампейн , Урбана, Иллинойс, США: 33–41. дои : 10.1016/0022-247X(79)90073-8 . Архивировано из оригинала 20 августа 2020 г. Проверено 20 августа 2020 г.
- Сигер, Альберто (май 1990 г.) [1988-03-22]. «Прямое и обратное сложение в выпуклом анализе и приложениях» (PDF) . Журнал математического анализа и приложений . 148 (2). Департамент математики Вашингтонского университета , Сиэтл, Вашингтон, США: Academic Press, Inc .: 317–349. дои : 10.1016/0022-247X(90)90004-Y . Архивировано (PDF) из оригинала 20 августа 2020 г. Проверено 20 августа 2020 г. (33 страницы)
- Брайант, Рэндал Э .; Тайгар, Дж. Дуг; Хуанг, Лоуренс П. (1994). «Геометрическая характеристика последовательно-параллельных сетей переменных резисторов» (PDF) . Транзакции IEEE в схемах и системах I: Фундаментальная теория и приложения . 41 (11): 686–698. дои : 10.1109/81.331520 . Архивировано из оригинала (PDF) 14 августа 2017 г.
- Антезана, Джордж; Корах, Гюстав; Стоянов, Деметриус (апрель 2006 г.) [14 сентября 2005 г.]. «Двусторонние сокращенные операторы и параллельные суммы» (PDF) . Линейная алгебра и ее приложения 414 (2–3). Ла-Плата, Аргентина и Буэнос-Айрес, Аргентина: 570–5. arXiv : math/0509327 . дои : 10.1016/j.laa.2005.10.039 . Архивировано (PDF) из оригинала 0 августа 2017 г. Получено 2 августа 2020 г. [14] (19 страниц)
- Чансангиам, Паттравут (февраль 2016 г.) [август 2015 г., июль 2015 г.]. «Математические аспекты соединений электрических сетей» . Инженерный журнал ККУ . 43 (1): 47–54. дои : 10.14456/kkuenj.2016.8 . Архивировано (PDF) из оригинала 20 августа 2020 г. Проверено 20 августа 2020 г.
- Бесеньей, Адам (01 сентября 2016 г.). «Непреодолимое неравенство Милна» (PDF) . Будапешт: Департамент прикладного анализа и вычислительной математики, Университет Этвеша Лоранда . ЦРУ2016. Архивировано (PDF) из оригинала 8 августа 2019 г. Проверено 11 августа 2019 г.
- «7.5 Электрические характеристики: VCC = 5 В / 7.6 Электрические характеристики: VCC = 2,7 В / 9.1.2.1 Инвертирующий компаратор с гистерезисом». TLV3201, TLV3202: TLV320x 40 нс, microPOWER, двухтактные выходные компараторы (PDF) . Редакция Б. Даллас, Техас, США: Texas Instruments Incorporated . 3 июня 2022 г. [2016, 2012]. С. 5, 6, 13–14 [13]. СБОС561Б. Архивировано (PDF) из оригинала 17 августа 2022 г. Проверено 18 августа 2022 г. п. 5:
ПАРАМЕТР […] ТИП […] ЕДИНИЦА […] ВХОДНОЕ СОПРОТИВЛЕНИЕ […] Общий режим […] 10 13 ∥ 2 […] Ω ∥ пФ […] Дифференциал […] 10 13 ∥ 4 […] Ω ∥ пФ […]
(37 страниц) (Примечание. Необычное использование ∥ как для значений, так и для единиц измерения.)























![{\displaystyle {\begin{aligned}a\parallel b&=b\parallel a\\[3mu]ab&=ba\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33fdcf548e5e335be871903cc2d0cc02147439db)













![{\displaystyle {\begin{aligned}(a\parallel b)(c\parallel d)&=a(c\parallel d)\parallel b(c\parallel d)\\[3mu]&=ac\parallel ad \parallel bc\parallel bd.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75796fff00982215ddf28125ac13967f56303ac6)
![{\displaystyle {\begin{aligned}(a\parallel b)^{2}&=a^{2}\parallel ab\parallel ba\parallel b^{2}\\[3mu]&=a^{2 }\parallel {\tfrac {1}{2}}ab\parallel b^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cc365e2090c31a9a827d434b9def70074105726)















![{\displaystyle {\begin{aligned}ax\parallel b&=\infty \\[3mu]\подразумевает x&=-{\frac {b}{a}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f17b63944689d920e5fe583a2faa06bad488bc9)
![{\displaystyle {\begin{aligned}ax^{2}\parallel bx\parallel c&=\infty \\[5mu]x^{2}\parallel {\frac {b}{a}}x&=-{\ frac {c}{a}}\\[5mu]x^{2}\parallel {\frac {b}{a}}x\parallel {\frac {4b^{2}}{a^{2}} }&=\left(-{\frac {c}{a}}\right)\parallel {\frac {4b^{2}}{a^{2}}}\\[5mu]\left(x\ параллельный {\frac {2b}{a}}\right)^{2}&={\frac {b^{2}\parallel -{\tfrac {1}{4}}ac}{{\tfrac {1 }{4}}a^{2}}}\\[5mu]\подразумевает x&={\frac {(-b)\parallel \pm {\sqrt {b^{2}\parallel -{\tfrac {1 }{4}}ac}}}{{\tfrac {1}{2}}a}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499ed1736b0e0cf7cea1e6de3291ffaacb848cfe)




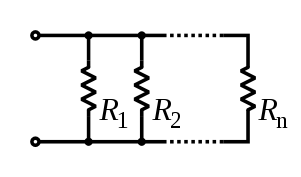
![{\displaystyle {\begin{aligned}{\frac {1}{R_{\text{eq}}}}&={\frac {1}{R_{1}}}+{\frac {1}{R_ {2}}}+\cdots +{\frac {1}{R_{n}}}\\[5mu]R_{\text{eq}}&=R_{1}\parallel R_{2}\parallel \ cdots \parallel R_{n}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92fddb4b991c03b156b12dd85c3cca8c3a3f66c1)





![{\displaystyle {\begin{aligned}R_{1}\parallel R_{2}\parallel R_{3}&=270\,\mathrm {k\Omega } \parallel 180\,\mathrm {k\Omega } \ параллель 120\,\mathrm {k\Omega } \\[5mu]&={\frac {1}{{\dfrac {1}{270\,\mathrm {k\Omega } }}+{\dfrac {1 }{180\,\mathrm {k\Omega } }}+{\dfrac {1}{120\,\mathrm {k\Omega } }}}}\\[5mu]&\approx 56,84\,\mathrm { k\Омега } \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8635ca3fd9bb42d8a264124fe968db472bb0486d)

![{\displaystyle {\begin{aligned}{\begin{pmatrix}1&0\\a&1\end{pmatrix}}{\begin{pmatrix}1&0\\b&1\end{pmatrix}}&={\begin{pmatrix}1&0 \\a+b&1\end{pmatrix}},\\[10mu]{\begin{pmatrix}1&a\\0&1\end{pmatrix}}{\begin{pmatrix}1&b\\0&1\end{pmatrix}}& = {\begin{pmatrix}1&a+b\\0&1\end{pmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a775bf62a63081caef53f3f33667ce290bbc4f5)


