Узор АБАКАБА

Шаблон ABACABA — это рекурсивный фрактальный шаблон , который проявляется во многих местах реального мира (например, в геометрии, искусстве, музыке, поэзии, системах счисления , литературе и высших измерениях ). [1] [2] [3] [4] Шаблоны часто содержат подмножество типа D ABACABA. AA , ABB Также A и AB AA BA . рассматриваются формы типов [5]
Создание шаблона
[ редактировать ]Чтобы сгенерировать следующую последовательность, сначала возьмите предыдущий шаблон, добавьте следующую букву алфавита, а затем повторите предыдущий шаблон. Здесь перечислены первые несколько шагов. [4]
| Шаг | Шаблон | Письма |
|---|---|---|
| 1 | А | 2 1 − 1 = 1 |
| 2 | А Б А | 3 |
| 3 | АБА С АБА | 7 |
| 4 | КВАРТИРА Д- КВАРТИРА | 15 |
| 5 | Льсти E Льсти | 31 |
| 6 | АБАКАБАДАБАКАБАЕАБАКАБАДАБАКАБА Ф АБАКАБАДАБАКАБАААБАКАБАДАБАКАБА | 63 |
АБАКАБА — «быстро растущее слово», часто описываемое как хиастическое или «симметрично организованное вокруг центральной оси» (см.: Хиастическая структура и Χ ). [4] Количество членов в каждой итерации равно a ( n ) = 2 н − 1 , числа Мерсенна ( OEIS : A000225 ).
Галерея
[ редактировать ]- Уровни метрик: [1]Э АБАБАБАБАБАБАБА
- Лестница, построенная из максимально возможных квадратов/кубов, но допускающая ступеньки одинакового размера:КВАРТИРА Д- КВАРТИРА [1]
- Двоично-отраженный код Грея (BRGC):в G
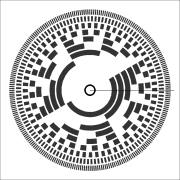
- Поворотный энкодер :мне
- 3-битный код Грея, визуализируемый как обход вершин куба (0,1,3,2,6,7,5,4): [1]АБА С АБА
- Замок Шамбор :АБА С АБА [6]
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Сила, акцент или важность начала каждой продолжительности. длина одного такта в 4
4 (восьмые ноты) разделительно ( , , ), определяемый позицией каждой восьмой ноты в структуре D ABACABA, в то время как восьмые ноты двух тактов группируются аддитивно ( ), определяются структурой E ABACABADABACABA. [3]
Ссылки
[ редактировать ]- ^ Перейти обратно: а б с д и ж г час я дж к л м Нейлор, Майк (февраль 2013 г.). «АБАКАБА Удивительный узор, удивительные связи» . Математические горизонты . Проверено 13 июня 2019 г.
- ^ Перейти обратно: а б с д ШериОЗ (21 апреля 2016 г.). «Изучение фракталов с помощью ABACABA» . Чикагский компьютерщик . Архивировано из оригинала 22 января 2021 года . Проверено 22 января 2021 г.
- ^ Перейти обратно: а б Нейлор, Майк (2011). «Абакаба! – Использование математической модели для соединения искусства, музыки, поэзии и литературы» (PDF) . Мосты . Проверено 6 октября 2017 г.
- ^ Перейти обратно: а б с Конли, Крейг (1 октября 2008 г.). Волшебные слова: словарь . Книги Вайзера. п. 53. ИСБН 9781609250508 .
- ^ Халтер-Кох, Франц и Тичи, Роберт Ф.; ред. (2000). Алгебраическая теория чисел и диофантовый анализ , стр.478. В. де Грюйтер. ISBN 9783110163049 .
- ^ Райт, Крейг (2016). Прослушивание западной музыки , стр.48. Cengage Обучение. ISBN 9781305887039 .
Внешние ссылки
[ редактировать ]- Нэйлор, Майк: abacaba.org
![Треугольник Серпинского[1][2]: АБАКАБА](http://upload.wikimedia.org/wikipedia/commons/thumb/b/bb/ABACABA_Sierpinski_triangle.svg/180px-ABACABA_Sierpinski_triangle.svg.png)
![Линейка,[1][2] исключая 1 и 2: ABACABADABACABA исключая 2: EABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/7/7d/Measuring_-_Fractions_of_an_inch.svg/180px-Measuring_-_Fractions_of_an_inch.svg.png)
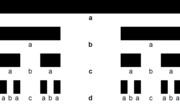
![Бинарное дерево[1][2]/перевернутое генеалогическое древо: ABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e6/Ex_001.png/180px-Ex_001.png)
![Кривая Коха:[1] '"`UNIQ--postMath-00000001-QINU`"' — это ABA, '"`UNIQ--postMath-00000002-QINU`"' — это ABACABA и '"`UNIQ--postMath-00000003 -QINU`"': АБАКАБАДАБАКАБА](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1a/KochCurve1_abacaba_pattern.png/125px-KochCurve1_abacaba_pattern.png)



![Иерархия показателей: ABACABADABACABA[a]](http://upload.wikimedia.org/wikipedia/commons/thumb/a/ad/Solfege_subdivision_de_la_ronde_a_la_croche.svg/180px-Solfege_subdivision_de_la_ronde_a_la_croche.svg.png)
![Уровни показателей:[1] EABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/8/82/Metric_levels.svg/180px-Metric_levels.svg.png)
![Лестница, построенная из максимально возможных квадратов/кубов, но допускающая ступеньки одинакового размера: ABACABADABACABA[1]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/db/Staircase_of_largest_squares_abacaba_pattern.svg/180px-Staircase_of_largest_squares_abacaba_pattern.svg.png)
![«Круговой фрактал»[1] наложен на квадратный фрактал 2 × 2: ABACABADABACABA.](http://upload.wikimedia.org/wikipedia/commons/thumb/7/72/Circle-box_fractal_abacaba_pattern.svg/180px-Circle-box_fractal_abacaba_pattern.svg.png)
![Ханойская башня[1] с четырьмя дисками: ABACABADABACABA.](http://upload.wikimedia.org/wikipedia/commons/thumb/2/20/Tower_of_Hanoi_recursion_SMIL.svg/120px-Tower_of_Hanoi_recursion_SMIL.svg.png)


![3-битный код Грея, визуализируемый как обход вершин куба (0,1,3,2,6,7,5,4):[1] ABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/4/4f/Blue_cube_with_Gray_code_path.png/171px-Blue_cube_with_Gray_code_path.png)
![Замок Шамбор: АБАКАБА[6]](http://upload.wikimedia.org/wikipedia/commons/thumb/4/47/Chambord_Castle_Northwest_facade.jpg/180px-Chambord_Castle_Northwest_facade.jpg)
![Код Грея вдоль числовой линии[1] (OEIS: A003188): ABACABADABACABAEABACABADABACABA](http://upload.wikimedia.org/wikipedia/commons/thumb/b/bd/Gray_code_number_line_arcs.svg/180px-Gray_code_number_line_arcs.svg.png)
![Игла дьявола: [1] ФРИКИРЫ](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Baguenaudier.svg/180px-Baguenaudier.svg.png)




